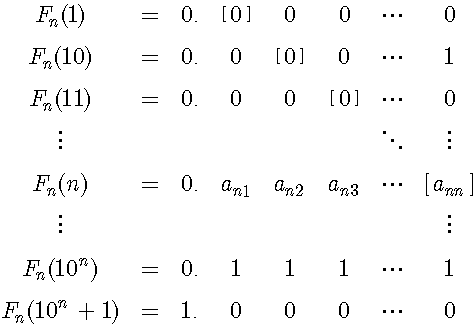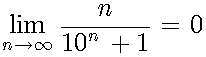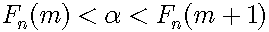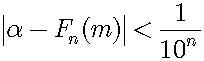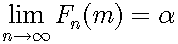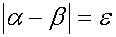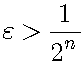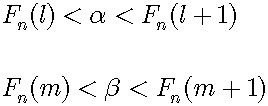An Objection to Cantor's Diagonal Argument
Summary
We shall use the binary number system in this knol except last two sections. Cantor's diagonal procedure cannot apply to all n-bit binary fractions in the interval [0,1]. The number of them is 10n+1. However, the diagonal number differs from only n of them because it is the n-bit binary fraction. As n increases, then the ratio n/(10n+1) is monotonically decreasing. Therefore, no matter how large n is, we cannot apply diagonal procedure to all n-bit binary fractions in the interval [0,1]. Furthermore, according to the pigeonhole principle, the number of irrational numbers is not larger than that of them .
Cantor's Diagonal Proof
Cantor's diagonal argument is a proof devised by Georg Cantor to demonstrate that the real numbers are not countably infinite. Suppose that all real numbers in the section from 0 to 1 are shown by infinite binary fractions, and they are put into one-to-one correspondence with all natural numbers. We could then enumerate all real numbers in this interval as a sequence, R
1,R
2,R
3, ... :

In this sequence, anm is the m-th digit of the Rn and diagonal digits are enclosed in square brackets. Consider an infinite binary fraction X =0.b1b2...bn... . We can compose the new number X as follows: if a11 of R1 is 0 then b1 is 1, if a22 of R2 is 1 then b2 is 0, and so on. Finally, we can get the new number X: X differs in the n-th binary place from Rn. So this new number X is not in our sequence. In conclusion, the assumption, that all real numbers in the interval [0,1] are put into one-to-one correspondence with all natural numbers, must be false. Then, all real numbers between 0 and 1 is strictly larger than all natural numbers. Q.E.D.
The Counterargument Against Diagonal Procedure
Cantor’s diagonal argument uses the completion of infinite processes. However, the mathematicians before Cantor did not accept the completion of infinite processes. This is the controversial point of Cantor’s diagonal argument. To avoid this point, we shall discuss within the range of finite binary fractions. In addition, we shall write numbers in binary notation in equations. First, we enumerate all 11-digit binary fractions in the interval [0,1] in ascending order:
In this sequence, F11(m) is the m-th 11-digit binary fraction and diagonal digits are enclosed in square brackets. Using Cantor’s diagonal procedure, we can compose the number X = 0.111, which differs from the diagonal number in each digit. However, X is different from only the first three numbers in this sequence and then X equals to F11(1000).
Next, we enumerate all n-bit binary fractions in the interval [0,1] in ascending order:
In this sequence, Fn(m) is the m-th n-bit binary fraction and diagonal digits are enclosed in square brackets. We compose the number X in the above mentioned manner. However X differs from only first n numbers in this sequence. This sequence contains X because it includes all n-bit binary fractions in the interval [0,1].
Next, the diagonal number is only n-bits after the binary point. On the contrary, this sequence contains 10n+1 binary fractions. The ratio n/(10n+1) is monotonically decreasing. As n increases, n/(10n+ 1) approaches 0:
Therefore, Cantor's diagonal argument has no application to all n-bit binary fractions in the interval [0,1].
Approximation of Real Numbers
Consider a real number α in the interval [0,1]. If α is not a binary fraction, then α lies between two n-bit binary fractions and there exists a natural number m:
We can approximate the real number α by Fn(m) and then the error is less than 1/10n:
As n increases, then Fn(m) approaches α
At the time, the number of all n-bit binary fractions in the interval [0,1] is consistently 10n+1. No matter how large n is, 10n+1 is a natural number. In conclusion, all n-bit binary fractions in the interval [0,1] are constantly countable.
Where Is Cantor's Paradise?
We shall use decimal notation in last two sections. Consider the sequence of all 150-digit binary fractions in the interval [0,1]. Our sequence consists of approximately 1.4X10
45 binary fractions. Let us compare this number with the diameter of the observable universe. We choose the diameter of a proton as the reference length for measuring the diameter of the observable universe. The ratio of
the diameter of the observable universe to
the diameter of a proton is roughly 2.6X10
41. Even if we could use proton sized digits, we could not write our sequence in one column in our observable universe. At the time, the diagonal number differs from only 150 binary fractions of our sequence. This means that Cantor's diagonal argument cannot apply in our observable universe. Where is Cantor's paradise?
The Pigeonhole Principle
Next, we shall compare the number of irrational numbers with that of binary fractions in the interval [0,1]. Let us regard an irrational number as a pigeon and an interval of adjacent two n-bit binary fractions as a pigeonhole. According to the
pigeonhole principle, if the number of irrational numbers were larger than that of binary fractions, there would be at least two irrational numbers, between which there is no binary fraction. However, there is not such a pair of irrational numbers. The proof is as follows. Consider arbitrary two irrational numbers α and β in the interval [0,1]. If the difference of them is zero, they are the same number. If they are different numbers, the difference isn't zero. Let us assume that the difference is ε:
There exists a natural number n such that:
For enough large n, there are two natural numbers l and m such that:
So, we can sandwich any two irrational numbers by different pairs of n-bit binary fractions. According to the pigeonhole principle, the number of irrational numbers is not larger than that of binary fractions in the interval [0,1]. Evidently, they are countable. Therefore, irrational numbers in the interval [0,1] are countable.
However, there are infinite irrational numbers between two adjacent n-bit binary fractions. We shall consider this problem from the standpoint of the potential infinity. If Aristotle lived now, he would say "There aren't infinite irrational numbers but there is the possibility of the existence of irrational numbers". Let us consider the number line. An irrational number corresponds to a point on the number line. Because the point has no magnitude, anyone cannot detect it. That is, it isn't actually exist. If we want to actualize it, we must locate it on the number line. Hence, it is actualized when it is sandwiched between two n-bit binary fractions. Needless to say, actualized irrational numbers are countable.
Table of Contents