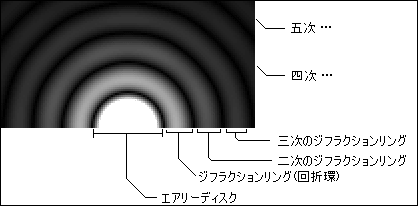
理想的な焦点像を強拡大すると、円盤状の星像(エアリーディスク)と、その周囲に淡い、何層かのリングが伴います。
この環のことをジフラクション(回折)リング(環)と呼びます。
2006/06/30
|
|
 理想的な焦点像を強拡大すると、円盤状の星像(エアリーディスク)と、その周囲に淡い、何層かのリングが伴います。 この環のことをジフラクション(回折)リング(環)と呼びます。 2006/06/30
|
まさかジフラクションリングは『開口部で光が裏側に回り込んだ光だ』なんて、思っていませんよね? ジフラクションリングは、 口径絞りの裏に回り込んだ回折光ではありません。 口径絞りで起こる回折光によって起こります。 2つの文章は、全く同じ意味のようですが、全然違います。 2006/06/30
|
教科書によれば、遮蔽物の裏に波が回り込むのが回折という現象ということになっています。これは、ある意味正解ですが、遮蔽物の裏に波が回り込む部分だけに着目してしまうと誤解を招きます。 この図は、幅広スリットを通り抜ける波の様子を描いています。 その様子を実際に描くには、円形に波が広がる波源をスリット上にびっしりと並べます。 その「円形に波が広がる波源」一つ一つを素源波といいます。 そして、無数の素源波を重ね合わせた結果、すなわち干渉させた結果、光線とは違う向きに進む波が現れることがあります。それを回折と呼びます。 無数の素源波の重ね合わせないと=干渉させないと、回折の様子はわかりません。 2006/06/30
|
これは、理科の教科書でよくみかける、2つの波源(同位相)の干渉の様子です。 教科書では、この後に、波が強めあう条件、波が弱めあう条件といった話が続くのですが、今回はその話ではありません。 今、本当に知りたいのは焦点での波の干渉の様子です。 実際の計算は、計算量が膨大ですが、基本的に2波干渉の応用にしか過ぎません。 つまり、この波源(素源波)がもっとたくさんあったらどうでしょうか?――ということ。 2006/06/30
|
|
そこで、波源を円弧状にずらーっと並べて、同位相で波を起こしてみます。 すると、こんな感じになります。 
円弧の中心部分(焦点)は、波源から等距離になるため波が非常に強くなります。この波が非常に強くなっている部分が、ある程度の太さになっていることに注目してください。 これの輪切りがエアリーディスクです。 そして、焦点には波が斜めに重なりあうため、エアリーディスクを形成している波の周囲に1/2波長ずつズレた淡い波が交互に現れています。 これの輪切りがジフラクションリングになります。 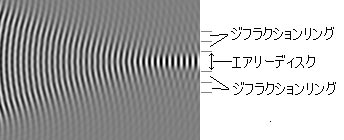  2006/06/30
|
|
[戻る] |