1mmの物体が100mmに拡大されて見えたら100倍、という計算です。
顕微鏡は、観察しようとする物体の実寸がわかっているので、このような方法が使えます。
天体望遠鏡の倍率は、角倍率と言います。
仮に、月の実視直径が0.5度のとき、望遠鏡で拡大したら50度に見えたとします。この場合、50度÷0.5度=100倍、となります。
肉眼で見た角度と、拡大したときの見かけの角度の比が望遠鏡の倍率(角倍率)です。

2014/05/04
|
|
|
天体望遠鏡の倍率を求める式。 望遠鏡の倍率 = 対物レンズの焦点距離 ÷ 接眼レンズの焦点距離 です。 なぜか、割算です。 なぜ焦点距離を焦点距離で割って倍率が求まるのでしょうか? 2014/05/04
|
|
顕微鏡の倍率は、横倍率と言います。明視距離(25cmの距離)で見た時の大きさに対して何倍に拡大されているか、です。 1mmの物体が100mmに拡大されて見えたら100倍、という計算です。 顕微鏡は、観察しようとする物体の実寸がわかっているので、このような方法が使えます。 天体望遠鏡の倍率は、角倍率と言います。 仮に、月の実視直径が0.5度のとき、望遠鏡で拡大したら50度に見えたとします。この場合、50度÷0.5度=100倍、となります。 肉眼で見た角度と、拡大したときの見かけの角度の比が望遠鏡の倍率(角倍率)です。  2014/05/04
|
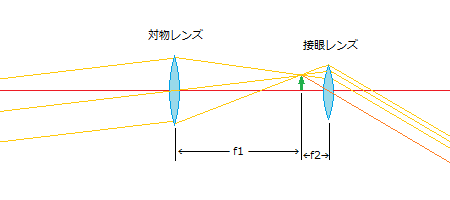 天体望遠鏡は、遠方から来る光を対物レンズによって一度焦点に結像させ、焦点にできた像を接眼レンズという名のルーペで拡大する仕組みです。 光を追って説明すると、対物レンズで焦点に一度結像され、焦点を通り過ぎて拡散していく光を接眼レンズ側で受けて平行光束にして(無限遠投影するように)射出する構造をしています。 ピントが合っている状態の望遠鏡では、対物レンズと接眼レンズは焦点を共有しているところがポイントです。 2014/05/04
|
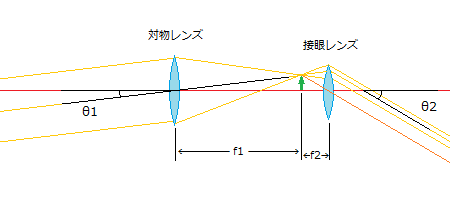 肉眼で見た角度(θ1)と、拡大したときの見かけの角度(θ2)の比が望遠鏡の倍率(角倍率)です。 よって、望遠鏡の倍率は、 倍率=θ2÷θ1 で求めることができます。 厳密には、θ1が伏角(水平より下の角度=符号がマイナス)、θ2が仰角(水平より上の角度=符号がプラス)なので、倒立像になる場合の倍率はマイナスになるのですが、便宜的にプラス扱いします。 さて、このままでは、関係がよくわからないので、θ2を接眼レンズの中心を通るように平行移動します。 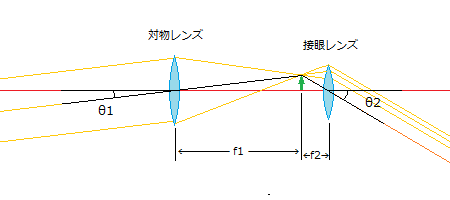 黒い線だけ抜き出して整理すると、焦点上の像の高さをh、対物レンズの焦点距離をf1、接眼レンズの焦点距離をf2とした場合、 tan θ1=h/f1 tan θ2=h/f2 と書き表すことができます。 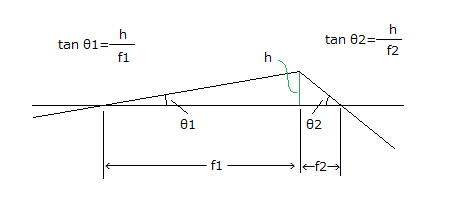 天体望遠鏡そのものの倍率は近軸領域で求めるので、 tan θ1=h/f1 tan θ2=h/f2 は、 θ1=h/f1 θ2=h/f2 と置き換えることができます。 望遠鏡の倍率は 倍率=θ2/θ1 ですから、それぞれθ1,θ2に代入して整理すると 倍率=(h/f2)/(h/f1) =f1/f2 = 対物レンズの焦点距離 ÷ 接眼レンズの焦点距離 となります。 2014/05/04
|
|
[戻る] |