�M�̈ړ��ƔM��R�A���M�̂܂Ƃ߁i�K�v�ȕ��M��̌v�Z�܂Łj
�g�����W�X�^��R�[�q���M�����[�^���g�p����ہA����d�͂������ƕ��M�ɂ��čl����K�v���o�Ă��܂��B
�E���M��͕K�v���s�v��
�E���M��͉���I��悢���B
�Ȃǂ��l���Č��肵�Ȃ���Ȃ�܂���B
�M�҂̏ꍇ�A���M��K�v�Ƃ��邱�Ƃ��p�ɂɂȂ��̂ŁA�ǂ̂悤�ɍl����̂���Y�ꂪ���ł��B�v�Z�菇 �͊o���Ă���̂ł����A�S�z�ɂȂ��Ē��ׂȂ������肵�Ă��܂��܂��B���ׂȂ����̂��A�������������� �{����������o���Ă����肷��̂ňӊO�Ƒ�ςł��B�Ȃ̂ō��̃y�[�W�Ƀ����Ƃ��Ă܂Ƃ߂Ă������Ǝv���܂��B
�P�D�M�ɂ���
�����ł́A�g�����W�X�^��R�[�q���M�����[�^�Ȃǂ̕��M���l����Ƃ��ɕK�v�ƂȂ�u�M�v�ɂ��Ă̍l�������܂Ƃ߂܂��B
�P�|�P�D���M�v�ɂ�����u�M�v�ɂ��Ă̌��
���퐶���̉�b�̒��Łu�M������v�Ƃ��u�M���v��v�Ƃ������\�����g�����Ƃ�����܂��B�����b�̒��ł�
����ł悢�̂ł����A���M�v�Łu�M�v�Ƃ������t���g���Ƃ��A�����悤�ɂ͎g���܂���B
�@���퐶���ł́u�M������v�Ƃ������t�́u���x�������v�Ƃ����Ӗ��ł��B�u�M���v��v�Ƃ������t���u���x���v��v
�Ɠ����Ӗ��Ŏg���Ă��܂��B�܂�A�u�M�v�Ɓu���x�v���Ӗ��Ŏg�p���Ă���̂ł��B
���M�v�Ō����u�M�v�̓G�l���M�[���Ӗ����܂��B�Ȃ̂ō����E�Ⴂ�Ƃ����\���͎g���܂���B�������Ⴂ����\�� ����̂͂����܂ł����x�ł��B
�P�|�Q�D�M�̗�
�u�M�v�̓G�l���M�[�Ƃ��Ă̗ʂ��u�M�ʁv�Ƃ��ĕ\�����Ƃ��ł��܂��B�P�ʂ̓W���[��[J]�A���邢�̓J�����[[cal] ���g���܂��B���̃y�[�W�ł̓W���[��[J]��p���ĕ\���܂��B
�P�|�R�D�M�e��
���镨�̂̉��x���P[��]�グ��̂ɕK�v�ȔM�ʂ�M�e�ʂƌ����܂��B�P�ʂ̓W���[�����ێ��x[J/��]���g���܂��B
�@�Ⴆ�A�M�e�ʂP�O[J/��]�̕��̂̉��x���T[��]�����悤�Ǝv������A�K�v�ȔM��Q[J]��
�@�@Q[J]���P�O[J/��]�~�T[��]���T�O[J]
�ƁA���܂�܂��B�܂��A�������̂ɔM�ʂW[J]��^�����牽�x�オ�邩��
�@�@T[��]���W[J]/�P�O[J/��]���O�D�W[��]
�Ƌ��܂�܂��B
���̂悤�ɁA���̂̔M�e�ʂƔM�A���x�݂͌��ɊW�������Ă��܂��B
�P�|�S�D���M
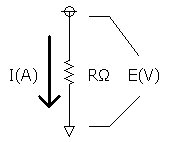
�d�C��H�ł́A��R�ɓd���𗬂��Ɠd�͂�����܂��B���̏���ʂ͒�R�ɂ������d���Ɨ��ꂽ�d�����������l�ŕ\�����
����d�͂ƌĂ�܂��B����d�͂͒�R����M�ƂȂ��ĕ��o����܂��B
�@����͒�R�ɂ���āA�d�C�G�l���M�[���M�G�l���M�[�ɕϊ�����Ă��邱�Ƃ��Ӗ����Ă��܂��B�ϊ��Ɠ����ɒ�R
�Ƃ������̂ɔM�G�l���M�[�����������̂ŁA���g�̔M�e�ʂƂ̊W�Œ�R�̉��x�͏オ��܂��B
|
�@�}�P�Ɏ����悤�ɁAPe[W]�̓d�͂�����ꂽ�ꍇ�A���̃G�l���M�[�̑S�Ă��M�G�l���M�[Pt[W]��
�ϊ�����܂��B �@�@�@�M�G�l���M�[Pt[W]������d��Pe[W] �����Ŏg���Ă���M�G�l���M�[�̒P�ʃ��b�g[W]�́A�d�����Ƃ��ăW���[�����b[J/s]�Ƃ��čl���邱�Ƃ� �ł��܂��B�܂�A�P�b�ԂɔM��Pt[J]����������ƍl���邱�Ƃ��ł���̂ł��B ��R�̔M�e�ʂ�Cr[J/��]�ł���Ƃ���ƁA�P�b���Ƃ̉��x�㏸��Tr[��]�� �@�@�@��Tr[��]��Pt[J]/Cr[J/��] �ɂȂ�܂��B �@�M�e�ʂƔM�̊W�����������Ƃ��A�d���𗬂����܂܂ɂ���ƂP�b�Ƀ�Tr[��]�̃y�[�X�ʼni���ɉ��x�㏸�𑱂��܂��B |
�P�|�T�D�M�̈ړ�
�u���M�v�̍��ŁA�u��R�ɓd���𗬂�������ƒ�R�̉��x�͉i���ɏオ�葱����v�Əq�ׂ܂������A���ۂ�
�����͂Ȃ�܂���B����͔M�̈ړ����s���Ă��邩��ł��B
�@���x���������̂ƒႢ���̂�����Ƃ��A���x���������̂���Ⴂ���̂ɔM���ړ����܂��B�����M�̈ړ��ƌ����A
���x���Ⴂ���͈̂ړ����Ă����M�ʂ̕��������x���㏸���A���x���������͎̂������M�ʂ̕��������x���������
���B���̌��ۂɂ��A���x���������̂ƒႢ���͓̂������x�ɂȂ낤�Ƃ��܂��B
�@��L�̒�R�̗�ł́A��R�̉��x�������Ȃ������߁A���x���Ⴂ��R�̎���̋�C�ɔM���ړ��������ƂɂȂ�܂��B
�@�M���ړ�����ʂ́A�M��Q[W]�Ƃ��ĕ\�����܂��B�P�ʂ�[W]�͂P�b�Ԃɗ����M�ʂƂ���[J/s]��\���Ă��܂��B
�P�|�U�D�M��R�̑���
���i�A��i�d�͓��Ŏg�p���Ă����R�͏Ă��ł��܂���B��R�������̋�C�ւƔM�̈ړ����s���Ă��邩��ł��B �ł́A��i�d�͈ȏ�Œ�R���g�p����Ƃǂ��Ȃ邩�B��R�͏Ă��ł��Ă��܂��܂��B
��i�d�͈ȏ�Œ�R���g�p����Əł��Ă��܂��̂́A�u����̋�C�Ɉړ�����M�v�����u�d�͏���ɂ����
���������M�v�̕�����������Ȃ̂ł��B���������M���������߁A��R�����̔M�ʂ͂ǂ�ǂ��ĉ��x���オ��A
�������g���Ă��Ă��܂��̂ł��B
�@�u����̋�C�Ɉړ�����M�v�����u�d�͏���ɂ���ċ��������M�v�̕��������Ƃ�����Ԃ��Ȃ����݂���̂�
�Ƃ����ƁA�����ɂ͔M�̈ړ������ɂ�������M��R��[��/W]�Ƃ������̂����݂��邩��Ȃ̂ł��B�M��R�Ƃɂ����
�M�̈ړ��ʂ���������Ă���̂ł��B
�M�̈ړ����n�܂�ɂ́A���̊Ԃʼn��x�����K�v�ł��B���̊Ԃ̉��x������T[��]�ŁA�M��Q[W]�����������Ƃ��܂��B
���̂Ƃ��̔M�̗���ɂ����ł���M��R��[��/W]�͎��̎��ŋ��߂邱�Ƃ��ł��܂��B
�@�@�@��[��/W]����T[��]/�M��Q[W]�@�E�E�E�E���P
�P�|�V�D�M���|���x���@����
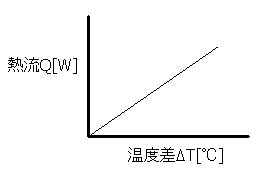
���P��M�������߂鎮�ɕό`����Ǝ��Q�̂悤�ɂȂ�܂��B
�@�@�@�@�M��Q[W]����T[��]/��[��/W]�@�E�E�E�E���Q
�����āA��[��/W]�����ł���Ƃ���Ɛ}�Q�̂悤�ȃO���t�������܂��B
���̃O���t����A���x�����傫���Ȃ�ƔM���������Ȃ��Ă������Ƃ�������܂��B
|
|
�����ŁA�d�C��R�̉��x�㏸���l���Ă݂܂��傤�B
�@�d�C��R�ɓd���������ēd���𗬂��ƁA����d�͂��M�ɕϊ�����ēd�C��R�̎��M�ʂ������܂��B
�@�������M�ʂɂ���ēd�C��R�̉��x���オ��܂��B
�A����̋�C�������x���オ��ƔM�����������܂��B�M������������Ə���d�͂Ŕ�������M������̋�C��
�@������̂ŁA��R�����ɒ~�ς����M�ʂ�[����d�́|�M��]�ƂȂ��ć@�̂Ƃ���菭�Ȃ��Ȃ�܂��B
�B�������M��[����d�́|�M��]�ɂ���Ē�R�̉��x���オ��܂��B
�C����̋�C�Ƃ̉��x�����J���̂ŁA�M���������܂��B
�D�@�B�ƇC���J��Ԃ��āu����d�́��M���v�ɂȂ�ƁA��R�����̔M�ʂ������Ȃ��Ȃ�̂Œ�R�̉��x�͏㏸���Ȃ��Ȃ�܂��B
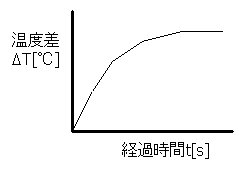
���̗l�q��}�R�Ɏ����܂��B
����d��P[W]�ƔM��Q[W]���������Ȃ�Ƃ��̉��x���́A���P�����̂悤�ɕό`���邱�Ƃŋ��߂邱�Ƃ��ł��܂��B
�@�@�@��T[��]����[��/W]�~����d��P[W]�@�E�E�E�E���R
���ɓd�C��R�̔M��R���Ɓ��P�O�O[��/W]�A����d��P���P[W]�Ƃ���ƃ�T���P�O�O[��]�ƂȂ��āA���͉��x�ƂP�O�O��
�̉��x���ł���ȏ㉷�x�͏オ��Ȃ��Ȃ�܂��B
���̂悤�ɔM������ȏ゠����Ȃ��Ȃ�����Ԃ����ԂƌĂт܂��B�܂��A����ԂɎ���܂ł̉��x�㏸���Ă���
��Ԃ��ߓn��ԂƌĂт܂��B
�@�d�q���i�Ƃ��̎���̋�C�Ƃ̊Ԃ̔M��R�Ƃ�������A����d�͂ɑ������Ԃ̉��x�����v�Z�ŋ��߂邱�Ƃ�
�ł���悤�ɂȂ�܂��B�i����d�͂ɑ��ĉ��x�܂ʼn��x���オ��̂���������悤�ɂȂ�܂��B�j���̃y�[�W�̎��
�ł���g�����W�X�^��R�[�q���M�����[�^�̕��M�������ł��B���͂̋�C�ɑ���M��R�Ƃ����߂邱�Ƃɂ���āA
�E���M�͑���Ă���̂�
�E�ǂ̂悤�ɂ���Ε��M�������悤�ɂȂ�̂�
���l���邱�Ƃ��ł���悤�ɂȂ�̂ł��B
�܂Ƃ߂Ƃ��Ď��̗���l���Č��܂��傤�B
���͂̋�C�ɑ���M��R�Ƃ��P�O�O[��/W]�A�P�Q�O[��]����Əł��n�߂�d�C��R�ŁA�C���S�O[��]�ɂ�����
����ł���ő�d�͂��v�Z���Ă݂܂��傤�B
�@�@�@�@�@���͂̋�C�ƒ�R�̉��x����T��120[��]�|40[��]��80[��]
�@�@�@�@�@����d��P[W]���M��Q[W]��80[��]/100[��/W]��0.8[W]
�ƂȂ�܂��B
����d�͂�0.8[W]�̂Ƃ��ɓd�C��R�̉��x��120[��]�̒���ԂɂȂ�܂��B����d�͂�0.8[W]����ƒ���Ԃ�
���x��������̂ŁA�d�C��R�̉��x�͏㏸����120[��]���ďł��n�߂܂��B
�P�|�W�D�M��H
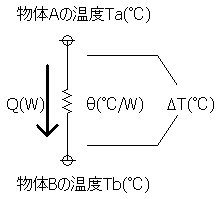
���̊Ԃ̉��x���A�M���A�M��R�̊W�́A�d�C��H�̂悤�ɒ��ۉ����ĔM��H�Ƃ��čl���邱�Ƃ��ł��܂��B
�@���̗l�q��}�S�Ɏ����܂��B
|
���x���F��T(��) �M���@�FQ(W) �M��R�F��(��/W) ��T=Q�� ��=��T/Q Q=��T/�� �E�M��R�ƂɔM��Q�������ƁA�Ƃ̗��[�ɂ͉��x��T��������B �E�M��R�Ƃɉ��x����T��������ƁA�M��Q�������B |
�Q�D�����̃p�b�P�[�W�ł̔M��R�����߂�
�u�P�D�M�ɂ��āv�ł́A�d�q���i�̔M��R�A���M�ʁA����Ԃ̉��x���̊W���킩��܂����B
�@�����ł́A�����̂̃p�b�P�[�W�̒��Ń`���l�������M���Ă���A���̔M���O�C�i���͂̋�C�j�ɗ���Ă����o�H��
�M��R�̋��ߕ����q�ׂ܂��B
�@�`���l���Ŕ��������M�͂ǂ�ȏꍇ�ł��ŏI�I�ɂ͊O�C�ɕ��o����܂��B�Ȃ̂Ń`���l���|�O�C�Ԃ̔M��R��
������A�u���M�ʂ������Ԃ̉��x���v�u����Ԃ̉��x����g�p�\�Ȕ��M�ʂ��v�Ǝ��R�Ɍv�Z�ł���悤
�ɂȂ�܂��B�����ɍő��i���x�Ǝg�p����O�C�̉��x�͈͂���������u���M�킪�K�v���ǂ����v�u�K�v�ȕ��M���
�M��R�̒l�́v�Ƃ������Ƃ��Z�o���邱�Ƃ��ł��܂��B
�Q�|�P�D�p�b�P�[�W���̔��M�ƔM�̈ړ�
���M���镔���̓`���l���Ƃ��W�����N�V�����Ƃ��Ă�Ă��܂��B���i�̎�ނ�[�J�[�ɂ���Ă��Ăѕ���
�F�X�ł����A�����ł̓`���l���ƌĂԂ��Ƃɂ��܂��B
�@�`���l���̉��x�͍ő��i�����߂��Ă���A���M��ł͂��̉��x���ő��i���Ȃ��悤�ɂ��邱�Ƃ��ړI
�ɂȂ�܂��B
�`���l���ɓd�͂̏������ƁA�`���l���̔M�e�ʂƔ�������M�ɂ���ă`���l���̉��x���オ��܂��B ����ƁA�`���l���ƃP�[�X�Ԃɉ��x���������ăP�[�X�ɑ��ĔM�̈ړ����n�܂�܂��B
�Q�|�Q�D�`���l���|�P�[�X�ԔM��R��ch-c
�`���l���ƃP�[�X�̊Ԃɂ͔M��R��ch-c�����݂��܂��B���̒l�̓f�[�^�V�[�g�ɋL�ڂ���Ă���ꍇ������܂��� �L�ڂ���Ă��Ȃ��ꍇ�ɂ͌v�Z�ŋ��߂邱�Ƃ��ł��܂��B
|
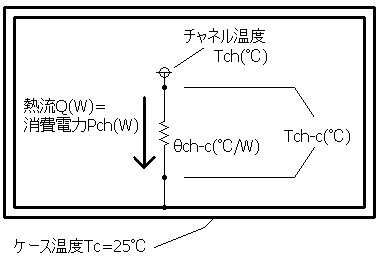
�@�f�[�^�V�[�g�Ƀ`���l���|�P�[�X�ԔM��R��ch-c�̒l���L�ڂ���Ă��Ȃ��Ƃ��ɂ́A
�f�[�^�V�[�g�̍ő��i�̂Ƃ���ɋL�ڂ���Ă����̒l����v�Z���ċ��߂܂��B �@���e����Pch(W)�F�P�[�X���xTc���Q�T���ƈꏏ�ɋL�ڂ���Ă��܂��B �A�ő�`���l�����xTch(��) �u�P�[�X���x��25���ɕۂ�����ԂŁA�`���l�����x���ő�`���l�����xTch�Œ���ԂɂȂ� ����d�͂͋��e����Pch�ł���v�Ɖ��߂��܂��B ���̏�Ԃ�}�Ŏ������̂��}�T�ł��B |
�`���l���|�P�[�X�ԉ��x��Tch-c[��]���ő�`���l�����xTch(��)�|�Q�T[��]
�Ƃ���ƁA�`���l���|�P�[�X�ԔM��R��ch-c�����߂鎮�͈ȉ��̂悤�ɂȂ�܂��B
�@�@�@�@��ch-c[��/W]��Tch-c[��]/Pch[W]
�Q�|�R�D���i�P�̂̃`���l���|�O�C�ԔM��R��ch-a
���i�P�̂̃`���l���|�O�C�ԔM��R��ch-a��������ƁA���M����g�p���Ȃ����̔M�������v�Z���邱�Ƃ��ł��܂��B
�@��ch-a�̒l�̓f�[�^�V�[�g�ɋL�ڂ���Ă���ꍇ�Ƃ��Ȃ��ꍇ������܂��B�L�ڂ���Ă��Ȃ��Ă��A�O�C���x
�ɑ��鋖�e�d�͂��f�[�^�V�[�g�ɍڂ��Ă���ΎZ�o���邱�Ƃ��ł��܂��B���̒l���f�[�^�V�[�g�ɂȂ��ꍇ�ɂ�
���ۂɃP�[�X���x�𑪒肵�ĎZ�o���邱�ƂɂȂ�܂��B
�����ł����A���ł̏ꍇ�A�f�[�^�V�[�g�ɋL�ڂ���Ă��邱�Ƃ������ł��B
�@Renesas�̓h�L�������g�ɋL�ڂ���Ă���̂��������̂Ō�q�̕\�T�ɍڂ��Ă����܂����B
�Q�|�R�|�P�D�O�C���x�ɑ��鋖�e�d�͂�������ꍇ
|
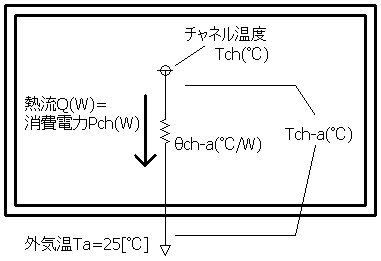
�@�v�̂͂Q�|�Q�D�`���l���|�P�[�X�ԔM��R��ch-c�Ɠ����ł��B�������A���e����Pch�̒l�͊O�C���xTa��25����
���̃f�[�^���g�p����K�v������܂��B���̒l���f�[�^�V�[�g�ɏo�Ă��邩�ǂ����͐��i�������ł��B �@�v�Z�Ɏg���f�[�^�͈ȉ��̓�ł��B �@���e����Pch(W)�F�O�C���xTa��25���ƈꏏ�ɋL�ڂ���Ă��܂��B �A�ő�`���l�����xTch(��) ���e�����ƍő�`���l�����x�͎��̂悤�Ɍ��т��čl���܂��B �u�O�C���x��25���ɕۂ�����ԂŁA�`���l�����x���ő�`���l�����xTch�Œ���ԂɂȂ� ����d�͂͋��e����Pch�ł���v�Ɖ��߂��܂��B ���̏�Ԃ�}�Ŏ������̂��}�U�ł��B |
�`���l���|�O�C�ԉ��x��Tch-a[��]���ő�`���l�����xTch(��)�|�Q�T[��]
�Ƃ���ƁA�`���l���|�O�C�ԔM��R��ch-a�����߂鎮�͈ȉ��̂悤�ɂȂ�܂��B
�@�@�@�@��ch-a[��/W]��Tch-a[��]/Pch[W]
�Q�|�R�|�Q�D�O�C���x�ɑ��鋖�e�d�͂�������Ȃ��ꍇ
|
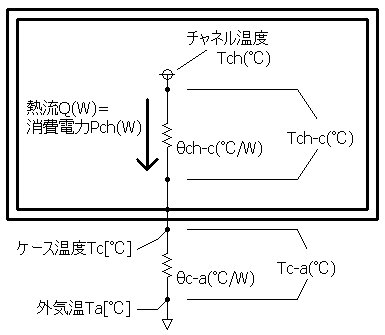
�@���̏ꍇ�A�f�[�^�V�[�g����̒l�ŎZ�o����͖̂����Ȃ̂ŁA�P�[�X�̉��x���v������
�v�Z����K�v������܂��B �@�`���l���|�O�C�ԔM��R��ch-a�́A�`���l���|�P�[�X�ԔM��R��ch-c�ƃP�[�X�|�O�C�ԔM��R��c-a �𑫂������̂ƍl���邱�Ƃ��ł��܂��B���̏�Ԃ�}�V�Ɏ����܂��B �@�`���l���|�P�[�X�ԔM��R��ch-c�̓f�[�^�V�[�g����̒l���g���āA�Q�|�Q�Ŏ��������@�� �l���Z�o���邱�Ƃ��ł��܂��̂ŁA�P�[�X�|�O�C�ԔM��R��c-a���v���ɂ���Ēl�����߂邱�ƂɂȂ�܂��B |
�P�[�X���xTc�ƊO�C���xTa���v�����Ȃ���A����d��Pch��납�瑝�₵�Ă䂫�A�P�[�X�ƊO�C���̍�
�iTc��Ta�̍��j�ƁA���̂Ƃ��̏���d��Pch���g���Čv�Z���邱�Ƃ��ł��܂��B
���̂Ƃ����ӂ��ׂ��_�́A
�E����d�͂�ω������Ă������ԂɂȂ�܂łɏ������Ԃ�������܂��B
�@����d�͂�ω������Ă���P�[�X�̉��x�����肷��܂ő҂��Ƃ��K�v�ł��B
�E�`���l�����x���ő��i���Ȃ��͈͂ōs��Ȃ���Ȃ�܂���B
�@�`���l���|�P�[�X�ԔM��R��ch-c�����炩���ߎZ�o���āA�����\�ȃP�[�X���x��
����d�͂̊W��c�����Ă����܂��傤�B
�P�[�X�|�O�C�ԉ��x��Tc-a[��]���P�[�X���xTc(��)�|�O�C���xTa[��]
�Ƃ���ƁA�P�[�X�|�O�C�ԔM��R��c-a�����߂鎮�͈ȉ��̂悤�ɂȂ�܂��B
�@�@�@�@��c-a[��/W]��Tc-a[��]/Pch[W]
�Q�|�S�D���M��t���`���l���|�O�C�ԔM��R��ch-a
���M��Ɏ��t�����ꍇ�̃`���l���|�O�C�ԔM��R��ch-a�́A
�E�`���l���|�P�[�X�ԔM��R��ch-c
�E�P�[�X�|���M��ԔM��R��c-h
�E���M��|�O�C�ԔM��R��h-a
�����v�������̂ɂȂ�܂��B���̗l�q��}�W�Ɏ����܂��B
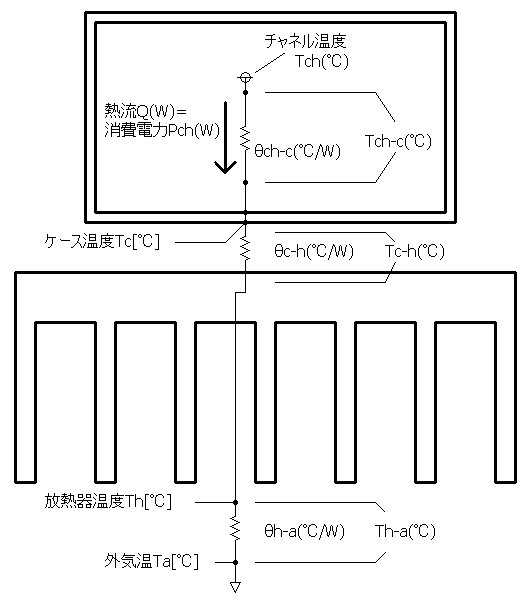 �@�@�@�@��ch-a����ch-c�{��c-h�{��h-a �}�W�D���M��t���`���l���|�O�C�Ԓ�R��c-a |
�`���l���|�P�[�X�ԔM��R��ch-c�̋��ߕ��͂Q�|�Q�̐����Ɠ����Ȃ̂ŁA�����ł̓P�[�X�|���M��ԔM��R��c-h�� ���M��|�O�C�ԔM��R��h-a�ɂ��ďq�ׂ܂��B
�Q�|�S�|�P�D�P�[�X�|���M��ԔM��R��c-h
�P�[�X�|���M��ԔM��R��c-h�́A
�E�P�[�X�ƕ��M��̐ڐG�ʐς܂��̓P�[�X�̌`��
�E�≏�̗L��
�E�V���R���O���X�̗L��
�E���ߕt���g���N
�Ȃǂ��e�����܂��B
���m�ɒm�肽���ꍇ�ɂ͌v�����邵���Ȃ��̂ł����A�����̃��[�J�[���ڈ��ƂȂ�l����Ă���Ă��܂��B
�@�V���R���O���X��≏�͐��i�ɂ���Ă��̓������Ⴄ�̂ŁA�ڈ��ŐS�z�ȏꍇ�ɂ͂�͂�v�����邵������܂���B
���ł�Renesas�̃h�L�������g�Ɂu�P�[�X�|���M��ԔM��R��c-h�v�̃f�[�^���ڂ��Ă����̂ŕ\�S�C�T�Ɏ����܂��B
| �p�b�P�[�W | �≏�� | ��c-h[��/W] | ���ߕt���g���N [N.m] |
|
| �V���R���O���X | ||||
| ���� | �Ȃ� | |||
| TO-220AB | �≏�Ȃ� | 0.3-0.5 | 1.5-2.0 | 0.6 |
| �}�C�J (50-100 ��) | 2.0-2.5 | 4.0-6.0 | ||
| TO-220(IS) | �≏�Ȃ� | 0.4-0.6 | 1.0-1.5 | 0.6 |
| TO-3P | �≏�Ȃ� | 0.1-0.2 | 0.5-0.9 | 0.8 |
| �}�C�J (50-100 ��) | 0.5-0.8 | 2.0-3.0 | ||
| TO-3PL | �≏�Ȃ� | 0.1-0.2 | 0.4-1.0 | 0.8 |
| �}�C�J (50-100 ��) | 0.5-0.7 | 1.2-1.5 | ||
�\�T�DRenesas�@�P�[�X�|���M��M��R�ƒ��ߕt���g���N
| �p�b�P�[�W | �≏�� | ��c-h[��/W] | ��ch-a[��/W] | ���ߕt���g���N [N.m] |
|
| �V���R���O���X | |||||
| ���� | �Ȃ� | ||||
| DPAK | �≏�Ȃ� | 0.3-0.6 | 2.0-2.5 | 178 | 0.6 |
| TO-220AB | �≏�Ȃ� | 0.3-0.5 | 1.5-2.0 | 80 | 0.6 |
| �}�C�J (50-100 ��) | 2.0-2.5 | 4.0-6.0 | |||
| LDPAK | �≏�Ȃ� | 0.3-0.5 | 1.5-2.0 | 83.3 | 0.6 |
| TO-220FM | �≏�Ȃ� | 0.4-0.6 | 1.5-2.0 | 62.5 | 0.6 |
| TO-3P | �≏�Ȃ� | 0.1-0.2 | 0.5-0.9 | 55 | 0.8 |
| �}�C�J (50-100 ��) | 0.5-0.8 | 2.0-3.0 | |||
| TO-3PFM | �≏�Ȃ� | 0.3-0.5 | 1.0-1.5 | 42 | 0.6 |
| TO-3PL | �≏�Ȃ� | 0.1-0.2 | 0.4-0.5 | 45 | 0.8 |
| �}�C�J (50-100 ��) | 0.5-0.7 | 1.2-1.5 | |||
�Q�|�S�|�Q�D���M��|�O�C�ԔM��R��h-a
�s�̕i�̕��M����g���ꍇ�ɂ́A�������[�J�[�̃f�[�^�V�[�g����M��R�ׂ邱�ƂɂȂ�܂��B
�@�����Ő��ĉ��H������������M��Ƃ��Ċ��p������@������܂��B�g�����W�X�^�Z�p����
�����̖ʐςƔM��R�̃O���t���ڂ��Ă���̂ł����A�R�s�[����݂̂͜���̂ŔN���y�[�W
�������ȉ��ɋL���Ă����܂��B
�g�����W�X�^�Z�p�Q�O�O�R�N�S�����P�W�T�y�[�W
�g�����W�X�^�Z�p�Q�O�O�V�N�Q�����Q�R�Q�y�[�W
�R�D�v�Z��
�H���d�q�ł��܂��ܔ����Ă���N�`���l��MOS-FET�A2SK3628�̃f�[�^���g���Ď��Z���Ă݂܂��B
�f�[�^�V�[�g�������ł�
��ő��i��\�U�Ɏ����܂��B
�\�U.�@2SK3628�̐�ő��i
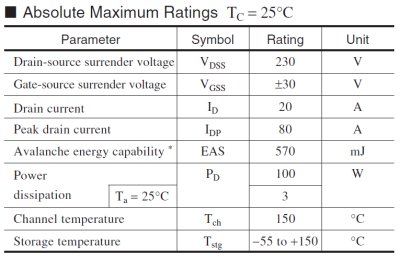
�R�|�P�D�`���l���|�P�[�X�ԔM��R��ch-c
�v�Z�ɕK�v�ȃf�[�^��\�U���甲���o���ƈȉ��̂悤�ɂȂ�܂��B
�@�@�@����d��Pd��100[W]
�@�@�@�`���l�����xTch��150[��]
�`���l���|�P�[�X�ԔM��R��ch-c���i150[��]�|25[��]�j/100[W]��1.25[��/W]
�ƂȂ�܂��B
�R�|�Q�D�`���l���|�O�C�ԔM��R��ch-a
�v�Z�ɕK�v�ȃf�[�^��\�U���甲���o���ƈȉ��̂悤�ɂȂ�܂��B
�@�@�@����d��(Ta��25��)Pd���R[W]
�@�@�@�`���l�����xTch��150[��]
�`���l���|�O�C�ԔM��R��ch-a���i150[��]�|25[��]�j/3[W]��41.7[��/W]
�ƂȂ�܂��B
�R�|�R�D���M��Ȃ��Ŏg���Ƃ��̍ő����d��
���̂e�d�s����M��Ȃ��Ŏg�p����Ƃ��̎g�p�\�ȍő����d�͂����߂Ă݂܂��傤�B
�@�܂��͍ő�`���l�����x����l���܂��傤�B���肬��Őv����ƕ|���̂ŁA����͍ő��i��80��
�ɂ��Ă݂܂��B
�@�@�@�@Tch��150���~0.8��120��
�@���ɊO�C���ł����A�g�p������ł̍ō��C���v���X���ōl���܂��B�^�Ăł�������40���܂ł͂߂�����
�Ȃ�Ȃ��Ǝv���̂ŁA40���Ɂ{10������
�@�@�@�@Ta��50��
�Ƃ��܂��B����Ɖ��x����
�@�@�@�@Tch-a��120���|50����70��
�ƂȂ�܂��B
���Ƃ̓`���l���|�O�C�ԔM��R��ch-a���g����70���̉��x���Œ���ԂɂȂ����d�͂��v�Z����ΏI���ł��B
�@�@�@�@Pch[W]��Tch-a/��ch-a��70[��]/41.7[��/W]��1.68[W]
�R�|�S�D����d��30W�Ŏg������
���M��Ɏ��t���Ȃ���Ԃł�1.7W���x�܂ł����g�p���邱�Ƃ��ł��܂���B������d�͂������p�r��
�g�p����ɂ͕��M��Ɏ��t���ĔM��R�������Ă�����K�v������܂��B
�@�g�p���鉷�x�͂R�|�R�Ɠ���������30W�܂Ŏg�p�ł���M��R���l���Č��܂��傤�B
�܂��A���x�����͂R�|�R�Ɠ����Ȃ̂�
�@�@�@�@Tch��150���~0.8��120��
�@�@�@�@Ta��50��
�@�@�@�@Tch-a��120���|50����70��
�ł��B���̉��x���ŁA30W�̏���d�͂Œ���ԂɂȂ�M��R��ch-a��
�@�@�@�@��ch-a��Tch-a/Pch��70[��]/30[W]��2.33[��/W]
�ƂȂ�܂��B��ch-a�̒l��2.33[��/W]���傫���Ȃ��30W��������Ƃ��̉��x��Tch-a��70������
���܂��܂��̂ŁA
�@�@�@�@��ch-a��2.33[��/W]
�͈̔͂ōl����K�v������܂��B
[�`���l���|�O�C�ԔM��R��ch-a]��[�`���l���|�P�[�X�ԔM��R��ch-c]�{[�P�[�X�|�O�C�ԔM��R��c-a]
�ƍ��킹��ƁA
�@�@�@�@��ch-c�{��c-a��2.33[��/W]
�ƂȂ�A��ch-c��1.25[��/W]�Ȃ̂�
�@�@�@�@1.25[��/W]�{��c-a��2.33[��/W]
�@�@�@�@��c-a��1.08[��/W]
�ƂȂ�܂��B
����ɁA
[�P�[�X�|�O�C�ԔM��R��c-a]��[�P�[�X�|���M��ԔM��R��c-h]�{[���M��|�O�C�ԔM��R��h-a]
�ł��邱�Ƃ���
�@�@�@�@��c-h�{��h-a��1.08[��/W]
�ƂȂ�܂��B
�����ŁA�P�[�X�|���M��ԔM��R��c-h���l����ɂ�����AFET�̕��M��ւ̎��t���������߂܂��B
�E�≏�Ȃ�
�E�V���R���O���X�h�z
�Ƃ��܂��B
Panasonic�̃p�b�P�[�W���Ƃ̐ڐG�M��R�̃f�[�^������ł��Ȃ������̂ŁA�\�S�̓��ł̒l�𗬗p���܂��B
TO-3P�ɐڐG�ʐς��߂��悤�Ȃ̂�
�@�@�@�@��c-h��0.20[��/W]
�Ƃ��܂����B����āA
�@�@�@�@0.2[��/W]�{��h-a��1.08[��/W]
�@�@�@�@��h-a��0.88[��/W]
�ƂȂ�A���M��̔M��R��0.88[��/W]�ȉ��̂��́A�Ƃ������ƂɂȂ�܂��B