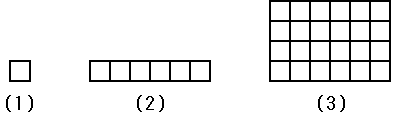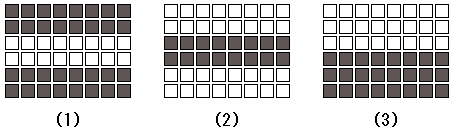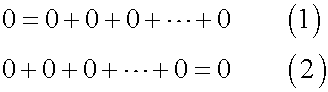- ユークリッド空間の数値化
- ビットマップ画像の限界
- ビットマップ画像からユークリッド幾何へ
- 点とは何か
ギリシャ人は無理数を発見して、さらに連速的なユークリッド空間を創り出しました。そこから発展したのが現代の数学です。現代数学は世界を連続的なものと見なしていて、数学の世界には自然数で表せない無理数が存在します。例えば円周率π、2の平方根√2などは自然数または自然数の比では表せません。数学ではそのままでもかまいませんが、現実に数学を適用しようとすると、どうしても近似値を用いなくてはいけませんので、有限の自然数のみを対象とする数学が必要になります。例えば建物や工業製品を作る場合には近似値を用います。特に今ではコンピューター制御の機械を用いるので、現実には近似値しか用いることが出来ません。これは人間の手で作業をしても同じです。人間が作業するには筋肉を用いるしかありません。筋肉の収縮は1本のα運動ニューロンが支配する筋繊維のまとまり、すなわち運動単位が最小の単位となっています。人間の筋肉の動きも分割不能な単位から構成されているのです。こう考えると、無理数は現実化出来無いということが分かります。つまり有限の自然数しか現実化出来無いのです。そしてそこには誤差が必ず存在します。
これは入力についても同様です。世界を認識するには光を用いるのが最も効率的ですが、網膜は視細胞で光を検出するので、必然的に目から得られる画像は画素から構成されています。細胞は分割不能なので、視細胞が分割不能な画素となります。二点を識別する能力を分解能と言いますが、人間の目の分解能は大体0.1mm程度です。デジタル機器を用いて精度を上げても、デジタル画像は画素から構成されているので、必ず解像度の限界があります。これは銀塩写真の場合も同じ事です。銀塩写真を人間の目で見れば、人間の目の解像度が限界になります。また銀塩写真のデータを数値化しようとすれば、写真を引き伸ばして定規で測らなくてはいけませんから、この場合も限界があります。一例としては、24X36mm(ライカ)判カメラで撮影した銀塩写真の解像度は、デジタルカメラの10メガピクセル程度と評価されています。こう考えると連続的なユークリッド空間は人間の脳内にしか存在しないことが分かります。図2にユークリッド空間とデジタル情報の関係を示しました。
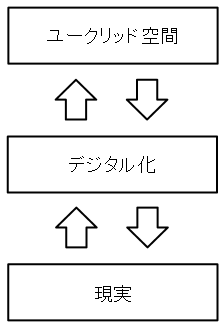
図1.ユークリッド空間の数値化
もしも世界そのものが連続的であっても、我々の世界の認識の仕方が離散的なので、世界をデジタルで認識するしか無いのです。図に示したように、ユークリッド空間での計算を現実に適用するには、どうしても数値化しなくてはならず、逆に現実をユークリッド空間でモデル化するにも数値化が必要です。つまり現実を自然数で表現する必要があるのです。
自然数を扱うのが数論であり、画像を扱うのが幾何学です。そして人間の認識の基本は自然数なので、数論から幾何学を構成することは、昔からの数学者の目標でした。しかし、それはなかなか上手くいかず、ユークリッドは公理に基づいて幾何学を構成しています。ヒルベルトも同様の試みをしています。私はこれらの試みは時期尚早だったと思います。人間がどうやって物を見るのか、人間が視覚的に外界を認識する過程が解明されるまでは、数論と幾何学をつなぐのは不可能だったと思われます。ヒルベルトやユークリッドが如何に優れていても、神経科学を知ることは出来なかったのです。ところが現代の神経科学の進歩は著しく、特に人間の視覚に関する研究は非常に進んでいます。現代においては平凡な頭脳の持ち主でも、神経科学を勉強しさえすれば、ユークリッド幾何と数論を結びつける方法を考えることが可能です。
コンピューターは自然数のみを扱い、にもかかわらず画像も扱えるので、コンピューターによる画像処理から話を始めます。一般的にコンピューターで使われているビットマップ画像では、画像を格子状の画素に分割し、各画素の色や明暗を数値で表します。この画素を単位正方形とすれば、平面を埋め尽くすことが可能です。しかも、単位正方形を自然数1に対応させれば、自然数1で図形を表すことが出来ます。図2-(1)に単位正方形を示します。単位正方形は自然数1に対応しているので、単位正方形の一辺の長さを1、面積を1と定義すれば便利です。この単位正方形は分割不能な画素となります。図2-(2)に長さ6の直線を示します。6個の単位正方形が一列に並んだ形になり、直線の幅は1となります。図2-(3)には高さ4、幅6の長方形を示します。長方形の面積は24となります。このようにして、単位正方形を用いて数論と幾何学をつなぐことが可能です。
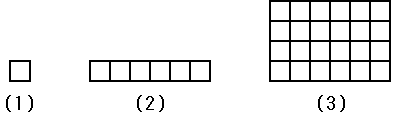
図2.単位正方形
このように自然数1を要素とする幾何学は構成されて、コンピューター幾何学と同様のものになります。これで実用上は十分のような気もします。ところが、古代ギリシャ人の開発したユークリッド幾何は、点の大きさは0、直線の幅も0となります。普通に考えると、線の幅が0では線は見えないし、点に大きさがなければ、点は存在しないのと同じと思われます。一見すると奇妙な幾何学が、数学の長い歴史の間、常に主流であったのです。その理由を考えるために、人間の視覚の考察から始めます。
生命が外界を認識するには光を用いるのが最も効率的です。そのための器官が眼ですが、眼はデジタルカメラと良く似た構造をしています。どちらもレンズと絞りがあり、光を検出するのは、デジタルカメラではCCD、眼では視細胞です。当然、眼球の網膜で最初に得られる画像はビットマップ画像です。二次元の画像についてはこれで十分のように思いますが、人間は三次元の世界を認識しなくてはいけません。
二次元と同じ原理を用いて三次元の世界を構成しようとすれば、ボクセルすなわち単位立方体が単位になります。実際のサイズに合わせて三次元の座標系を用いて、もしも正確な像が得られたならば、非常に生存競争には有利であると思われます。ただ遠方の物体の正確なサイズの推定は難しいと思われ、情報処理が複雑になります。さらに実用上の問題として、空間にも単位立方体が存在することになりますから、屋外の空間を表そうとした場合、あまりにも多くの単位立方体が必要となり、人間の脳の容量と処理能力を超えると思われます。
そこで生命の取った戦略は、三次元物体の形を認識するという方法です。そのために最も重要なのは、エッジの抽出で述べたように、一次視覚野の単純型細胞におけるエッジの抽出です。ヒューベルとウィーセルはこの発見によって1981年のノーベル生理学・医学賞を受賞しました。私はこの発見こそ、数学の基礎にとっても、神経科学にとっても革命的な大発見であると思います。彼らは、猫の後頭葉の一次視覚野の細胞を、刺激に対する反応から単純型細胞と複雑型細胞に分類しました。そのうちの単純型細胞を興奮させる最適刺激を図2に示します。
彼らは猫の一次視覚野の単純型細胞に電極を突っ込んで、その電位を記録しました。1個の単純型細胞は網膜の一定範囲の視細胞からの入力を受けて興奮します。彼らは色々な刺激を用いて、三種類の細胞を見出しました。図3-(1)は明るい線に反応する細胞、図3-(2)は暗い線に反応する細胞、図3-(3)は明暗の境界線に反応する細胞です。これらの細胞は特定の傾きの線分または明暗の境界線に反応します。
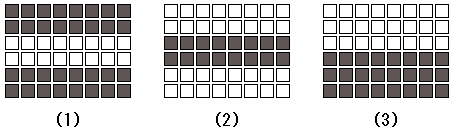
図3.単純細胞の最適刺激
ここでは、三番目の明暗の境界線に反応する細胞に注目します。この細胞の検出する境界線が物体のエッジになります。三次元の物体の形を認識する場合、重要なのはエッジの抽出であると述べました。具体的にエッジとは何かを考えます。まずは立方体について、立方体では各辺がエッジとなります。図4には真上から光が当たっている場合の影を示しました。正方形ABCDが立方体の影になり、線分AB、線分BC、線分CD、線分DAはそれぞれ明暗の境界線となります。このような明暗の境界線が物体のエッジに対応します。この境界線を我々の視覚は幅0の直線と認識します。この直線こそが、ユークリッドの定義する直線に対応します。つまり、一次視覚野の単純型細胞はユークリッドの定義する直線を検出するのです。ところが図3-(3)で明らかなように、ユークリッド直線は、ビットマップ画像の画素と画素の間を意味します。画素は自然数1に対応するので、ユークリッド直線は実体が無いことになります。平面幾何の範囲では、実体と考えられるのは面積だけです。面積はビットマップ画像における画素に対応します。ユークリッド幾何の構成は後に議論するとして、ここでは線に実体が無いということを確認して、視覚情報処理について先に話を進めます。
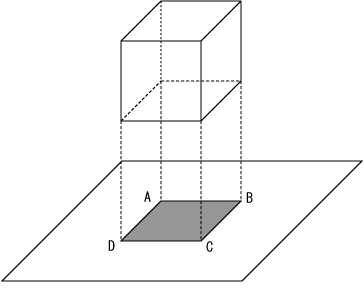
図4.立方体のエッジ
図5に球体のエッジを示します。球体の場合、光の方向と直交する大円がエッジとなります。エッジは一番出っ張った部分なので境界線となり、光の当たっている側は明るく、反対側は暗くなります。つまりエッジというのは、物体の出っ張った部分なので、網膜の二次元ビットマップ画像では明暗の境界線となり、視覚情報処理の最終段階には三次元物体の輪郭となります。
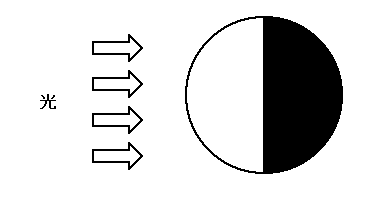
図5.球体のエッジ
ここで重要なことは、一次視覚野は三次元物体のエッジの検出に特化しているということです。つまり物体の形が認識されます。その時点で空間は空白として扱われ、人間は空間を実体として捉えません。三次元物体のエッジを検出して、物体の形を認識することが視覚認知の中心です。この時点で画素の存在は隠されるので、人間の目には空間は連続的なものと認識されます。物体までの距離は物体の相対的な位置関係や物体の大きさで推定されます。
図6に二つの立方体を示しています。図6を見た場合、近くの立方体と遠くの立方体と思うのが普通です。ただ2つの立方体の大きさについては、三通りの可能性があります。前の立方体と後ろの立方体が同じ大きさの場合、前の立方体が大きい場合、逆に後ろの立方体が大きい場合も考えられます。つまり、2つの立方体の大きさが分からない限り、両者の距離は分かりません。
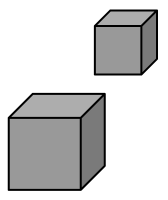
図6.物体の大きさ
図6の例では他に手がかりがないので、元の立方体の大きさがわからないと両者の距離は推定できません。それでも二つの立方体の大きさが分かっていれば、両者の距離を推定できます。それには空間の連続性が前提となります。このようにして、三次元の空間を認識する過程で、ユークリッド幾何を構成する上で基本的な2つの概念が発生します。空間の連続性と幅0の線です。この2つの概念に基づいてユークリッド幾何は構成されます。
前のセクションで、人間の脳の視覚情報処理の第一段階に関して解説しました。網膜の段階では画素は自然数1に対応するので、数論と幾何学の対応は明確です。ところが一次視覚野では画素に直接対応する神経細胞はありません。一次視覚野の中心的役割は三次元物体のエッジの検出です。それでも網膜の神経細胞の相対的位置関係は維持されます。網膜の相対的位置関係が維持されることをレチノトピーと呼びますが、レチノトピーのおかげで、物体の相対的な位置関係は維持されます。その時点で画素の存在は隠されますので、空間は連続的な物と認識されます。すなわち、数論とユークリッド幾何の関係は明示的ではなくなります。
空間の連続性を前提にユークリッド幾何を構成します。最も基本的な概念は、幅の無い直線になります。以下にユークリッド原論(Elements)の定義を6番目まで記載します。
第1巻 定義
- 点とは部分を持たないものである。
- 線とは幅のない長さである。
- 線の端は点である。
- 直線とはその上にある点について一様に横たわる線である。
- 面とは長さと幅のみをもつものである。
- 面の端は線である。
最初に5番の定義「面とは長さと幅のみをもつものである」をビットマップ画像との関係で考えると、面とは画素から構成されます。特にビットマップ画像では画素は単位正方形を表し、単位正方形は幅1長さ1です。また6番の定義「面の端は線である」によると、単位正方形の辺はユークリッドの定義する線に一致します。
次に幅0のユークリッドの定義する線を、三次元物体のエッジとの関係で考えてみます。二次元ビットマップ画像では、三次元物体のエッジは画素と画素の境界線となります。図7に白い画素と黒い画素の境界線として幅0の線分を赤で示しました。この場合は、線分は幅0でも画素と画素の境界線として認識できます。
続けてこの線分を中点で分割することを考えます。まず線分の端点は簡単に検出できます。ところが分割前には幅0の線分の中点は、幅も長さもないので簡単には検出できません。それでも両方の端点から等しい距離にある点で幅0の線分を分割した場合、図7に示したように線の端として2つの点が生じます。点は幅が0であるので、0=0+0、つまり点は2つに分割しても問題無いのです。中点で線分を切断すれば2つの点が実体化するのですから、最初の時点でも中点は潜在的に存在していたと考えるべきでしょう。
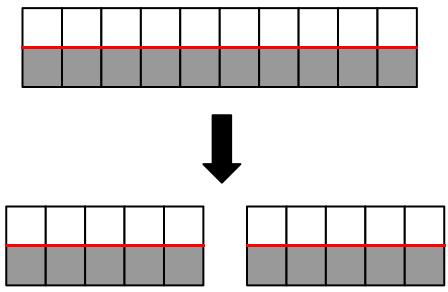
図7.幅0の線分の分割
このように点には実体が無いので、いくらでも分割可能です。以下の数式(1)で明らかです。ここまで来ると、何故ユークリッドが点とは部分を持たないと定義したのかが分かります。本来のギリシャ哲学の考え方からすると、点は分割不能であるとしたかったはずです。ところがそう出来無かったのです。また点には幅も長さも無いので、必然的に点をいくら集めても長さは生じません。数式(2)に示しています。
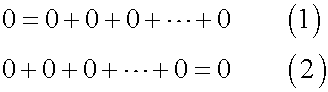
ここからはユークリッド図形を扱います。点の分割を図形化したのが図8です。図8のように円を8等分すると、8個の扇形になります。円の中心点は、扇形の8個の中心点に分割されます。図8で明らかなように、1個の点はいくらでも分割可能です。同様に線も分割可能で、図8では8本の線がそれぞれ二分割され16本の線が生じます。図8で明らかなように点には実体が無いので、いくらでも分割可能なのです。逆に点をいくら集めても長さは0です。
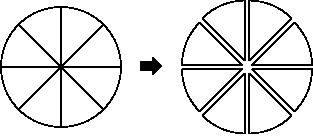
図8.点の分割
上の図8で1本の半径に注目します。半径の一方の端点は中心でもう一方の端点は円周上の点となります。当然、半径の2つの端点は一対一に対応します。つまり、つまり円周上の点をいくら集めても長さ0にしかならないのです。図8でも明確なように、点とは空白であるからなのです。ここから言えることは点から線を構成することは出来無いということです。
同様のことを線分について示したのが図9です。三角形OABがあるとします。線分ABと平行に三角形OAB内に直線CDを引きます。当然、線分ABよりも線分CDは短くなります。ところが線分AB上にある点の数は線分CD上にある点と等しくなります。ここで線分AB上の任意の点Pに三角形の頂点Oから直線OPを引きます。線分OPは線分CDと一点Qで交わります。ここで線分OQPに注目すると、点Oと点Qと点Pは一対一対一に対応します。最初にPとQは一対一に対応しますので、線分CD上の点の数と線分AB上の点の数は等しいのです。次に点Oは線分OCAの端点でもあるし、線分OPQの端点でもあるので、点Oは2点に分割可能です。同様の分割は何回でも可能です。すなわち点Oを分割して生じる点の数と、線分CD上の点の数と線分AB上の点の数は等しいのです。そして線分AB上および線分CD上の全ての点を合わせた長さと一点Oの長さは等しく、どちらもゼロです。
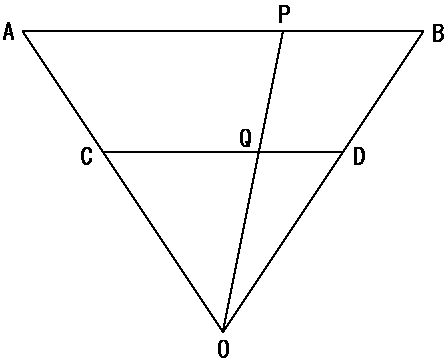
図9.線分上の点
点から長さを構成できないことを、別の方法で示したのが下の図10です。1本の線分を2等分し、さらに分割された線分を2等分します。これを何回繰り返しても線分の合計の長さは一定です。
図10.線の分割
注意すべき点として、上の図では分割をいくらでも繰り返せますが、その回数は自然数なので無限回繰り返すことは出来ません。また線分上には潜在的に無数の点が存在しますが、その個数を数えることは出来ません。何故ならば任意の長さの線分は、切断によっていくらでも点を生じる可能性があります。つまり点は線分の端として実体化した場合しか数えることは出来ません。さらに1個の点は、任意の本数の線分の端点となり得るからです。つまり1点は任意の個数の点に分割可能なのです。
ここまでの結論としては、点から線は構成できない。同様に線から面も構成できません。ユークリッドはこの事実を十分に認識していました。恐らくユークリッドは点から出発して、構成的に幾何学を構築したかったに違いありません。これは原論の冒頭の第1巻1番目に点を定義しようとしたことで明らかです。誰でも点が最も基本的な概念と思います。ところが3番目の定義で点を線の端として定義せざるを得ない羽目に陥ります。さらに6番目の定義で「面の端は線である。」と定義します。ユークリッドは不本意だったとは思いますが、この定義の順番は逆のように見えて必然性があります。これまで述べたように、ユークリッド平面はビットマップ画像から画素を隠して得られたものだからです。面は画素に対応するので、面から定義していくのが必然となります。