������
![]() ���O�̂Ƃ��A�@���̐�
���O�̂Ƃ��A�@���̐�![]() �̕�������
�̕�������![]() �A�|
�A�|![]() �̂ӂ�����
�̂ӂ�����
�ʂ̌�����������ƁA���鐔���Q�悵���@![]() �@(
�@(![]() ���O)�@�ƂȂ����̐���
���O)�@�ƂȂ����̐���![]() �ƕ\���B����
�ƕ\���B����![]() ���������Ƃ����B
���������Ƃ����B
�`���O�̂Ƃ��A���̐�(�|5)�Ȃǂ̕������͏�����![]() �̂ӂ�������
�̂ӂ�������
![]() �@�@ �Q�l�F
�@�@ �Q�l�F![]()
![]()
���Ȃ݂�![]() ��0�ł���
��0�ł���
����{������
�`���O�̂Ƃ��@�@![]() ���`�@�@�A�@�@
���`�@�@�A�@�@![]() ���`�@�A�@
���`�@�A�@![]() ��0
��0
![]() ���@ �` �@(�`��0�̂Ƃ�)
���@ �` �@(�`��0�̂Ƃ�)
�@ �|�` �@(�`��0�̂Ƃ�)
�܂��́A�@![]() ���b�`�b�@�Ƃ��Ă��悢
���b�`�b�@�Ƃ��Ă��悢
�@ ��![]() �̂Ƃ��ɕK�����̎����g���I��ł��̂킯��������܂��B
�̂Ƃ��ɕK�����̎����g���I��ł��̂킯��������܂��B
![]()
![]()
![]()
![]()
�o���@�@�@�@�@
![]() ��1.41421356
�q�g���q�g���j�q�g�~�S��
��1.41421356
�q�g���q�g���j�q�g�~�S��
![]() �� 1.7320508 �q�g�i�~�j�I�S����
�� 1.7320508 �q�g�i�~�j�I�S����
![]() �@���@2.2360679 �t�W�T�����N�I�[���i�N
�@���@2.2360679 �t�W�T�����N�I�[���i�N
![]() ���@ 2.6457513 �i�j���V�C�i�C
���@ 2.6457513 �i�j���V�C�i�C
![]() �@����́A
�@����́A![]() �����Ă͂܂�
�����Ă͂܂�
![]() �ɂ��� �@
�ɂ��� �@
![]() �̂悤�ȁ�̊O����2��ł͂Ȃ��A��̒���2��̌`�̏ꍇ�̂�肩���ł��B
�̂悤�ȁ�̊O����2��ł͂Ȃ��A��̒���2��̌`�̏ꍇ�̂�肩���ł��B
![]() �Ƃ́A
�Ƃ́A![]() ��
��![]() �@�܂�A(�|)�~(�|)=(�{)������
�@�܂�A(�|)�~(�|)=(�{)������![]() �̒��̕��̕����͏�����B
�̒��̕��̕����͏�����B
����āA ![]() �@�ɂ����������B�@�@
�@�ɂ����������B�@�@
�Ƃ���ŁA��̒��������̂Ƃ��B�܂�![]() �̂悤�������ł͂Ȃ��A
�̂悤�������ł͂Ȃ��A![]() ��
��![]() �悤�������̂Ƃ��ɁA
�悤�������̂Ƃ��ɁA![]() ���|3�Ȃǂ̂悤�����ł��邩������Ȃ��B�����̕������Ȃ�����ƁA��������
���|3�Ȃǂ̂悤�����ł��邩������Ȃ��B�����̕������Ȃ�����ƁA��������![]() ��
��![]() �Ƃ����玩���ł���B
�Ƃ����玩���ł���B
���̊Ԉ��������2�悵�Ă���ɂ�������炸�A![]() ���|3�ƕ����͂����o���Ă��܂��B
���|3�ƕ����͂����o���Ă��܂��B![]() �̒l�͕��ł��邩������Ȃ����Ƃɒ��ӂ��āB�����̂Ƃ��A��Βl���g�p���邱�Ƃɂ��A���̂悤�Ȃ�������~�X��h�~�ł���B��Βl�͕����̑���ŕK�����̐����͂����Ԃ��B��Βl|�|�R|���|(�|�R)���R�̂悤�Ɂ|1���|���Đ��ɂ���B����2�悷��ƕK�����ɂȂ�̂ł���́A��Βl�ƒʂ����B���L�̎��ł́�̒��������ł������ł��g����B
�̒l�͕��ł��邩������Ȃ����Ƃɒ��ӂ��āB�����̂Ƃ��A��Βl���g�p���邱�Ƃɂ��A���̂悤�Ȃ�������~�X��h�~�ł���B��Βl�͕����̑���ŕK�����̐����͂����Ԃ��B��Βl|�|�R|���|(�|�R)���R�̂悤�Ɂ|1���|���Đ��ɂ���B����2�悷��ƕK�����ɂȂ�̂ł���́A��Βl�ƒʂ����B���L�̎��ł́�̒��������ł������ł��g����B
![]() �@(
�@(![]() ��0) �@
��0) �@
![]() �@(
�@(![]() ��0) �@�@(���ށ�)b
��0) �@�@(���ށ�)b
���![]() �͕���������Ȃ��B���������Đ����̏ꍇ����������B
�͕���������Ȃ��B���������Đ����̏ꍇ����������B
![]() ��
��![]() �i�����̐��j�@�i
�i�����̐��j�@�i![]() ��0�̂Ƃ��j
��0�̂Ƃ��j
![]() �i�����̐��j�@�i
�i�����̐��j�@�i![]() ��0�̂Ƃ��j
��0�̂Ƃ��j
���(![]() >0), (
>0), (![]() <0)�̂����A�����̐������킩���Ă��邩��A�ꍇ�������Ȃ��Ă悢�ˁB
<0)�̂����A�����̐������킩���Ă��邩��A�ꍇ�������Ȃ��Ă悢�ˁB
![]() �@�Ƃ��Ă��ԈႢ���ˁB(�L-��-`)
�@�Ƃ��Ă��ԈႢ���ˁB(�L-��-`)
![]() �@(
�@(![]() >0), (
>0), (![]() <0)
<0)
����@(1)![]() �@�@(2)
�@�@(2)![]() �@�@(3)
�@�@(3)![]()
(4)![]() (5)
(5)![]() (6)
(6)![]()
(7) ![]()
![]() �̐������킩��Ȃ��̂ŏꍇ��������
�̐������킩��Ȃ��̂ŏꍇ��������
![]() ��0�̂Ƃ��||
��0�̂Ƃ��||![]() |���|1�E�|
|���|1�E�|![]() ��
��![]()
![]() ��0�̂Ƃ��||
��0�̂Ƃ��||![]() |���|1�E
|���|1�E![]() ���|
���|![]()
(8)![]() �@�@
�@�@
���̖��ł��̎����g���Ă邩��A�ꍇ�����̎d���͉����Q�l�ɂ���
(9)![]() �����@
�����@
�A�F![]() ��2�̂Ƃ��@|
��2�̂Ƃ��@|![]() |��
|��![]() �@�A|
�@�A|![]() �|�Q|��
�|�Q|��![]() �|�Q
�|�Q
����ć@��![]() (
(![]() �|�Q�{1)��
�|�Q�{1)��![]()
�C�F0��![]() ��2�̂Ƃ��@|
��2�̂Ƃ��@|![]() |��
|��![]() �@�A|
�@�A|![]() �|�Q|���|(
�|�Q|���|(![]() �|�Q)���|
�|�Q)���|![]() +�Q
+�Q
����ć@![]() (�|
(�|![]() �{�Q�{1)���|
�{�Q�{1)���|![]()
�E�F![]() ��0�̂Ƃ��@|
��0�̂Ƃ��@|![]() |���|
|���|![]() �@�A|
�@�A|![]() �|�Q|���|(
�|�Q|���|(![]() �|�Q)���|
�|�Q)���|![]() +�Q
+�Q
����ć@�́@�|![]() (�|
(�|![]() �{�Q�{1)��
�{�Q�{1)��![]()
�@�@�@�@�@���F![]() ��2�̂Ƃ��@
��2�̂Ƃ��@![]()
0��![]() ��2�̂Ƃ��@�|
��2�̂Ƃ��@�|![]()
![]() ��0�̂Ƃ��@
��0�̂Ƃ��@![]()
������̗L������ ����̕������͗L�������܂��傤
![]()
![]() �@�Ƃ��@
�@�Ƃ��@![]() ���Y��Ȃ��ŁB
���Y��Ȃ��ŁB
��P�@![]()
��Q�@
��3�@�@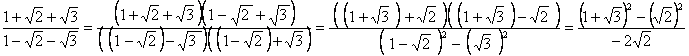
�@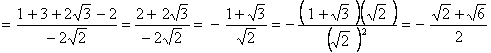
�ȉ��̗��2�͉������ɒ��ӂ��K�v���Ǝv���̂ōڂ��Ă݂��B
��4�@�@ �@�@
�@�@![]() �Ƃ����B
�Ƃ����B![]() ������A
������A
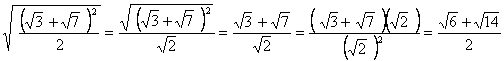
��5�@�@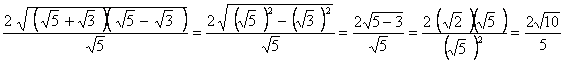
��2�d������
����0�A����0�̂Ƃ�
![]() �@
�@
�@
�⑫�F![]() �@(
�@(![]() ��0)�Ȃ̂ŁA
��0)�Ȃ̂ŁA![]() ��
��![]() �����炾��@
�����炾��@
�⑫�F![]() �@�Ȃ̂͂킩���ˁH
�@�Ȃ̂͂킩���ˁH
��1![]()
��Q![]()
��R ![]()
POINT�F![]() �Ƃ��Ȃ��悤�ɁI
�Ƃ��Ȃ��悤�ɁI ![]() ���A
���A
![]() ����āA
����āA![]() �̌`�ɂ���B
�̌`�ɂ���B
��4�@![]()
��T�@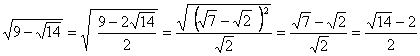 �@�Y�ꂸ�L�������܂��傤�B
�@�Y�ꂸ�L�������܂��傤�B
�����@�ˬ�`
���w�ڎ��ց�