＜関数とは？＞

２つの変数ｘ、yがあって�Iの値を定めると、それに対してyの値がただ１つ定まるとき、yはｘの関数であるという。

---

＜関数記号＞

●一般にyがｘの関数であることを　y＝f(ｘ)　のようにあらわす。ｆはFunction(関数)。

●関数の内容に応じて、式をｇ(ｘ)、ｈ(ｘ)などの文字で使い分けて表してよい。

●関数　y＝f(ｘ)について、ｘ＝ａのときのyの値はｆ(ａ)で表す。

　　例：�I＝２のとき　　y＝f(２)＝１０ｘ＋２＝２２

[関数の値]

　＊ｆ(ｘ)＝２ｘ²＋３ｘ−２、ｇ(ｘ、ｙ)＝ｘ²−ｘｙ＋３ｙのとき、次の値を求めよ。

　　　ｇ(３、１)＝３²−３・１＋３・１＝9　答

　　　ｆ(ｘ−1)＝２(ｘ−１) ²＋３(ｘ−１)−２＝２ｘ²−ｘ−３　答

---

＜関数のグラフ＞

関数y＝ｆ(ｘ)が与えられると　ｘの値を定めるごとに　yの値が定まる。　座標平面上で、この対応によって定まるｘとｙの値の組(ｘ、ｙ)、すなわち点(ｘ、ｆ(ｘ))を座標とする点全体の集合(図形)を関数ｙ=f(ｘ)のグラフという。したがって、点(ａ、ｂ)が関数ｙ＝ｆ(ｘ)のグラフ上にあることは、関係ｂ＝ｆ(ａ)が成りたつ。　ｙ＝ｆ(ｘ)の�Iの値に１、２、３、４、････で代入して�Iの値をどんどん変化させると、yの値もそれに対応して変化する。その変化をグラフに表したものが関数のグラフである。

---

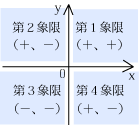
＜座標平面＞

座標軸ｘ、ｙの定められた平面を座標平面という。座標平面上の点Ｐの位置は2つの数の組(ａ、ｂ)で表される。この組(ａ、ｂ)を点Ｐの座標という。座標平面は座標軸で分けられた4つの部分をそれぞれ第1象限、第２象限、第３象限、第４象限という。

注意：座標軸上の点はどの象限にも含まれないです。

---

＜定義域・値域＞

関数ｙ＝ｆ(ｘ)において、�Iの変域をとくに指定して考える必要がある場合、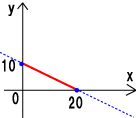
変数�Iの変域をこの関数の定義域という。

また、ｘが定義域内のすべての値をとるとき、
ｆ(ｘ)がとりうる値の範囲を　この関数の値域という。

つまり、ｘの変域が定義域、ｙの変域が値域。
図はｙ＝−0.5ｘ＋10の例で、変域が0≦ｘ≦20　のとき、値域は0≦ｙ≦10です。

---

＜最小値・最大値＞

関数の値域に最大の値があるとき、これをこの関数の最大値という。また
値域に最小値があるとき、これをこの関数の最小値という。
上の関数では、値域が0≦�I≦20なのでｘ＝0で最小値、ｘ＝20で最大値をとる。

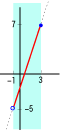
　例：ｙ＝３ｘ²−2　(−１＜ｘ≦３)の最大値、最小値があればそれを求めよ。

　　　ｙ＝３・(−１)−２＝−５、　　ｙ＝３・３−２＝７

　　　その値域は−５＜ｙ≦７　　よって、ｘ＝３で最大値7をとる。

　　　　＊ｘは−１を含まないので、最小値はない。　

---

＜１次関数のグラフ＞

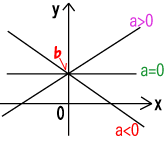
ｙ＝aｘ＋ｂのグラフ：　
　　　　ａは傾き、ｂはｙ切片(ｙ軸上の切片)、
　　　　a＞0のときは右上がり、a＜0のときは右下がり。

関数ｙ＝ｂのグラフ：　
　　　　傾きが0、ｙ切片がｂ、ｙ軸に垂直な直線である。
　　　　なお、関数ｙ＝ｂは１次関数ではない。定数関数という。

---

＜2次関数のグラフ＞

＊2つの変数ｘ、ｙがあって、ｙがｘの2次式で表される関数を　ｘの2次関数という。

2次関数の一般形：

　　　　　ｙ＝ａｘ²＋ｂｘ＋ｃ　ａ、ｂ、ｃは定数　ａ≠0

　　・下記の式は2次関数である。

　　　　　　　ｙ＝２ｘ^２、ｙ＝−５ｘ^２−1、ｙ＝３ｘ^２＋２ｘ＋１

---

＜ｙ＝ａｘ^２のグラフ＞

＊ｙ＝ａｘ^２のグラフは原点を通り、ｙ軸について対称な放物線。

ｙ＝ｘ^２　、ｙ＝−ｘ^２、ｙ＝２ｘ^２、ｙ＝−２ｘ^２、ｙ＝ｘ^２、ｙ＝−ｘ^２のグラフをみてみよう。

●このグラフのような左右対称な形の曲線を放物線という。

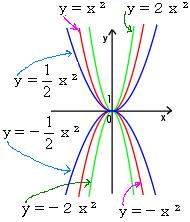
●曲線が対称の軸と放物線の交点をその放物線の頂点という。

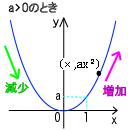
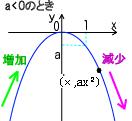
●ａ＞0のとき　下に凸、　ａ＜0のとき　上に凸である。

次にｙ＝ａｘ²のａについて説明しよう。上の式でいうと　２、−１、２、−２、、−などがａにあたるね。

●ａの絶対値が大きくなると、グラフの開き方は小さくなる (ｙ軸に近づく) 。

●ａはグラフの形を制御する(放物線の開き具合とか、上に凸とか)ものです。

●ａ＞0のとき　下に凸、　ａ＜0のとき　上に凸である。

ｙ＝ａｘ²のグラフ：　

　　軸はｙ軸、頂点は原点　　ａ＞0のとき下に凸、ａ＜0のとき上に凸

　 　  　　       　　　

---

＜ｙ＝ａｘ^２＋ｑのグラフ＞

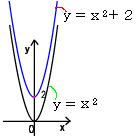
＊ｙ＝ａｘ²をｙ軸方向にｑだけ平行移動したものである。

　　軸はｙ軸、　頂点の座標は(0、ｑ)である。

　　　　例：ｙ＝ｘ²＋２　のグラフで、頂点の位置を確認して。→

---

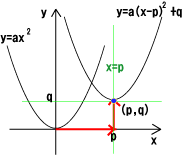
＜ｙ＝ａ(ｘ−ｐ) ²＋ｑ　のグラフ＞

＊ｙ＝ａｘ²をｘ軸方向にｐ、ｙ軸方向にｑだけ平行移動したものである。

　　軸の方程式は　�I＝ｐ、頂点の座標は　

●つまり、点(ｐ、ｑ)を原点とみてｙ＝ａｘ²のグラフをかけばよい。

---

＜ｙ＝ａｘ^２＋ｂｘ＋ｃのグラフ＞

＊ｙ＝ａｘ²を平行移動したものである。

●一般に2次式ａｘ^２＋ｂｘ＋ｃをａ(ｘ−ｐ) ²＋ｑの形に変形することを平方完成するという。言い換えると2次式を　完全平方＋定数　の形に変形することを平方完成するという。

ポイント：　2次式ａｘ^２＋ｂｘ＋ｃは　基本形ａ(ｘ−ｐ) ²＋ｑに直そう。　　

参考：一般の2次関数ｙ＝ａｘ²＋ｂｘ＋ｃは次の手順でｙ＝ａ(ｘ−ｐ) ²＋ｑの形に平方完成することができる。

　　　

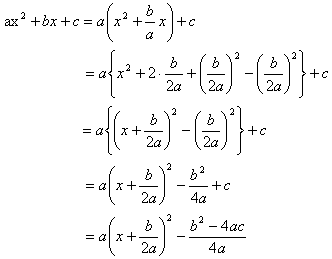
　　　　頂点は点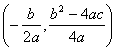　　　　軸は直線ｘ＝　

　　　　＊必ずｙ軸と点(0、ｃ)で交わる。

例：ｙ＝−３ｘ^２＋９ｘ−５のグラフの頂点の座標と軸の方程式を求め、グラフを書け。

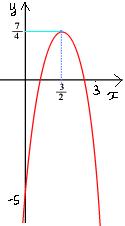　　ｙ＝−３ｘ^２＋９ｘ−５

　　　＝−３(ｘ^２−３ｘ)−５

　　

　　

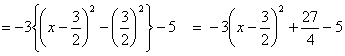
　　よって　頂点の座標は　、軸の方程式はｘ＝

2次関数ｙ＝ａｘ²＋ｂｘ＋ｃのグラフについて

　　ｘ＝0とおくと、ｙ＝−５となる。→グラフはｙ軸と必ず交わる。交点は点(0、−5)。

　　ｙ＝0とおくとａｘ²＋ｂｘ＋ｃ＝0　→この方程式が実数解をもてばそれがｘ軸との共有点のｘ座標になる。

　グラフは対称なので、ｙ＝−５となるのは、−より＝３　下の解説参照

　　　　　　　　　　　ｘ＝３、0のとき　ｙ＝−5である。

---

＜平方完成＞

とても重要です。方程式を平方完成すると、頂点の座標がわかります。

ｙ＝ａ(ｘ−ｐ) ²＋ｑ

　　　　　　　　　　すると、頂点は(ｐ、ｑ)である。

例：ｙ＝3(ｘ−５) ²＋２　の頂点の座標は？　←　上の平方完成の式と同じ形ですね。

　　●(　) ²の(　)の中を0にするｘを求めればよい。ｘ−５＝0　　→　ｘ＝５

　　●ｑにあたる部分はここの数字がそのまま頂点のｙ座標である。→　ｙ＝2

　　　　よって、頂点の座標は(５，２)　となります。

---

＜ｙ＝ａ(ｘ−α)(ｘ−β)のグラフ＞

ｙ＝ａ(ｘ−α)(ｘ−β) (α≠β)のグラフは、ｘ軸と交わる点が(α、0)(β、0)である。　これからグラフの対称性により、軸の方程式が求められる。軸は　ｘ＝　です。(補足参照)　軸の部分が頂点になるから、ｘ＝の値を与式に代入する。それにより、頂点の座標がわかる。

補足：ｘ＝２、８であるとき、その範囲のど真ん中が軸になる。よって、ｘ＝ とすると、丁度ｘの交点間のド真ん中の値（軸）が求められる。

　解説　：ａｘ^２＋ｂｘ＋ｃの平方完成によりａｘ^２＋ｂｘ＋ｃ＝より、�I軸は−である。

「解と係数の関係」より、2次方程式ａｘ²＋ｂｘ＋ｃの2つの解をα、βとすると

α＋β＝である。なぜそうなのか？

ａｘ²＋ｂｘ＋ｃ＝ａ(ｘ−α)(ｘ−β)＝ａｘ²−ａ(α＋β)ｘ＋ａαβ

これにより、ｂ＝−ａ(α＋β)、ｃ＝ａαβである。

ｂ＝−ａ(α＋β)　→　−ａを移行→　α＋β＝　←　なぜ同値か？　

それのｂを−ａ(α＋β)で代入すると　→　α＋β＝　ほら、同値である。

●以下の方法は係数が複雑で平方完成が難しい場合に特に有効である。

ｙ＝ａｘ²＋ｂｘ＋ｃ＝ａｘ(ｘ＋)＋ｃより、ｙ＝ｃとなるのはｘ＝0、−である。

具体例でいうと、ｙ＝２ｘ^２−４ｘ＋３で、ｙ＝３となるのは、２ｘ^２−４ｘ＝３　より

２ｘ(ｘ−２)＝３で、　ｘ＝０、２（つまり−）のときである。

●グラフの軸の方程式ｘ＝　は、�I軸の交点間０〜−のど真ん中が軸であるので、−を２で割ればよいので、軸の方程式はｘ＝−となる。

　　したがって、ｘ＝−＝−　　となる。　You got it?

例：ｙ＝２ｘ^２−４ｘ＋３を平方完成する。

　　　　ｙ＝２ｘ^２−４ｘ＋３

　　　　　＝２(ｘ^２−２ｘ)＋３

　　　　　＝２｛(ｘ−１) ^２−１^２｝＋３

　　　　　＝２(ｘ−１) ^２−２＋３

　　　　　＝2(ｘ−１) ^２＋１

　別解）　ｙ−ｑ＝ｆ(ｘ−ｐ)　つまり、ｙ＝ｆ(ｘ−ｐ)＋ｑより、
　 　　　ｙ−２＝２(ｘ−３) ^２−４(ｘ−３)＋３→　ｙ＝２ｘ^２−１６ｘ＋３５

例：ｙ＝(ｘ＋２)(ｘ−4)のグラフの頂点の座標と軸の方程式をもとめて、グラフをかけ。

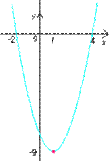　 ｙ＝0とおくと、ｘ＝−２、3　です。　グラフとｘ軸との交点は(−２、0)(4、0)です。

　　グラフの対称性により、軸の方程式は　ｘ＝だから、

　　ｘ＝　　ゆえに軸の方程式　ｘ＝1　

　　これを与式に代入して、ｙ＝(１＋２)(１−４)＝−９

　　

　　　したがって、頂点の座標は(１，−９)

---

＜グラフの平行移動＞ｙ＝ｆ(ｘ−ｐ)＋ｑ

ポイント�@：ｙ＝ａｘ^２＋ｂｘ＋ｃを平行移動してもａは変わらない!!

ポイント�A：以下の２つの方法がある。　　　　

　　　　　　●頂点の座標をもとめたやり方(平方完成)。

　　　　　　●ｙ＝ｆ(ｘ−ｐ)＋ｑ　の式を使うやり方。(下記参照)

　＊ｘ軸方向にｐ、ｙ軸方向にｑだけの平行移動によって

　方法�@点(ａ、ｂ)は点(ａ＋ｐ、ｂ＋ｑ)に移る。

　　方法�Aｙ＝ｆ(ｘ)のグラフは　ｙ＝ａ(ｘ−ｐ) ²＋ｑ　のグラフになる。

　 　　

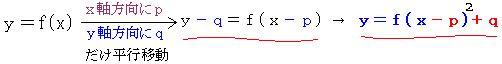
例：ｙ＝３ｘ^２−4ｘ＋3を�I軸方向へ、y軸方向へ−平行移動したときの放物線の方程式をもとめよう。

　　方法�@でのやりかたで解いてみよう。

　　与式を平方完成するとｙ＝３(ｘ−)^２−＝３(ｘ−)^２＋
　　→頂点の座標は(、)→　移動後の頂点の座標は(＋、−)→(1、1)
　　よって、ｙ＝3(ｘ−１) ^２＋１　方程式は→ｙ＝3ｘ^２−6ｘ＋4

　　　方法�Aのやりかたでやってみよう。　

　　ｙ−(−)＝３(ｘ−)^２−4(ｘ−)＋3　→ｙ＝3ｘ^２−6ｘ＋4

例：ｙ＝−ｘを(３，−２)だけ平行移動したものを求めよ。

　　ｙ−(−２)＝−(ｘ−３) ^２　　　　　∴ｙ＝−(ｘ−３) ^２−２

例：ｙ＝２ｘ^２−４ｘ＋３をｘ軸方向へ３、ｙ軸方向へ２、移動した場合。

　　ｙ＝２(ｘ−１) ^２＋１より頂点の座標を求め、

　　　(１，１)→(１＋３、１＋２)→(４，３)　よって、

　　　ｙ＝２(ｘ−４) ^２＋３→　ｙ＝２ｘ^２−１６ｘ＋３５

　
例:放物線ｙ＝３ｘ^２−６ｘ＋５をｘ軸方向にｓ、ｙ軸方向にｔだけ平行移動させると、放物線ｙ＝ａｘ^２＋１２ｘ＋１６となる。このとき、ａ、ｓ、ｔを求めよ。

　ｙ＝３ｘ^２−６ｘ＋５・・・・・�@

　ｙ＝３ｘ^２＋１２ｘ＋１６・・・・�A←「平行移動してもａは変わらない！」のでａ＝３

　�@より、ｙ＝３(ｘ−１) ^２＋２　よって、頂点は(１，２)

　�Aより、ｙ＝３(ｘ＋２) ^２＋４　よって、頂点は(−２、４)

　　ｘの移動量：−２−１＝−３　よって、ｘ軸方向に−３

ｙの移動量：４−２＝２　　　よって、ｙ軸方向に２

　　ａ＝３、ｓ＝−３、ｔ＝２　答

例：ｙ＝−ｘ^２＋４ｘ＋５についてｘ軸との交点の座標を求めよ。

　　−ｘ^２＋４ｘ＋５＝0　とおく。

　　ｘ^２−４ｘ−５＝0　→　(ｘ＋１)(ｘ−５)＝0　　よって(−1、0)、(５、0)答

例：ｙ＝２ｘ^２−４ｘ＋３を平行移動させたもので、2点(−2、−11)、(１、4)を通る。

　　　＊2次の係数２は平行移動しても変化しない。

　　　よって、ｙ＝２ｘ^２＋ｂｘ＋ｃに2点を代入してｂ、ｃを連立でもとめよう

　　　−11＝２・(−2) ^２＋(−１)ｂ＋ｃ　→　８−ｂ＋ｃ＝−11

　　　４＝２・１^２＋１・ｂ＋ｃ　→　２＋ｂ＋ｃ＝４

　　　　　　　　ｂ＝７、ｃ＝−５　　∴ｙ＝２ｘ^２＋７ｘ−５答

---

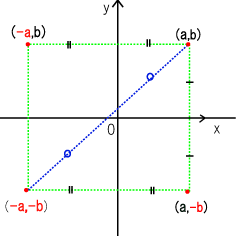
＜グラフの対称移動＞

点(ａ、ｂ)とすると

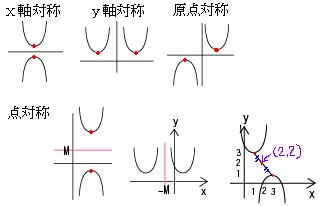
　�@ｘ軸に関して対称移動した放物線の方程式　　ｙ＝−ｆ(ｘ)　　→点(ａ、−ｂ)

　�Aｙ軸に関して対称移動した放物線の方程式　　ｙ＝ｆ(−ｘ)　　→点(−ａ、ｂ)

　�B原点に関して対称移動した放物線の方程式　　ｙ＝−ｆ(−ｘ)　→点(−ａ、−ｂ)

　　 　

	�I軸に対称	ｙ軸に対称	原点に対称
点(ａ、ｂ)	（ａ、−ｂ）	（−ａ、ｂ）	（−ａ、−ｂ）
グラフｙ＝ｆ(ｘ)	ｙ＝−ｆ(ｘ)	ｙ＝ｆ(−ｘ)	ｙ＝−ｆ(−ｘ)

例：ｙ＝ｘ^２−6ｘ＋11のグラフを(1)�I軸、(２)ｙ軸、(3)原点のそれぞれに関して対称移動した曲線をグラフにもつ2次関数を求めよ。

(1)    ｙ＝−ｆ(ｘ)より　ｙ＝−(ｘ^２−6ｘ＋11)　　　→　ｙ＝ｘ^２＋6ｘ−11

(2)    ｙ＝ｆ(−ｘ)より　ｙ＝(−ｘ)^２−6(−ｘ)＋11　→　ｙ＝ｘ^２＋6ｘ＋11

(3)    ｙ＝−ｆ(ｘ)より　ｙ＝−｛(−ｘ)^２−6(−ｘ)＋11｝→　ｙ＝−ｘ^２−6ｘ−11

また、下記のように考えてもよい。2次関数ｙ＝ａｘ^２＋ｂｘ＋ｃのグラフは、頂点の位置とｘ^２の係数ａで決まる。

基本形はｙ＝ａ(ｘ−ｐ) ^２＋ｑ　　頂点(ｐ、ｑ)で位置、そしてaで形が定まる。

(別解) 基本形に直す→ｙ＝(ｘ−3) ^２＋2　　これにより、頂点の座標は(3、2)

　　　�I軸の対称移動：　(3、2)→(3、−2)　　　　−ａ　⇒　ｙ＝−(ｘ−3) ^２−2

　　　ｙ軸の対称移動：　(3、2)→(−3、2)　　　　ａ　⇒　ｙ＝(ｘ＋3) ^２＋2

　　　原点の対称移動：　(3、2)→(−3、−2)　　−ａ　⇒　ｙ＝−(ｘ＋3) ^２−2

例：　放物線ｙ＝ｘ^２−2ｘ−3を�I軸に関して対称移動して得られる放物線の方程式は？

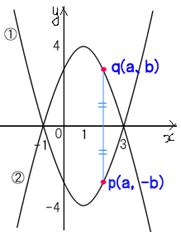
　　　グラフもかけ。

　　　ｙ＝ｘ^２−2ｘ−3・・・・�@

　　　ｙ＝(ｘ−１) ^２−４　←頂点の座標は(１、−４)

そして　ｙ＝(ｘ＋１)(ｘ−３)　←ｘ軸との交点は�I＝−１、３

　　　�@の対称移動は、ｙ＝−ｆ(ｘ)より、

　　　ｙ＝−ｘ^２＋２ｘ＋３・・・・�A



数学目次へ→