پƒ2ژںٹضگ”‚جچإ‘هپEچإڈ¬پ„
ٹضگ”‚ج’lˆو‚ةچإ‘ه‚ج’l‚ھ‚ ‚é‚ئ‚«پA‚±‚ê‚ً‚±‚جٹضگ”‚جچإ‘ه’l‚ئ‚¢‚¢پA’lˆو‚ةچإڈ¬’l‚ھ‚ ‚é‚ئ‚«پA‚±‚ê‚ً‚±‚جٹضگ”‚جچإڈ¬’l‚ئ‚¢‚¤پB
پ@
پ–’è‹`ˆو‚ب‚ا‚ةگ§Œہ‚ھ‚ ‚éڈêچ‡‚ًٹـ‚ك‚ؤپAچإ‘ه’lپEچإڈ¬’l‚ةٹض‚·‚é–â‘è‚إ‚حپ@پ@
پ@پ@پ@2ژںٹضگ”‚™پپ‚پ‚ک‚Qپ{‚‚‚کپ{‚ƒ(‚پپ‚0)‚جچإ‘ه’l‚ـ‚½‚حچإڈ¬’l‚ح
پ@پ@پ@پ@پ@ٹî–{Œ`پFپ@‚™پپ‚پ(‚کپ|‚گ) ‚Qپ{‚‘پ@‚جŒ`‚ة‚·‚邱‚ئپB
پ–چإ‘ه¥چإڈ¬‚ب‚ç‚Qژںٹضگ”‚ًٹî–{Œ`‚™پپ‚پ(‚کپ|‚گ) ‚Qپ{‚‘پ@‚جŒ`‚ة‚·‚éپB——R‚حپAچإ‘ه¥چإڈ¬‚حژ²‚جˆت’u‚ة‚و‚ء‚ؤŒˆ‚ـ‚é‚©‚ç‚إ‚·پB
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@
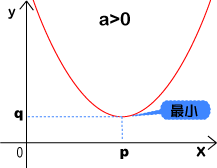
‚Qژںٹضگ”‚™پپ‚پ‚ک‚Qپ{‚‚‚کپ{‚ƒ‚جƒOƒ‰ƒt‚ح’è‹`ˆو‚ھژہگ”‘S‘ج‚ج‚ئ‚«
پ@پ@پ@پœ‚پپ„0‚ج‚ئ‚«پ@‚کپپ‚گ‚إچإڈ¬’l‚‘پ@(چإ‘ه’l‚ح‚ب‚¢)
پ@پ@پ@پœ‚پپƒ0‚ج‚ئ‚«پ@‚کپپ‚گ‚إچإ‘ه’l‚‘پ@(چإڈ¬’l‚ح‚ب‚¢)
‚إپA‚»‚ê‚حƒOƒ‰ƒt‚ج’¸“_‚ج‚™چہ•W‚إ‚ ‚éپBپ@‚آ‚ـ‚èپA
پ@‚کپپ‚گ‚ج‚ئ‚«پA‚»‚ê‚ج‚™چہ•W‚ھچإڈ¬’lپEچإ‘ه’l‚ً‚ئ‚éپB
پ@
 پ@پ@پ@پ@
پ@پ@پ@پ@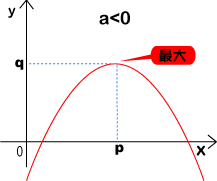
پƒ’è‹`ˆو‚ھگ§Œہ‚³‚ê‚ؤ‚¢‚éڈêچ‡پ„
’è‹`ˆو‚ةگ§Œہ‚ھ‚ ‚é‚ئ‚«‚حپA‚»‚جگ§Œہ‚ج‚ک‚ج”حˆح‚إ‚™‚ج’l‚ج•د‰»‚ً’²‚ׂؤپAچإ‘ه‚ـ‚½‚حچإڈ¬‚ً‹پ‚ك‚éپBپ@’è‹`ˆو(—خ‚ج‹éŒ`)“à‚ة‚ ‚é•ْ•¨گü‚جچإڈ¬پEچإ‘ه‚ً‚ف‚آ‚¯‚éپB
پ@پœچإ‘هپEچإڈ¬‚حژ²‚©‚牓‚—£‚ꂽ‚ک“_‚ھچإ‘ه(‚پپ„0)پA‚ـ‚½‚حچإڈ¬(‚پپƒ0)‚ئ‚ب‚éپB
پ@پœ2ژںژ®‚حٹî–{Œ`‚پ(‚کپ|‚گ) ‚Qپ{‚‘‚ة’¼‚µ‚ؤƒOƒ‰ƒt‚ً•`‚پB
پ@پœƒOƒ‰ƒt‚ج’¸“_‚جْIچہ•W(ژ²‚کپپ‚گ)‚ئ—¼’[‚ج‚™‚ج’l‚ً”نٹr‚µ‚ؤچإ‘هپEچإڈ¬‚ًŒˆ‚ك‚éپB
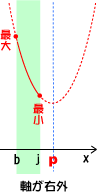
پ@پœژ²‚جˆت’u‚ة‚و‚è‰؛گ}‚جƒpƒ^پ[ƒ“‚إچإ‘ه¥چإڈ¬‚ھ•د‚ي‚éپB(‰؛گ}‚ح‚پپ„0‚ج‚ئ‚«)پ@
پ@پ@پ@‚پپƒ0‚جڈêچ‡پAƒOƒ‰ƒt‚ھڈم‚ة“ت‚إپAچإ‘هپEچإڈ¬‚ھ“ü‚ê‘ض‚ي‚éپB
پœ ژ²‚ھ‚‚پ…‚کپ…‚ٹ‚ج‚ا‚جˆت’u‚©‚ة’چ–عپB
پœ ‚پپ„0‚جڈêچ‡پA•ْ•¨گü‚جژ²‚ئ•دˆو‚ج’†گS‚جˆت’u‚ھˆê’v‚µ‚ؤ‚¢‚é‚ئ‚±‚ë‚ً‹«‚ة‚µ‚ؤپA‚»‚ج•ْ•¨گü‚جژ²ˆت’u‚ئ•دˆو(’è‹`ˆو)‚ج’†گS“_‚ئ‚جˆت’u‚ة‚و‚èپA‚»‚جژ²ˆت’u‚ئ‚ح”½‘خ‘¤‚ج•دˆو‚جچإ’[“_‚ھچإ‘ه‚ئ‚ب‚éپB—ل‚¦‚خپA‰؛گ}‚إ•دˆو(’è‹`ˆو)‚ج’†گS“_‚و‚èژ²‚ھ‰E‘¤‚ة‚ ‚ê‚خپA‚کپپ‚‚‚ج‚ئ‚«‚ج‚™چہ•W‚ھچإ‘ه’l‚ئ‚ب‚éپB‰؛گ}ژQچlپI
پ@پœ‚پپ„0‚ج‚ج‚ئ‚«‚ةچإڈ¬’l‚ً‹پ‚ك‚éڈêچ‡پAژ²‚ھ•دˆو“à‚ة‚ ‚ê‚خ‚کپپ‚گ(’¸“_)‚إچإڈ¬‚ئ‚ب‚èپA‹وٹشٹO‚ةژ²‚ھ‚ ‚é‚ئ‚«‚حژ²‚ة‹ك‚¢’[‚إچإڈ¬‚ئ‚ب‚éپB‰؛گ}ژQچlپI
 پ@پ@
پ@پ@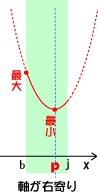 پ@
پ@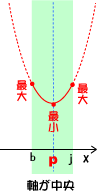 پ@
پ@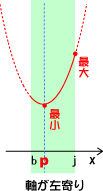 پ@
پ@ پ@
پ@
پ@پ@
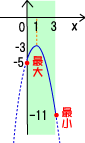
—لپFٹضگ”‚™پپپ|‚Q‚ک‚Qپ{‚S‚کپ|‚T(‚Oپ…‚کپ…3)چإ‘ه’l¥چإڈ¬’l‚ً‹پ‚ك‚وپB
پ@‚™پپپ|‚Q‚ک‚Qپ{‚S‚کپ|‚T‚ً•دŒ`‚µ‚ؤپA‚™پپپ|‚Q(‚کپ|1) ‚Qپ|3پ@’¸“_‚ح(1پAپ|3)
پ@پ@‚کپپ0‚ج‚ئ‚«پ@‚™پپپ|‚QپE0‚Qپ{‚SپE0پ|5پپپ|5پ@‚™پپپ|‚Tپ@(چ¶’[‚ج’l)
پ@پ@‚کپپ‚R‚ج‚ئ‚«پ@‚™پپپ|‚Q(‚Rپ|‚P) ‚Qپ|‚Rپپپ|11پ@‚™پپپ|11پ@پi‰E’[‚ج’lپj
پ@‚و‚ء‚ؤ‚کپپ0‚إچإ‘ه’lپ\‚TپA‚کپپ‚R‚إپ|11
پ@پ@پ@
پƒ‹وٹش‚جˆê’[‚ھ“®‚ڈêچ‡پ„
•دˆوپi’è‹`ˆوپj‚جˆê’[‚ھ•دگ”‚ئ‚ب‚èپA‚»‚ج•دگ”‚ج‘‰ء‚إ•دˆو‚ھچL‚ھ‚èپAچإ‘ه’lپEچإڈ¬’l‚ً”»’f‚·‚é‚ة‚حپAٹeڈêچ‡‚جƒOƒ‰ƒt‚ً•`‚«پA‹وٹش‚ج—¼’[‚ج’l‚ً”ن‚ׂéپBƒ|ƒCƒ“ƒg‚ح•ْ•¨گü‚جژ²‚ئ•دˆو‚ج’†گS‚جˆت’u‚ھˆê’v‚µ‚ؤ‚¢‚é‚ئ‚±‚ë()‚ً‹«‚ة‚µ‚ؤپA‚»‚ج•ْ•¨گü‚جژ²‚ئ•دˆو‚ج’†گS“_‚ئ‚جˆت’u‚ة‚و‚èپAچإ‘ه’lپEچإڈ¬’l‚ً”»•ت‚·‚éپB
—لپF0پ…‚کپ…‚پ‚ة‚¨‚¯‚éٹضگ”پ@‚™پپپ|2‚ک‚Qپ{4‚کپ{1‚جچإڈ¬’l‚ً‹پ‚ك‚وپB
پ@پ–ڈم‚ة“ت‚جƒOƒ‰ƒt‚ة‚ب‚é‚ج‚إ‚·پBژ²‚ئ’è‹`ˆو‚جچ¶’[‚ھŒإ’肵‚ؤ‚ـ‚·پBƒ|ƒCƒ“ƒg‚ح•دˆو(’è‹`ˆو)‚ج—¼’[‚إ“¯ژ‚ةچإڈ¬’l‚ًژو‚éڈêچ‡(•ْ•¨گü‚جژ²‚ھ’è‹`ˆو‚ج’†‰›‚ئˆê’v‚·‚é‚ئ‚«)پA‚آ‚ـ‚èf(0)پپ‚†(‚پ)‚ئ‚ب‚é‚پ‚ج’l‚إ‚·پB‚»‚ج’l‚ًٹîڈ€‚ة‚µ‚ؤچl‚¦‚ؤ‚¢‚±‚¤پB‚±‚جٹîڈ€‚ة‚ب‚é’l‚پ‚ح(•ْ•¨گü‚جژ²‚ھ’è‹`ˆو‚ج’†‰›“_‚ئˆê’v‚·‚é‚ئ‚«)پAژ²‚ج•û’ِژ®‚ج2”{‚ب‚ج‚إپA
پ@ٹضگ”‚ً•دŒ`‚µ‚ؤپA‚™پپپ|‚Q(‚کپ|‚P)پ{3پ@’¸“_‚ح(‚PپA3)پ@
ژ²‚ج•û’ِژ®‚ح‚کپپ‚Pپ@پ¨پ@‚پپپ‚Qپ@پ@پ©‚±‚ê‚ًٹîڈ€‚ةچl‚¦‚éپB
(•دˆو0پ…‚کپ…‚پ‚ج’†‰›’l‚کپپ![]() ‚ھژ²‚کپپ‚P‚ةˆê’v‚·‚é‚ج‚إ‚پپپ‚Q‚کپ@‚و‚ء‚ؤپA‚پپپ‚Q)پ@
‚ھژ²‚کپپ‚P‚ةˆê’v‚·‚é‚ج‚إ‚پپپ‚Q‚کپ@‚و‚ء‚ؤپA‚پپپ‚Q)پ@
‚±‚±‚©‚çپA‚پ‚ج’l‚إ‚جڈêچ‡•ھ‚¯‚ً‚µ‚ؤپAچإڈ¬’l‚ً‹پ‚ك‚ـ‚·پB
ƒAپF‚Oپƒ‚پپƒ2‚ج‚ئ‚«
پ@پ@پ@•دˆو‚جچ¶’[پA‚·‚ب‚ي‚؟‚کپپ0‚إچإڈ¬‚ئ‚ب‚èپA‚™‚ج’l‚ھچإڈ¬’lپB‚و‚ء‚ؤ‚P‚ً‚ئ‚é
پ@ƒCپF‚پپپ‚Q‚ج‚ئ‚«
پ@پ@پ@•دˆو‚ج—¼’[پA‚·‚ب‚ي‚؟پA‚کپپ0پA2‚إچإڈ¬‚ئ‚ب‚èپA‚™‚ج’l‚ھچإڈ¬’lپB‚و‚ء‚ؤ‚P‚ً‚ئ‚é
پ@ƒEپF‚Qپƒ‚پ‚ج‚ئ‚«
پ@پ@پ@•دˆو‚ج‰E’[پA‚·‚ب‚ي‚؟پA‚کپپ‚پ‚إچإڈ¬‚ئ‚ب‚èپAچإڈ¬’lپ|‚Q‚پ‚Qپ{‚S‚پپ{‚P‚ً‚ئ‚éپB
پ@ƒAپ`ƒE‚ً‚ـ‚ئ‚ك‚é‚ئپA0پ…‚کپ…‚پ‚ة‚¨‚¯‚éچإڈ¬’l‚ح
پ@پ@پ@0پƒ‚پپ…‚Q‚ج‚ئ‚«پ@پ@چإڈ¬’lپ@‚P
پ@پ@پ@‚Qپƒ‚پ‚ج‚ئ‚«پ@پ@چإڈ¬’lپ@پ|‚Q‚پ‚Qپ{‚S‚پپ{‚P
پ@پ@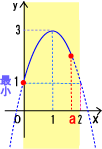 پ@پ@
پ@پ@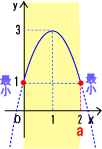 پ@پ@
پ@پ@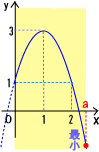
—لپF‚Oپ…‚کپ…1‚ة‚¨‚¯‚éٹضگ”‚™پپ‚ک‚Qپ|‚Q‚گ‚ک‚جچإڈ¬’l‚ً‹پ‚ك‚وپBپ@
پ@پ@‰؛‚ة“ت‚جƒOƒ‰ƒt‚إ‚·پBژ²‚ھ•دˆو“à‚ةٹـ‚ـ‚ê‚éڈêچ‡پA’¸“_‚ھچإڈ¬’lپB‚»‚¤‚إ‚ح‚ب‚¢ڈêچ‡پA—¼’[‚ج‚¢‚¸‚ê‚©‚ھچإڈ¬’l‚ئ‚ب‚éپB‚و‚ء‚ؤپAڈêچ‡•ھ‚¯‚·‚éپBپ@
ٹضگ”‚™پپ‚ک‚Qپ|‚Q‚گ‚ک‚ً•دŒ`‚µ‚ؤپA
‚™پپ(‚کپ|‚گ) ‚Qپ|‚گ‚Qپ@پ@پ@’¸“_‚ح“_(‚گپAپ|‚گ)پAپ@ژ²‚کپپ‚گ
‚±‚جژ²‚کپپ‚گ‚ھ‚Oپ…‚کپ…1‚ج•دˆو‚ةٹـ‚ـ‚ê‚é‚©”غ‚©‚إڈêچ‡•ھ‚¯‚·‚éپB
•â‘«پF‚ک‚Qپ|‚Q‚گ‚کپپ‚ک(‚کپ|‚Q‚گ)پ@‚و‚è‚کپپ0پA2‚گپ©‚کژ²‚جŒً“_
پ@پ@پ@‚کپپ‚P‚ج‚ئ‚«‚ک‚Qپ|‚Q‚گ‚کپپ‚P‚Qپ|‚Q‚گپE‚Pپپ‚Pپ|‚Q‚گپ©‚کپپ‚P‚ج‚ئ‚«‚ج‚™‚ج’l
ƒAپF‚گپƒ0‚ج‚ئ‚«پ@
پ@پ@پ@•دˆو‚جچ¶’[(‚کپپ0)‚إچإڈ¬‚ئ‚ب‚èپA‚™‚ج’l‚ھچإڈ¬’lپB‚و‚ء‚ؤ0‚ً‚ئ‚éپB
ƒCپF0پ…‚گپƒ‚P‚ج‚ئ‚«پ@پ@
پ@پ@پ@’¸“_‚ھ•دˆو“à‚ةٹـ‚ـ‚ê‚é‚ج‚إ‚کپپ‚گ(’¸“_)‚إچإڈ¬‚ئ‚ب‚éپB
پ@پ@پ@پ@‚™‚ج’l‚ھچإڈ¬’l‚ب‚ج‚إپAچإڈ¬’lپ|‚گ‚Q‚ً‚ئ‚éپB
پ@ƒEپF‚Pپ…‚گ‚ج‚ئ‚«پ@پ@
پ@پ@پ@پ@•دˆو‚ج‰E’[(‚کپپ‚P)‚إچإڈ¬‚ئ‚ب‚èپA‚™‚ج’l‚ھچإڈ¬’lپBچإڈ¬’l‚Pپ|‚Q‚گ‚ً‚ئ‚éپB
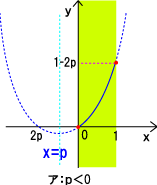
پ@‚ـ‚ئ‚ك‚é‚ئپA“ڑپF‚گپƒ0‚ج‚ئ‚«پ@چإڈ¬’l0
پ@پ@پ@پ@پ@پ@پ@پ@پ@0پ…‚گپƒ‚P‚ج‚ئ‚«پ@چإڈ¬’lپ|‚گ‚Q
پ@پ@پ@پ@پ@پ@پ@پ@پ@‚Pپ…‚گ‚ج‚ئ‚«پ@چإڈ¬’l‚Pپ|‚Q‚گ
 پ@پ@پ@
پ@پ@پ@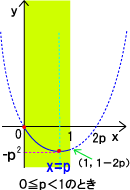 پ@پ@پ@
پ@پ@پ@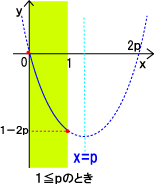
پ@‚إ‚حپAڈم‚ج—ل‘è‚جچإ‘ه’l‚حپHƒOƒ‰ƒt‚ھ‰؛‚ة“ت‚إ‚ ‚é‚©‚çپA•دˆو‚ج’†گSˆت’u‚ً‹«‚ة‚µ‚ؤژ²‚جˆت’u‚ئ”½‘خ‘¤‚جچإ’[‚إچإ‘ه’l‚ً‚ئ‚éپB•ْ•¨گü‚ج‘خڈجگ«‚ة‚و‚èپA•دˆو‚Oپ…‚کپ…1‚ج’†‰›ˆت’u‚ھ‚کپپ![]() پA(ژ²‚کپپ‚گ‚ب‚ج‚إ)پ@پ@
پA(ژ²‚کپپ‚گ‚ب‚ج‚إ)پ@پ@
پ@ƒAپF‚گپƒ![]() ‚ج‚ئ‚«‚کپپ‚P‚إچإ‘ه’l‚Pپ|‚Q‚گپ@
‚ج‚ئ‚«‚کپپ‚P‚إچإ‘ه’l‚Pپ|‚Q‚گپ@
پ@ƒCپF‚گپپ![]() ‚ج‚ئ‚«‚کپپ0,1‚إپ@‚™پپ0پ|2*p*0=0,پ@y=1پ|2*
‚ج‚ئ‚«‚کپپ0,1‚إپ@‚™پپ0پ|2*p*0=0,پ@y=1پ|2*![]() *1=0پ@‚و‚ء‚ؤچإ‘ه’l0
*1=0پ@‚و‚ء‚ؤچإ‘ه’l0
پ@ƒEپF![]() پ„‚گ‚ج‚ئ‚«‚کپپ0‚إچإ‘ه’l0
پ„‚گ‚ج‚ئ‚«‚کپپ0‚إچإ‘ه’l0
پ@‚ـ‚ئ‚ك‚é‚ئپAپ@پ@‚گپƒ![]() ‚ج‚ئ‚«چإ‘ه’l‚Pپ|‚Q‚گپA
‚ج‚ئ‚«چإ‘ه’l‚Pپ|‚Q‚گپA![]() پ…‚گ‚ج‚ئ‚«چإ‘ه’l0
پ…‚گ‚ج‚ئ‚«چإ‘ه’l0
پƒ‹وˆو‘S‘ج‚ھ“®‚‚ئ‚«پ„پ@
ƒOƒ‰ƒt‚ھ‰؛‚ة“ت‚ج‚ئ‚«پA‚”پ…‚کپ…‚”پ{2‚ج‚و‚¤‚ة’è‹`ˆو‚ھ•دگ”‚إ‚ ‚é‚ئ‚«پA‹وٹش‚ج•‚ح‚Q‚إ‚ ‚éپB‚±‚ج‹وٹش‚ج’†‰›ˆت’u‚ئٹضگ”‚جژ²‚جˆت’u‚ً”ن‚ׂؤپAژ²‚ھ‹وٹش‚ج’†‰›‚ج“_‚ئˆê’v‚µ‚ؤ‚¢‚ب‚¢ڈêچ‡پAژ²‚ج”½‘خ‘¤‚ة‚ ‚é’è‹`ˆو‚جچإ’[‚ھچإ‘ه’lپBژ²‚ئ“¯‚¶‘¤‚ج’è‹`ˆو‚ج’[‚ھچإڈ¬’l‚إ‚ ‚éپB
—لپF‚”پ…‚کپ…‚”پ{2‚ة‚¨‚¢‚ؤ‚جٹضگ”‚†(‚ک)پپ2‚ک‚Qپ|4‚ک+3‚جچإ‘ه’l‚l(‚”)‚¨‚و‚رچإڈ¬’l‚چ(‚”)‚ً‹پ‚ك‚وپBپ@
‚†(‚ک)پپ‚Q(‚کپ|1)‚Q+1پ@ژ²‚ح‚کپپ1پA’¸“_‚ح(‚PپA1)پA‚”پ…‚کپ…‚”+‚Q‚ج’†‰›’l‚ح‚”+1
پ@‚کپپ‚”‚ج‚ئ‚«‚ج‚™چہ•W‚ج’l(‚±‚ج‚™‚ھ‚کپپ‚”‚ج‚ئ‚«‚جچإ‘ه’l‚©چإڈ¬’l‚ة‚ب‚é)‚حپA
‚†(‚”)پپ2‚”‚Qپ|‚S‚”پ{3پپ2‚”‚Qپ|4‚”پ{3
پ@‚کپپ‚”+2‚ج‚ئ‚«‚ج‚™چہ•W‚ج’l‚حپA
‚†(‚”+2)پپ2 (‚”+2)‚Qپ|4 (‚”+2)پ{3پپ2‚”‚Qپ{‚S‚”پ{3
پ@چإ‘ه’l‚حپA
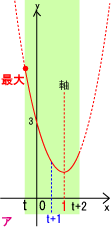
پ@ƒAپF‚”پ{1پƒ1پ@‚·‚ب‚ي‚؟‚”پƒ0‚ج‚ئ‚«پ@‚l(‚”)پپ‚†(‚”)پ@پ©‚کپپ‚”‚ج‚™چہ•W‚ھچإ‘ه’l
پ@ƒCپF‚”پ{1پ†1پ@‚·‚ب‚ي‚؟‚”پ†0‚ج‚ئ‚«پ@‚l(‚”)پپ‚†(‚”+2) پ©‚کپپ‚”+2‚ج‚™چہ•W‚ھچإ‘ه’l
پ@چإڈ¬’l‚حپA
پ@ƒEپF‚”+2پƒ1پ@‚·‚ب‚ي‚؟‚ج‚ئ‚«پ@‚چ(‚”)پپ‚†(‚”+2)
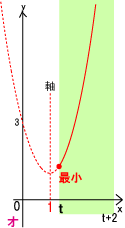
پ@ƒGپF‚”پ…‚Pپƒ‚”+2پ@‚·‚ب‚ي‚؟‚”پ…1‚©‚آ1پƒ‚”+2پ¨پ|1پƒ‚”پ@‚و‚ء‚ؤپAپ|1پƒ‚”پ…1‚ج‚ئ‚«
پ@پ@پ@پ@پ@پ@پ@پ@‚چ(‚”)پپ‚†(1)پ@
پ@ƒIپF‚Pپƒ‚”‚ج‚ئ‚«پ@‚چ(‚”)پپ‚†(‚”)
 پ@پ@
پ@پ@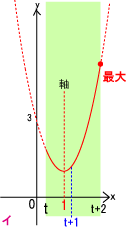 پ@پ@
پ@پ@ پ@پ@
پ@پ@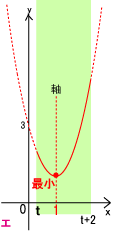
 پ@پ@
پ@پ@
“ڑپFپ@‚l(‚”)پپ2‚”‚Qپ|4‚”پ{3پ@(‚”پƒ0)
پ@پ@پ@‚l(‚”)پپ2‚”‚Qپ{‚S‚”پ{3پ@(‚”پ†0)
پ@پ@پ@‚چ(‚”)پپ2‚”‚Qپ|4‚”پ{3پ@(‚”پƒپ|1)
پ@پ@پ@‚چ(‚”)پپ1پ@(پ|1پƒ‚”پ…1)
پ@پ@پ@‚چ(‚”)پپ2‚”‚Qپ|4‚”پ{3پ@(‚Pپƒ‚”)
پƒƒOƒ‰ƒt‚ھ“®‚ڈêچ‡پ„
—ل‚¦‚خپA‚™پپپ|‚R(‚کپ|‚گ) ‚Qپ{‚Tپi0پ…‚کپ…4پj‚إ‚حپAژ²‚ج•û’ِژ®‚حپ@ْIپپ‚گ‚إ‚ ‚éپB‚گ‚ج’l‚ة‚و‚ء‚ؤپAژ²ˆت’u‚ھ•د‚ي‚éپBچإ‘هپEچإڈ¬‚حپA‚گپ„0پi’èگ”پj‚ئ‚¢‚¤ڈًŒڈ‚إپA
پ–ژ²ْIپپ‚گ‚ھ‹وٹش0پ…‚کپ…4‚ج“à‚©ٹO‚©پ@پ©‚گ‚ئ4‚ج‘هڈ¬پ@(‚گپ„0‚و‚è)
پ@پ–ژ²ْIپپ‚گ‚ھ‹وٹش‚ج“à‚ب‚ç‚خپA‹وٹش‚ج’†‰›‚ة‘خ‚µ‚ؤژ²‚ھچ¶‚©‰E‚©پ@پ©‚گ‚ئ‚Q‚ج‘هڈ¬
پ@‚إŒˆ‚ـ‚éپB
ڈم‹L‚و‚èڈêچ‡•ھ‚¯‚µ‚ؤƒOƒ‰ƒt‚و‚èچإ‘هپEچإڈ¬‚ً‚à‚ئ‚ك‚éپB
—لپFپ@‚گپ„0پi‚گ‚ح’èگ”پj‚ئ‚µ‚ؤپAٹضگ”‚™پپپ|(‚کپ|‚گ) ‚Qپ{‚Sپ@(0پ…ْIپ…2)‚ة‚آ‚¢‚ؤپA‚»‚ج’lˆو‚ً‚گ‚ج’l‚ة‚و‚ء‚ؤڈêچ‡•ھ‚¯‚µ‚ؤ‹پ‚ك‚وپBپ@
پ@پ–‚گ‚حژ²‚ب‚ج‚إپA’lˆو‚ً‚à‚ئ‚ك‚é‚ة‚حژ²ˆت’u‚إ•د‰»‚·‚éچإ‘هپEچإڈ¬‚ً‹پ‚ك‚éپB
پ@پ@‚ـ‚½پA‚±‚ج•ْ•¨گü‚ح‚·‚إ‚ةٹî–{Œ`پF‚™پپ‚پ(‚کپ|‚گ) ‚Qپ{‚‘‚جŒ`‚إ‚·‚ثپBپ@
پ@پ@’lˆو‚ح‚ک‚ج’è‹`ˆو“à‚إ‚†(‚ک)‚ھ‚ئ‚肤‚é’lپi‚™چہ•Wپj‚ج”حˆحپB
پ@ٹضگ”‚™پپپ|(‚کپ|‚گ) ‚Qپ{‚S‚حپ@ڈم‚ة“ت‚جƒOƒ‰ƒt‚إ‚·پBپ@ژ²‚ح‚کپپ‚گپ@
پ@‚ـ‚½‚کپپ0‚ج‚ئ‚«‚™پپ4پ{‚گ‚QپA‚کپپ‚گ‚ج‚ئ‚«‚™پپ4پA‚کپپ‚Q‚ج‚ئ‚«‚™پپ‚گ(‚گپ{4)‚ً‚ئ‚éپB
پ@ڈêچ‡•ھ‚¯پFپ@
پ@پ@پ–ژ²ْIپپ‚گ‚ھ‹وٹش0پ…‚کپ…2‚ج“à‚©ٹO‚©پ¨پ@
پ@پ@پ@پ@پ@پ@پ@0پƒ‚گ‚و‚èپ¨پ@0پƒ‚گپ…2پAپ@2پƒ‚گ(‹وٹش‚جٹO‘¤)
پ@پ@پ–ژ²ْIپپ‚گ‚ھ‹وٹش‚ج“à‚ب‚ç‚خپA‹وٹش‚ج’†‰›‚ة‘خ‚µ‚ؤژ²‚ھچ¶‚©‰E‚©پ@(‹وٹش‚ج’†‰›‚ح1)پ¨پ@
پ@پ@پ@پ@پ@پ@پ@0پƒ‚گپƒ1(‹وٹش‚ج’†‰›‚و‚èچ¶‘¤)پAپ@‚Pپ…‚گپ…2(‹وٹش‚ج’†‰›‚و‚è‰E‘¤)
پ@پ@‚»‚±‚إپA0پƒ‚گپƒ1پA‚Pپ…‚گپ…2پA2پƒ‚گ‚ج‚و‚¤‚ةڈêچ‡•ھ‚¯‚·‚éپB
پ@پ@ژں‚ةٹeڈêچ‡•ھ‚¯‚جƒOƒ‰ƒt‚و‚èچإ‘هپEچإڈ¬‚ً‹پ‚ك‚éپB
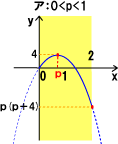
پ@پ@‰؛گ}‚و‚èپAƒAپF0پƒ‚گپƒ1‚ج‚ئ‚«’lˆو‚حپ@‚گ(‚گپ{4)پ…‚™پ…‚S
پ@پ@پ@پ@پ@پ@پ@ƒCپF‚Pپ…‚گپ…2‚ج‚ئ‚«’lˆو‚حپ@0پ…‚™پ…4
پ@پ@پ@پ@پ@پ@پ@ƒEپF2پƒ‚گ‚ج‚ئ‚«’lˆو‚حپ@0پ…‚™پ…‚گ(‚گپ{4)
 پ@پ@پ@
پ@پ@پ@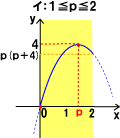 پ@پ@پ@
پ@پ@پ@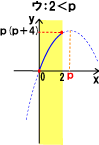
پƒچإ‘هپEچإڈ¬‚©‚çŒWگ”Œˆ’èپ„
پ@پ–چإ‘ه¥چإڈ¬‚ب‚ç‚Qژںٹضگ”‚ًٹî–{Œ`‚™پپ‚پ(‚کپ|‚گ) ‚Qپ{‚‘پ@‚جŒ`‚ة‚·‚éپBچإ‘ه¥چإڈ¬‚حژ²‚جˆت’u‚ة‚و‚ء‚ؤŒˆ‚ـ‚é‚©‚ç‚إ‚·پBپ@‚ـ‚½پA‚پ‚جگ³•‰‚ھ•s–¾‚ج‚ئ‚«پA‚پپ„0پA‚پپپ0پA‚پپƒ0ڈêچ‡•ھ‚¯‚µ‚ؤچإ‘ه’lپAچإڈ¬’l‚ًچl‚¦‚و‚¤پBٹب’P‚ةƒOƒ‰ƒt‚ً•`‚¢‚ؤژ²‚ئ‚ج‹——£‚إ’è‹`ˆو‚ج’[‚ھچإ‘ه¥چإڈ¬‚ب‚ج‚©‚ًŒˆ‚ك‚éپB‚ـ‚½ڈêچ‡‚ة•ھ‚¯‚½‚çپAڈêچ‡‚جڈًŒڈ‚جٹm”F‚àگ³ٹm‚ةچs‚¤پB
—لپFپ@ٹضگ”‚†(‚ک)پپ‚پ‚ک‚Qپ{‚Q‚پ‚کپ{‚‚(پ|‚Qپ…‚کپ…1)‚جچإ‘ه’l‚ھ6پAچإڈ¬’l‚ھ2‚ج‚ئ‚«’èگ”‚پپA‚‚‚ج’l‚ً‹پ‚ك‚وپB
پ@‚†(‚ک)پپ‚پ(‚کپ{‚P) ‚Qپ|‚پپ{‚‚پ@پ@ژ²‚کپپپ|1
 پ@ پ@
پ@ پ@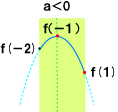 پ@پ@پ@
پ@پ@پ@
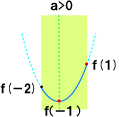
پ@‚پپ„0‚ج‚ئ‚«پ@پ@ƒOƒ‰ƒt‚و‚èپA‚کپپپ|1‚إچإڈ¬پA‚کپپ1‚ج‚ئ‚«چإ‘ه‚ئ‚ب‚éپB
پ@پ@پ@‚µ‚½‚ھ‚ء‚ؤپA‚†(پ|1)پپ‚پپ|‚Q‚پپ{‚‚پ¨پ@‚†(پ|1)پپپ|‚پپ{‚‚پپ2
پ@پ@پ@پ@پ@پ@پ@پ@پ@‚†(1)پپ‚پپ{‚Q‚پپ{‚‚پ¨پ@‚†(1)پپ‚R‚پپ{‚‚پپ6
پ@پ@پ@‚±‚ê‚ً‰ً‚‚ئپ@‚پپپ‚PپAپ@‚‚پپ‚Rپ@‚±‚ê‚ح‚پپ„0‚ً–‚½‚·پB
پ@‚پپپ0‚ج‚ئ‚«پ@‚†(‚ک)پپ‚‚پ@ˆê’è‚ئ‚ب‚èپA–â‘è‚جڈًŒڈ‚ً–‚½‚³‚ب‚¢پB
پ@‚پپ„0‚ج‚ئ‚«پ@ƒOƒ‰ƒt‚و‚èپA‚کپپپ|1‚إچإ‘هپA‚کپپ1‚ج‚ئ‚«چإڈ¬‚ئ‚ب‚éپB
پ@پ@پ@‚µ‚½‚ھ‚ء‚ؤپA‚†(پ|1)پپ‚پپ|‚Q‚پپ{‚‚پ¨پ@‚†(پ|1)پپپ|‚پپ{‚‚پپ6
پ@پ@پ@پ@پ@پ@پ@پ@پ@‚†(1)پپ‚پپ{‚Q‚پپ{‚‚پ¨پ@‚†(1)پپ‚R‚پپ{‚‚پپ2
پ@پ@پ@‚±‚ê‚ً‰ً‚‚ئپ@‚پپپپ|‚PپAپ@‚‚پپ5پ@‚±‚ê‚ح‚پپƒ0‚ً–‚½‚·پB
پ@پ@پ@پ@پ@“ڑپFپ@پ@‚پپپ‚PپA‚‚پپ‚Rپ@‚ـ‚½‚حپ@‚پپپپ|‚PپA‚‚پپ‚T
گ”ٹw–عژں‚ضپ¨