<2次関数の決定>
条件:頂点または軸が与えられたとき → y=a(x-p) 2+q
:頂点の情報がないとき。または3点の情報がわかる場合 → y=ax2+bx+c
:ⅹ軸との交点が2つわかるとき → y=a(x-α)(x-β)
:ⅹ軸と接するとき → y=a(x-p) 2
*aがポイント!
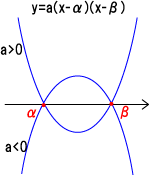
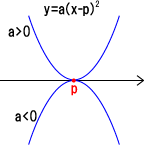
例:
グラフの頂点が(2、-3)で点(1、-5)を通る2次関数をもとめよ。
*頂点が与えられたので、y=a(x-p) 2+q (a≠0)でスタートしよう。
y=a(x-2)2-3 ←グラフが点(1、-5)を通るから、
-5=a(1-2) 2-3 よって、a=-2 ←a≠0を満たす。
よって、y=-2(x-2) 2-3 すなわち、y=-2x2+8ⅹ-11答
例:
3点(3、0)、(6、0)、(2、-8)を通る放物線の方程式を求めよ。
*3点ではあるが、2点がⅹ軸との交点なので、y=a(x-α)(x-β)でスタートしよう。
y=a(x-3)(x-6) → -8=a(2-3)(2-6) → a=-2
よって、y=-2(x-3)(x-6) → y=-2x2+18x-36 答
例:
放物線y=-2x2+9x-18 を平行移動したもので、ⅹ軸と2点(-1,0) 、(2,0)で交わる。
*平行移動しても2次の係数は変わらないので、-2である。
また、ⅹ軸と2点で交わるから、y=a(x-α)(x-β)でスタートしよう。
y=-2(x+1)(x-2) すなわち、y=-2x2+2x+4 答
例:
y=2x2-4x+3 を平行移動したもので、2点(-2,-11)、 (1,4)を通る。
*もとのグラフの式より、2次の係数が2である情報がもらえた。
頂点の情報はないので、y=ax2+bx+cよりスタートしよう。
よって、-11=2・(-2) 2+b(-2)+c → -2b+c=-19
4=2・(1) 2+b(1)+c → b+c=2
b=7、c=-5、 よって、y=2x2+7x-5 答
例:
グラフは放物線y=x2-x-2を平行移動したもので、点(2,3)を通り、その頂点は直線y=3x-1上にある。このような2次関数を求めよ。
*問題に頂点はy=3x-1とあるから、
基本形y=a(x-p) 2+q 頂点の座標(p、q)よりスタート。
頂点(p、q)が直線y=3x-1上にあるので、その座標は(p、3p-1)とおける。
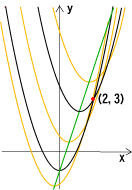 また平行移動しても放物線の2次の係数はa=1のままである。求める2次関数は、
また平行移動しても放物線の2次の係数はa=1のままである。求める2次関数は、
y=(x-p) 2+3p-1 ・・・・①
このグラフが(2,3)を通るから、
3=(2-p) 2+(3・2)-1 → p2-p=0 → p(p-1)=0
よってp=0、1
このpの値をそれぞれ①に代入して、求める2次関数は、
y=(x-0) 2+3・0-1 → x2-1
y=(x-1) 2+3・1-1 → y=(x-1) 2+2 → y=x2-2x+3
答 x2-1 と y=x2-2x+3
<最大・最小からの決定>
2次関数はグラフが対称になっているので、2次の係数が正の場合は、頂点が最小値となる。係数が負の場合は頂点が最大値である。ここに、範囲が定められると、場合分けにより求められる。最大・最小より、2次関数をもとめるためにどの式からスタートするかは問題より読み取っていこう。
例題:
次の条件に適する2次関数を求めよ。
①x=1のとき最小値2をとり、x=3のときy=6となる。
②y-1≦ⅹ≦5において、x=-1のとき最小値-7、x=3のとき最大値9をとる。
解①:
①は定義域がなく、最小値をとるのだから、グラフが下に凸(a>0)である。
ⅹ=1のとき最小値2をとるから、頂点に関する情報なので,
求める2次関数は基本形y=a(x-p) 2+qよりスタートする。
よって、y=a(x-1) 2+2 (a>0) ←y=2=a(1-1) 2 +2
更に、x=3のとき、y=6なので、上の式に代入し
6=a(3-1) 2+2 → 6=4a+2 よって、a=1 (a>0を満たす)
よって、 y=(x-1) 2+2 すなわち、y=x2-2x+3 答
解②:
x=3は-1≦ⅹ≦5の定義域内にある。その値は定義域の端ではなく、且つ最大値ということから、a<0のグラフの頂点である事がわかる。
よって、求める2次関数は基本形y=a(x-p) 2+qよりスタートする。
y=a(x-3) 2+9 (a<0)とおける。
軸x=3は定義域-1≦ⅹ≦5の右寄りにあるから、x=-1で最小値y=-7をとる。
-7=a(-1-3) 2+9 よって、a=-1 (a<0を満たす)
したがって y=-(x-3) 2+9 すなわち、y=-x2+6x 答
<連立方程式の解法>
●連立方程式などで、文字が多い式のときは、等しい数量を作って=(イコール)で結び、一文字を消去して、残りの文字式について解けば良い。
●連立3元一次方程式の解法も、一文字を消去して、残りの2文字についての連立方程式を導き、そこで更に一文字消去しある一文字についての値を求め、その値を使い、他の2文字を導きだす。
例: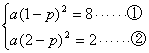 →②を4倍し、①②の右辺を8で等しくして、=で結ぶ。
→②を4倍し、①②の右辺を8で等しくして、=で結ぶ。
a(1-p)2=4a(2-p)2 両辺をaで割る。
(1-p)2=4(2-p)2 → -3p2-14p+15 →
→ (3p-5)(p-3)=0 ∴p=![]() 、3
、3
p=![]() のとき①に代入して、
のとき①に代入して、![]() →
→ ![]() =8 ∴a=18
=8 ∴a=18
p=3のとき①に代入して、a(1-3)2=8 → 4a=8 ∴a=2
<2次関数のグラフと2次方程式>
2次関数y=ax2+bx+cのグラフとⅹ軸との共有点のⅹ座標は、2次方程式ax2+bx+c=0の実数解(D≧0)である。
この方程式が実数解をもつかどうかはD=b2-4acの符号で決まる。
復習:
一般形 ax2+2x+c=0 (a、b、cは実数、a≠0)
の形で表される方程式をⅹの2次方程式という。
2次方程式とは、Y=0のときのxの値をもとめる式(解は実数解がないときもある)
解説:
2次関数 y=ax2+bx+c・・・・・①
①のグラフがⅹ軸と共有点(α、0)を持つとき
↑言い換えると、グラフがx軸と点(α、0)で接するか交わるという意味ですよ。
0=aα2+bα+c・・・・・・・② が成り立つ。 ←グラフが点(α、0)を通る。
したがって、x=αは
2次方程式 ax2+bx+c=0・・・・・③の実数解である。
逆に、2次方程式③が実数解x=αをもつとき、②が成り立つから、点(α、0)は2次関数①のグラフとⅹ軸の共有点である。
一般に次のことがいえます。
y=f(x)のグラフとⅹ軸の共有点のⅹ座標は、
方程式f(x)=0の実数解である。
お助け:
「共有点」とは「交点」と考えて差し支えありません。D=0のグラフはⅹ軸に「接する」といい、正確には「交わる」とは言えないので、その「共有点」を「接点」と呼ぶようにしています.
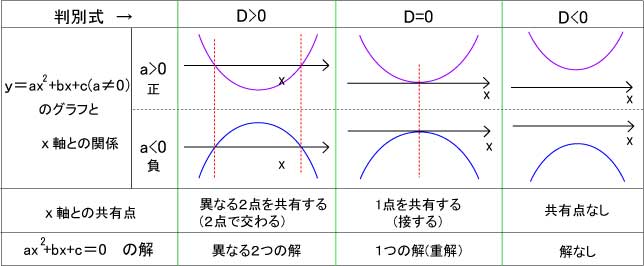
2次の係数が正・負のどちらであってもⅹ軸の共有点は一致(赤の破線みよ)するから係数の符号は関係ない。それについて少し説明しよう。
2次関数y=ax2+bx+cのグラフはD=b2-4acとし、ⅹ軸のp、y軸のqとおいてみる。ax2+bx+cの平方完成により
ax2+bx+c=![]() より、頂点の座標を(p、q)とすると、pは
より、頂点の座標を(p、q)とすると、pは![]() 、qは
、qは![]() です。このy座標qの値によって(ⅹ軸に接するとか、正か負によって)、ⅹ軸の共有点が決まる。もっと解り易くいえば、
です。このy座標qの値によって(ⅹ軸に接するとか、正か負によって)、ⅹ軸の共有点が決まる。もっと解り易くいえば、
y座標の![]() ですが、a>0のときにD>0であれば、
ですが、a>0のときにD>0であれば、![]() なので下に凸のグラフで頂点のy座標は負になる。また、a<0のときにD>0であれば
なので下に凸のグラフで頂点のy座標は負になる。また、a<0のときにD>0であれば![]() なので上に凸のグラフで頂点のy座標は正になる。上の表を見てください。どちらの場合でも、ⅹ軸の共有点(交点)は同位置にあります。(赤の点線上にⅹ軸の交点があるでしょう?)2次の係数が正・負のどちらであってもⅹ軸の共有点は一致する(赤の破線みよ)から係数の符号は関係ないのである。aの正・負に関係なく、Dの符号よって上記表のような関係がある。
なので上に凸のグラフで頂点のy座標は正になる。上の表を見てください。どちらの場合でも、ⅹ軸の共有点(交点)は同位置にあります。(赤の点線上にⅹ軸の交点があるでしょう?)2次の係数が正・負のどちらであってもⅹ軸の共有点は一致する(赤の破線みよ)から係数の符号は関係ないのである。aの正・負に関係なく、Dの符号よって上記表のような関係がある。
ポイントのまとめ
ここでのポイントは2次関数y=ax2+bx+cのグラフとⅹ軸との共有点であるから、共有点のx座標は2次方程式2次方程式ax2+bx+c=0の実数解である。そしてこの方程式が実数解をもつかどうかは判別式D=b2-4acの符号で決まる。
y=f(x)のグラフとⅹ軸の共有点のⅹ座標は、
方程式f(x)=0の実数解である。
例題:y=2x2+3x-1はⅹ軸と共有点をもつか?もつ場合、その座標を求めよ。
2x2+3x-1=0を解くと、
![]() ←D=32-4・2・(-1)=17なので D>0
←D=32-4・2・(-1)=17なので D>0
よって、ⅹ軸との共有点は2つある。その座標は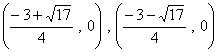 答
答
例題:y=x2-2x+1はⅹ軸と共有点をもつか?もつ場合、その座標を求めよ.
x2-2x+1=0を解くと、(x-1) 2=0 ←D=(-2) 2-4・1・1=0 D=0
これより、x=1(重解)
よって、ⅹ軸との共有点は1個。 その座標は(1,0)答
例題:y=3x2-2x+1はⅹ軸と共有点をもつか?もつ場合、その座標を求めよ。
D=(-2) 2-4・3・1=-8なので D<0
したがって、ⅹ軸との共有点はない。答
<2次関数の決定②>
グラフが次の条件を満たす2次関数をそれぞれ求めよ。
(1)放物線y=-2x2を平行移動させたもので、ⅹ軸と2点(-2,0)、(1,0)で交わる。
(2)ⅹ軸との交点が(-1,0)、(3,0)で、y軸との交点が(0、-2)である。
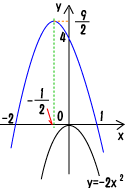 *2問とも2点がⅹ軸との交点なので、y=a(x-α)(x-β)でスタートしよう。
*2問とも2点がⅹ軸との交点なので、y=a(x-α)(x-β)でスタートしよう。
(1)の解
y=a(x+2)(x-1) →y=-2x2の2次の係数は平行移動しても変化しない→
a=-2 したがって y=-2(x+2)(x-1) 答
*グラフの参考:
y=-2(x+2)(x-1) → y=-2x2-2x+4 *x=0のときy=4ですね。
y=-2(x2+x)+4→y=-2(x+![]() )2+4+
)2+4+![]() → y=-2(x+
→ y=-2(x+![]() )2+
)2+![]()
(2)の解
y=a(x+1)(x-3) → この2次関数は点(0、-2)を通るから、この点でのⅹ、y座標を代入する → -2=a(0+1)(0-3) → ![]()
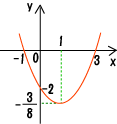 したがって、
したがって、![]() 答
答
*グラフの参考:
![]() →
→ ![]() *x=0のときy=-2ですね。
*x=0のときy=-2ですね。
→![]()
数学目次へ→