•s“™ژ®
•s“™چ†‚ً‚à‚؟‚¢‚ؤگ”‚ج‘هڈ¬ٹضŒW‚ً•\‚µ‚½ژ®پBپ@•s“™چ†‚جچ¶‘¤‚جگ”‚âژ®‚ًچ¶•سپA‰E‘¤‚جگ”‚âژ®‚ً‰E•سپA—¼‘¤‚ً—¼•س‚ئ‚¢‚¤پB
پƒ•s“™ژ®‚ج‰ًپ„
‚½‚ئ‚¦‚خ•دگ”ْI‚ة‚آ‚¢‚ؤ‚ج•s“™ژ®‚إپA‚»‚ج•s“™ژ®‚ًگ¬‚è—§‚½‚¹‚é‚و‚¤‚ب‚ک‚ج’l‚ً‚»‚ج•s“™ژ®‚ج‰ً‚ئ‚¢‚¤پB•s“™ژ®‚ج‰ً‚ج‚·‚ׂؤ‚ً‹پ‚ك‚éژ–‚ً•s“™ژ®‚ً‰ً‚‚ئ‚¢‚¤پB
پƒ‚Pژں•s“™ژ®پ„
•دگ”‚ک‚ة‚آ‚¢‚ؤ‚ج•s“™ژ®‚إپA‚پ‚کپ„‚‚پAa‚کپƒ‚‚پA‚پ‚کپ†‚‚پA‚پ‚کپ…‚‚‚ج‚¢‚¸‚ê‚©‚جŒ`‚ة‚ب‚é•s“™ژ®‚ً‚ک‚ة‚آ‚¢‚ؤ‚جˆêژں•s“™ژ®‚ئ‚¢‚¤پB
پƒ‚Pژں•s“™ژ®‚ج‰ً‚«•ûپ„
‚PپF‚©‚ء‚±‚ً‚ح‚¸‚·
‚QپFŒWگ”‚ج•ھگ”پAڈ¬گ”‚ح—¼•س‚ة“K“–‚بگ”‚ًٹ|‚¯پAŒWگ”‚ًگ®گ”‚ة‚·‚éپB
‚RپFˆعچs‚·‚éپB•دگ”‚ک‚جچ€‚حچ¶•س‚ةپB’èگ”چ€‚ح‰E•س‚ةپB
پ@پ@’èگ”چ€‚ئ‚حپF•û’ِژ®‚إ–¢’mگ”‚ًٹـ‚ـ‚ب‚¢چ€پB‚ـ‚½پA‘½چ€ژ®‚إ•دگ”‚ًٹـ‚ـ‚ب‚¢چ€پB
‚RپF—¼•س‚ً‚»‚ꂼ‚êگ®—‚µ‚ؤپA‚پ‚کپ…‚‚پ@‚ب‚ا‚جٹب’P‚ةŒ`‚ة‚·‚éپB
‚SپF—¼•س‚ًپ@•دگ”‚ک‚جŒWگ”‚پ‚إٹ„‚éپ@پi‚پ‚جگ³•‰‚إ•s“™چ†‚جŒü‚«‚ھ•د‚ي‚é‚ج‚إ’چˆسپj
پƒ•s“™ژ®‚جٹî–{“Iگ«ژ؟پ„
ƒAپF‚Q‚آ‚جژہگ”‚پپA‚‚‚ة‚آ‚¢‚ؤ‚حپA‚پپ„‚‚پA‚پپپ‚‚پA‚پپƒ‚‚‚ج‚R‚آ‚جٹضŒW‚ج‚ا‚ê‚©‚P‚آ‚¾‚¯‚ھگ¬‚è—§‚آ
ƒCپF‚پپ„‚‚پA‚‚پ„‚ƒپ@پثپ@‚پپ„‚ƒ
ƒEپF‚پپ„‚‚پ@پثپ@‚پپ{‚ƒپ„‚‚پ{‚ƒپA‚پپ|‚ƒپ„‚‚پ|‚ƒ
ƒGپF‚پپ„‚‚پA‚ƒپ„0پ@پثپ@‚پ‚ƒپ„‚‚‚ƒپAپ@![]()
ƒIپF‚پپ„‚‚پA‚ƒپƒ0پ@پثپ@‚پ‚ƒپƒ‚‚‚ƒپA![]()
پ–پ@•s“™ژ®‚إ‚حپA—¼•س‚ة“¯‚¶•‰‚جگ”‚ًٹ|‚¯‚½‚èپAٹ„‚ء‚½‚è‚·‚é‚ئ•s“™چ†‚جŒü‚«‚ھ•د‚ي‚è‚ـ‚·پB
—لپ@5پ„3پ@پ@—¼•س‚ة4‚ًٹ|‚¯‚éپثپ@‚Tپ~4پ@پ„پ@‚Rپ~‚S
—لپ@5پ„3پ@پ@—¼•س‚ةپ|‚S‚ًٹ|‚¯‚éپثپ@‚Tپ~(پ|4)پ@پƒپ@‚Rپ~(پ|‚S)پ@پ¨پ@پ|20پƒپ|12
—لپ@پ|3‚کپ„15پ@پ@—¼•س‚ًپ|3‚إٹ„‚éپثپ@ْIپƒپ|5
—لپ@‚`پƒ‚aپƒ‚bپ@پC‚کپƒ‚™پƒ‚ڑ‚ب‚ç‚خ
پ@پ@پ@‚`پ{‚کپƒ‚aپ{‚™پƒ‚bپ{‚ڑپ@پ@‚ـ‚½پAپ@‚`پ|‚ڑپƒ‚aپ|‚™پƒ‚bپ|‚ک
—لپ@0.5‚کپ{0.9پ„‚کپ|0.2
پ@پ@—¼•س‚ة10‚ًٹ|‚¯‚ؤپ@5‚کپ{9پ„10‚کپ|2پ@پ¨پ@5‚کپ|10‚کپ„پ|2پ|9پ@پ¨پ@پ|5‚کپ„پ|11
پ@پ@—¼•س‚ًپ|5‚إٹ„‚ء‚ؤ‚کپƒپ@![]()
پ–پuپ@‚`پ†‚aپ@پv‚حپu‚`پ„‚aپ@‚ـ‚½‚حپ@‚`پپ‚aپv‚ئ‚¢‚¤‚±‚ئپB
پƒژہگ”‚ج‘هڈ¬‚ئچ·‚جگ³•‰پ„
پ@پ@‚پپ|‚‚پ„0پ@پجپ@‚پپ„‚‚پ@پ@پ@پ@پ@پ@پ@پ@‚پپ|‚‚پƒ0پ@پجپ@‚پپƒ‚‚
پƒگ³‚جگ”‚ج‘هڈ¬‚ئ•½•û‚ج‘هڈ¬پ„
پ@پ@‚پپ„0پA‚‚پ„0‚ج‚ئ‚«پ@‚پ2پ„‚‚2پ@پجپ@‚پپ„‚‚پ@پ@
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@‚پ2پ†‚‚2پ@پجپ@‚پپ†‚‚پ@
پƒکA—§•s“™ژ®پ„
کA—§•s“™ژ®‚ج‰ً‚«•ûپF
‡@‚»‚ꂼ‚ê•تŒآ‚ة•s“™ژ®‚ً‰ً‚
‡AچإŒم‚ة‚·‚ׂؤ‚ج•s“™ژ®‚ج‰ً‚ً‚ ‚ي‚¹‚ؤ‹¤’ت”حˆح‚ً‚à‚ئ‚ك‚é
پ@پ@—لپ@5‚کپ|2پ…‚کپ…3‚کپ{2
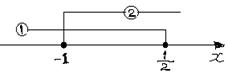
پ@پ@‚T‚کپ|2پ…‚کپ@پ¨پ@‚S‚کپ…2پ@پ¨پ@‚کپ…پ@![]() ¥¥¥¥‡@
¥¥¥¥‡@
پ@پ@‚کپ…3‚کپ{2پ@پ¨پ@پ|‚Q‚کپ…2پ@پ¨پ@‚کپ†پ|1¥¥¥¥‡A
پ@پ@پ@پ@پ@‡@‚ئ‡A‚ج‹¤’ت”حˆح‚ً‚à‚ئ‚ك‚ؤپ@پ|1پ…‚کپ…پ@![]()
پ@پ@پ@—لپ@
پ@پ@‡@پ@6‚کپ|1پ…3‚کپ{9پ@پ¨6xپ|3‚کپ…10پ@پ¨پ@![]()
پ@پ@‡Aپ@—¼•س‚ة3ٹ|‚¯‚ؤپ@پ¨پ@‚U‚کپ{9پ„5پ|2‚کپ|12پ@پ¨پ@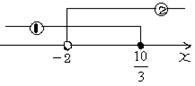
پ@پ@پ@پ@پ¨پ@‚U‚کپ{2‚کپ„پ|16پ@پ¨8‚کپ„پ|16پ@پ¨پ@‚کپ„پ|2پ@
‡@‚ئ‡A‚ج‹¤’ت”حˆح‚ً‚à‚ئ‚ك‚ؤپ@پ|2پƒپ@![]() پ@
پ@
پƒ•ھگ”•s“™ژ®پ„پ@
پ@پ@![]() پ@پ@
پ@پ@
پ@—لپ@![]() پ@پ„0پ@پ¨پ@‚کپE(‚کپ|‚Q)پ„0پ@پ@پ@پ@پ@پ©—¼•س‚ة‚ک2‚ًٹ|‚¯‚é‚ئ•s“™چ†‚جŒü‚«‚ح“¯‚¶‚ة‚ب‚éپ@
پ@پ„0پ@پ¨پ@‚کپE(‚کپ|‚Q)پ„0پ@پ@پ@پ@پ@پ©—¼•س‚ة‚ک2‚ًٹ|‚¯‚é‚ئ•s“™چ†‚جŒü‚«‚ح“¯‚¶‚ة‚ب‚éپ@
پ@
پƒ‘ٹ‰ء‘ٹڈو•½‹د‚ج•s“™ژ®پ„
پ@پ@پ–‚پ‚کپ{پ@![]() پ@‚جŒ`‚ج•ھگ”‚جچإڈ¬’l‚ً‹پ‚ك‚é‚ئ‚«‚ة–ً—§‚آپB
پ@‚جŒ`‚ج•ھگ”‚جچإڈ¬’l‚ً‹پ‚ك‚é‚ئ‚«‚ة–ً—§‚آپB
پ@پ@![]() پ@پ@پ@پ@پ¨—¼•س‚ة‚Q‚ًٹ|‚¯‚ؤپ¨پ@پ@پ@پ@
پ@پ@پ@پ@پ¨—¼•س‚ة‚Q‚ًٹ|‚¯‚ؤپ¨پ@پ@پ@پ@![]() پ@پ@
پ@پ@
پ@پ@پ@‘ٹ‰ء•½‹دپ@پ@پ@‘ٹڈو•½‹د
—لپ@ْIپ{پ@![]() پ@‚جچإڈ¬’l‚ئ‚»‚ج‚ئ‚«‚جْI‚ج’l‚ً‹پ‚ك‚éپB
پ@‚جچإڈ¬’l‚ئ‚»‚ج‚ئ‚«‚جْI‚ج’l‚ً‹پ‚ك‚éپB
پ@پ@ْIپ{پ@![]() پ@پ†‚Q
پ@پ†‚Q![]() پ@پ†‚Q
پ@پ†‚Q
پ@پ@![]() پ@پ†‚Q‚ئ‚¢‚¤‚±‚ئ‚حپ@
پ@پ†‚Q‚ئ‚¢‚¤‚±‚ئ‚حپ@![]() پ@پپ2‚إ‚à‚ ‚éپB—¼•س‚ةْI‚ًٹ|‚¯‚ؤ(“™ژ®‚ب‚ج‚إ‚ک2‚ً‚µ‚ب‚‚ؤ‚و‚¢)
پ@پپ2‚إ‚à‚ ‚éپB—¼•س‚ةْI‚ًٹ|‚¯‚ؤ(“™ژ®‚ب‚ج‚إ‚ک2‚ً‚µ‚ب‚‚ؤ‚و‚¢)
پ@پ@پ@
پ@پ@‚ک‚Qپ|‚Q‚کپ{‚Pپپ0پ@پ@پ¨پ@پ@(‚کپ|‚P) ‚Qپپ0پ@پ@پ@‚و‚ء‚ؤ‚کپپ1