��Βl
���Ȃ݂ɐ�Ƃ́A�����Â����邱�ƂȂ��A�Ɨ��I�ŁA���ꎩ�̂ɂ��������S�ł��邱�Ƃ��Ӗ�����B
�����ƕ����̊W�ŁA������0.23�́@�����ł�23/100�ł���킷�B���̕������A0.23�Ƃ������Ɓu100�̂�����23�v�Ƃ������A����ɂ��̃C���[�W��`���̂��\�Ƃ�������ȑ��݂ł���B�Ǝ��͎v���Ă܂��B���������ł͂Ȃ������𐔊w�ŕ\�������i�Ƃ��āA�������傫�����v���K�悤�Ȋ��I�����̐�Βl������B�ƁA�O�u�����Ă����܂��B����ȕ\�����Ă悢�̂��B�B�B�Ԉ���Ă�ł��傤��?
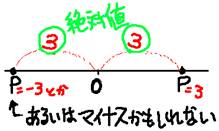
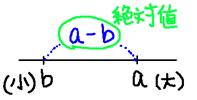
��Βl�Ƃ� �Q�_�Ԃ̋����܂��́A���A�傫�����Ӗ�������́B
��`�ł́A��������ŁA���_�O�Ɠ_�o�̊Ԃ������̂������B
������A�_�o�����ł����ł���Βl�͓��l�ɂȂ�(�}�Q�l)��
�Ƃ������Ƃ́A
��Βl�]�����]�̒l�͐��ƕ��̗����ɂ����̂��I
��Βl�L���́b�@�b�ł��B
�@�@�@�@���|�T�̐�Βl�����߂�Ƃ��́A
�@�@�@�@�@�@�@|�|5|���|(�|5�j��5�@�@�Ƃ����悤�Ɏ��ɂ���킷�B
�@�@�@�@����Βl��3�@�Ȃ̂́A�|3�@�Ɓ@3�@�̂Q����B
�@�@�@�@�@�@�@|�|3�b���|�i�|3�j��3
�@�@�@�@�@�@�@�b3�b��3
��蕶���ɐ�Βl�b�|5�b�Ȃǂ��o�Ă����炻�̐�Βl�L���b�b���͂����Ȃ��Ƃ����܂���B
��Βl���͂����ɂ̓O���t�A�������A�s�������ꂼ��ɓ��L�̕��@������܂����A��{�͎��̍l�����ł��B
�b�`�b �̐�Βl�̂͂������@���@��Βl�̓����̐����ŏꍇ����������B
�q���g�F�@�@| |�̒������������̏ꍇ�i��̗�̂悤�ȁj�A���̒l����Βl�ł���B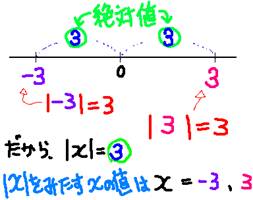
��Βl�b�|3�b�̓����͕��ł���ˁB���̏ꍇ�̐�Βl��3�ɂȂ邯�ǁA
�b�@�b�̓��������Ȃ�}�C�i�X�L���������Ȃ��Ƃ����Ȃ���3�Ƃ������̐��ɂȂ�܂���B
��肩����(�|)�~(�|)��(+)����������Ń}�C�i�X���|�����B
�����ł͂���Ȋ����ŕ��̕����������܂��B
����ā@�b�|�R�b���|(�|�R)��3
���́A��Βl�����߂�̂ł͂Ȃ��A���̐�Βl�̌��ł���b�b�̒��̘b�B
����||�̒��̕����̒l�����Ƃ߂�ɂ͂ǂ����邩�H
���������ꍇ�͉E�ӂ̐�Βl�������������肷��B�E�}���Q�l�ɂ��ĂˁB
��Βl�b�w�b���R�@�����w�̒l�́@�w���|�R,�R
���b�T�b��|�|2�b�̐�Βl�����Ƃ߂Ă݂悤�B
�@|�|2|�@= �b�@�@���������Ȃ̂Ł|(�|�Q)���Q
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
���F�b���Q
�@�@�@�b5�b���b�@�@�T�̐�Βl�́A�T
���F�b��5
 ����Βl���C���[�W�I�ɗႦ�遄
����Βl���C���[�W�I�ɗႦ�遄
�j�������Ă��܂��B
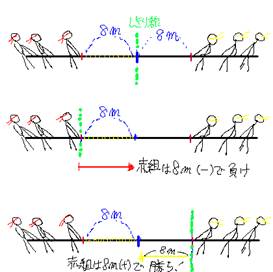
���̂W�l�Ƃ��������͒n�ʂ̎d���(�ΐ�)��
�j�̒��S(��)�Ƃ𐂒��Ɉʒu���킹���A
���S����8�l�̋����ɂ���ڈ�̐ԕR�܂ł̋����B
�����ł́A�����̐ԑg�������݂Ă݂悤�B
�W�l���������(�{)�Ə����B
�t�ɂW�l����������(�|)�ƕ����B
���̂W�l�Ƃ����傫���͈������荞�܂�Ă��A
���������Ă������͕ς��Ȃ��B
�����ǁA�����i�����j������B(�W�l�������E�W�l��������ꂽ)
���̂W�l�͐�ΓI�ɕω����Ȃ��B
�v���X�����́|8�l��}�C�i�X������8�l�Ƃ������̂�
8�l�Ƃ����傫�� (��Βl)������̂ł��B
���̑傫�����Βl�Ƃ����܂��B
�b�w�b���W�@�@�w���|�W�A�W
�ǂ��A�K�C�e���A�k�܂�Ȃ������B���ꂪ��Βl�H�I
�g���ŗ��������ƁA�`�N160�����A�a�N170�����Ƃ���B�@
���̍���10�����B�@����͓�l�̐g���̍��̑傫���ł���B
�a�N����ɂ��āA�`�N�́|10�����ł���B�@|�|10|
�`�N����ɂ��āA�a�N��+10�����ł���B�@�b10�b
���̍����傫��(��Βl)��10�����ł���B�����ĕ��̒l�ɂ͂Ȃ�Ȃ��B
|�|10|���|10�@�@�ƂȂ������Ⴂ���Ȃ����H
�|10�Ƃ����傫���ł͎ړx�Ɏg���Ȃ�����Ǝv���Ă������B
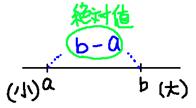
�Q�_a��b�̐�Βl�����߂Ă݂悤�B
�i�������̂Ƃ��j�b���|���b= �}�i���|���j
�i�������̂Ƃ��j�b���|���b= �}�i���|���j
������`�A�����������Βl�Ȃ�
���_�|5�Ɠ_3�̐�Βl��|�R�|(�|�T)�b��8�@�@
���_�|�P�Ɠ_�|�V�ł́A|�|�P�|�V�b���|(�|�W)��8
�Ƃ������ƂŁA����ǂ͋t�ɍl���Ă݂悤�B
��Βl�b�w�b��5�@�ł���Ƃ������Ƃ́H�@
�܂�A�b�|�T�b��5�܂��́A�b5�b��5�ł�����̂ŁA
�b�w�b= 5�@�Ƃ́A�]�͐����̗����������Ƃ������Ƃ�����A�@�����́@�]���@�}5
�@
����Βl���܂ޕ������E�s�����̉���
�������A�s�����͐�Βl���܂肵�܂��B
��Βl�b�w�b�i��Βl�͏�ɐ��j�����]�̒l�͈ȉ��̊�b�`�C�a�C�b���Q�l�ɂ��Ă݂Ă��������B
�ȉ��̊�b�`�C�a�C�b�͂ƂĂ��d�v�ł��B�o����悤�ɁI
�@�������b�͐�Βl�̉��Ő��̐����̂���ł݂Ă��������B
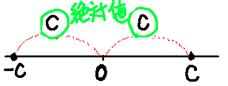
��b�`�b�]�b��C �����]�̒l�́@�]=�}C
�@�@�����ł����Βl�b�w�b������B��Βl�͐��ƕ��̗�������B
�@����āA�w�̒l�͂b(���̐���)�C�|�b(���̐���)�ł���B
�@�@��1�@�b�]�b���R
�b�w�b���R���݂����w�̒l�́@�\�\���@���F�]���}�R
�@�@��P���@|�|�R�b���@�|(�|�R)���R
�@�@�@�@
��b�a�b�]�b��C �����w�̒l�́@�|�b���]���b
�s����������A�l��f��ł��Ȃ���ˁB
���̏ꍇ�̂w�́A�i���ł��鐳�̐����j�b��菬�����l�ł���B
�ɒ[�ȗ�ł����ƁA�i���ł��鐳�̐����j�b���Q�ł���Ƃ��܂��B
�Q��菬����������0.9�Ƃ�0.05�Ƃ��i���̐����j�B
�Q��菬�����l�ŁA�b�w�b��0.9�Ƃ���ƁA0.9��2�ł���B
�w�͐����̗��������̂ŁA�w���|0.9�A0.9�Ȃ̂ŁA�ق�A�͈͓��ɂw������ł���B
��2�@�b�w�b��10
�@ �b�w�b��10���݂����w�̒l�́@�\�\���@���F�|10���w��10
��b�b�b�w�b��C �����w�̒l�́@�w���|�b�C�b���w
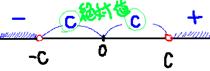
��Ŏ����ƁA�b4.5�b��3�Ƃ��܂��B4.5��3�ł���B
�w�͐����̗��������̂ŁA�w���|4.5�A4.5�Ȃ̂ŁA�ق�A�͈͓����ˁB
���̗����̐}�ɂ��Ă͂߂Ă����B��1�ł͂b���R�Ƃ��Ă݂ĂˁB
��3�@�b�w�b���Q �b�w�b���Q���݂����w�̒l�́@�\�\���@���F�]���|2�A2���w
���@���b�w�b��8 ���F�]���}8 ���b�w�b��5�@�@���F�|�Q���]�A�Q���w
���b�|15�b �ˁ@�|(�|15)��15�@���F�b�|15�b��15
���@�ˁ@|�|6|�@�� �|(�|6)��6�@���F�b�Q�|8�b��6
���b�w�|�R�b���Q�@ �q���g�F���̌`�́@�b�w�b���b�@����āA�w���|�b�C�b���w
�b�͂Q�Ȃ̂ŁA�w�|�R���|�Q�A�Q���w�|�R�@�䂦�Ɂ@�w��1�C5���w�@��
��4�b1�|�w�b���R�@�q���g�F�b1�|�w�b�́b�w�|�P�b�ƕό`�ł���B
�b�w�|1�b���@![]() �@�@�@���@�|�@
�@�@�@���@�|�@![]() �@���w�|�P���@
�@���w�|�P���@![]() �@�@���@�@
�@�@���@�@![]() �@���w���@
�@���w���@![]() �@�@��
�@�@��
�����܂ł̂܂Ƃ�
�b�w�b�� ����(�����݂����Ȃ���)�@�@�ϐ��w�̐�Βl�����ƕ��̂Q�R����.
��Βl���k�܂ʂQ�_�Ԃ̋����@������I
����Βl���������̏ꍇ��
��������́A��Βl���������̏ꍇ�ǂ���邩�݂Ă݂悤.
�b�w�b = �����@�ł͂Ȃ��A�@�b�w�b=
�a(�a�͕�����)�̂悤�ȏꍇ�̂��ƁB
�������I�w���}�a�ł͓������킩��Ȃ���B
�O����Ƃ��āA�O���傫���Ɓu���̐��v�C�O��菬�����Ɓu���̐��v�ɕ������܂��B0�͐����ǂ������ɂ����Ă��悢�B
���̏ꍇ�������邩�H
�b�w���܂ޕ������b���@�w�@���܂ޕ������̏ꍇ�A��Βl�̓����̐����ŏꍇ����������Βl���͂����Ȃ��Ƃ����Ȃ��B
��Βl�͐����̗���������̂͂����킩��ł��傤�H��Βl�b�w�b��5�@�̂Ƃ��A�b�|�T�b��5�܂��́A�b5�b��5�ł�����̂ŁA
�b�w�b= 5�@���݂����]�̒l�́A�����̗��������邩��ł��B
�w�Ƃ��������͐��������킩��Ȃ��̂ŁA��������~�X���N�������˂܂���B
|�Q�w�|�R|���w�@�Ő������܂��傤�B
�Q�w�|3���w�@���@�w��3�Ƃ��Ă悢���H�@�@�@�������A�����܂���B�@�Ȃ����H
�����Ȃ��Βl�L�����͂������Q�w�|3�@�Ƃ��Ă͂����Ȃ��̂ł��B�Q�w�|3�@�����ł���\�������邩��ł��B
���̏ꍇ�A|�Q�w�|�R|���|(�Q�w�|�R)���|�Q�w�{�R�@�Ƃ��Ȃ�����n�܂�܂���ˁB
����ŁA�|�Q�w�{�R���w�@���@�|�R�w���|�R�@���@�w��1�@�ق�A���܂ňႤ�ł���B����āA|�@|�̒��̐��ƕ��ŏꍇ�������čl���Ȃ��Ă͂Ȃ�Ȃ��B
|�@|�̒��̕����͐���������Ȃ����A����������Ȃ��B���ꂪ�n�b�L���킩��Ȃ����痼���̏ꍇ���l���Ȃ��Ƃ����Ȃ��B
�ꍇ����������A��Βl�̉��͐��������ł���B
���̂Ƃ��A�ꍇ�����̏����Ɖ��͈̔͂���������Ă��邩�K���m�F����B���������Ȃ������͉��ɂ͂Ȃ�Ȃ��B
���ƕ��̗����̃p�^�[���ʼn��͈̔͂����Ƃ߂��킯������A���̐��͈̔͂ƕ��͈̗̔͂������ꍇ�����������ɂȂ�͓̂��R���ˁB
��Βl���܂ޕs�����̂Ƃ��͐����̉������킹��悤�ɁB
�͈͂��_�u��Ȃ��悤�ɂ��邽�߁B���y�[�W�̈�ԉ��ɗႪ����B
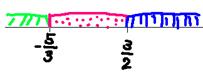
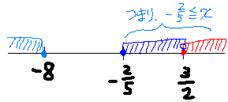
����@�b�Q�`�|�R�b���` �@
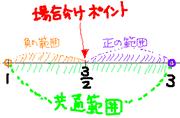 �@�@�q���g�F��Βl�����̐����́A�`���@
�@�@�q���g�F��Βl�����̐����́A�`���@![]() �@�̂Ƃ����A�`���@
�@�̂Ƃ����A�`���@![]() �@�̂Ƃ����ɂȂ�ˁB
�@�̂Ƃ����ɂȂ�ˁB
�`���@![]() �@�̂Ƃ��A�Q�`�|�R���`�@�䂦�ɂ`��3�@������@
�@�̂Ƃ��A�Q�`�|�R���`�@�䂦�ɂ`��3�@������@![]() �@���`��3�����@
�@���`��3�����@
�`���@![]() �@�̂Ƃ��A�|(�Q�`�|�R)���`�@�䂦�ɂ`���P�C����ĂP���`���@
�@�̂Ƃ��A�|(�Q�`�|�R)���`�@�䂦�ɂ`���P�C����ĂP���`���@![]() �@�����A
�@�����A
�s�����̏ꍇ�Ō�ɇ@�ƇA�����킹���͈͂������@�P���`���R�@��
�������
�o���Ă���ł��傤���A��Βl�b�|15�b�̓����͕��ł���ˁB
���̏ꍇ�̐�Βl��15�ɂȂ邯�ǁA�b�@�b�̓��������Ȃ�}�C�i�X�L���������Ȃ��Ƃ����Ȃ��ƂP�T�Ƃ������̐��ɂ͂Ȃ�Ȃ���B
��肩����(�|)�~(�|)��(+)����������Ń}�C�i�X���|�����B
����ŁA��Βl�̒l�͏�ɐ��̐����ł���̂��B
���Ȃ��́A�R��������ĕ����Ă���̂����āA�^�̐l����ɁA
���̐l�̈ʒu(��)�͂R���[�g���@�O�̐l�̈ʒu(��)�͂Q�D�T���[�g�����Ă���
��ΓI�ȋ������݂��邩��킩��ł���H�i�܁A���ڂ��g���Čv��Ƃ��āj
�Ă��A���̑O��i�����j�̋����͗����Ƃ����̋����ł���ˁH���ڂŌv���̂�����B
�Ƃ��낪�A�Q�_�Ԃ̋������}�C�i�X�̋������āH�H�H������A��Βl�́{�A���łȂ���B
������A�A�̐̑��������͕�������A�}�C�i�X�Ŋ|���Ȃ��ᐳ�̐�Βl�͂łĂ��Ȃ��B
�ꍇ������������A���̏����������m�F������I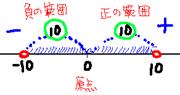
�@�@�@�s�����̏ꍇ�́A�ꍇ���������l���ŏI�I�ɍ��킹��
�b�w�b��10���݂����w�̒l�́@�\���@���F�|10���w��10�@
�܂茴�_�O����ɁA��~���͈͓̔��ɂ���Ƃ����Ӗ�
�ꍇ�����ł́A��Βl�L���������Ȃ�͂����̂͂��@�x(��Βl���������̏ꍇ�A���̋L�����|���Đ�Βl�L�����͂��������ɂ���̂Œl���Ⴄ�̂�)�Ƃ������ƂŁA�����̊�����_�O�ł͂Ȃ��A�w���������Ƃ肤��l����ɂ��Ă����Ƃ����Ƃ��낪�ꍇ�����̃|�C���g���낤���H
���|�Q�w�|�S|���w�{�P�@��b�b���K�p�ł��Ȃ��̂ŏꍇ����
 (�w���Q�̂Ƃ���)�@
(�w���Q�̂Ƃ���)�@
�@�@�@�@�@�@�@�@�@�|(�Q�]�|�S) ���w�{�P�@���@�w���P�@(�����w���Q����)
(�Q���w�̂Ƃ���)
�@�@�@�@�@�@�@�@�@ �Q�w�|�S���w�{�P�@���@�w��5�@(�����w���Q����)
����b�Q�w�|3�b��4�@�@�R���́A��Βl�������̌`�������@
�Q�w�|�R���}4�@�@����āA�@�w���@![]() �@�C�@
�@�C�@![]()
����@![]() �@�@�R���͂Q�悷��ƕK�����ɂȂ�̂ł��̂܂܂͂�����
�@�@�R���͂Q�悷��ƕK�����ɂȂ�̂ł��̂܂܂͂�����
�@![]() �@�@���@(�Q���{�X)(�Q���|�R)���O�@�����|
�@�@���@(�Q���{�X)(�Q���|�R)���O�@�����|![]() �@�A�@
�@�A�@![]()
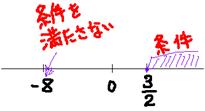
����@|�w�|3| �w�|�R����b�`���K�p�ł��Ȃ��̂ŏꍇ��������B
�A�F|�w�|3|���w�|�R����������R�̂Ƃ��A�b�b������
�C�F���|(�w�|�R)���|�w�{�R�����������R�̂Ƃ��A�b�b������
�s�����ł͂Ȃ��̂œ��͍��킹�Ȃ��Ŋe�X���̒ʂ�
���|�w�|�Q|�||�w�|�R| �R��������B�w�͂P�łQ�̐�Βl�b�b�Ɏg�p����Ă���B
�A�F�����Q�̂Ƃ��A�����Ƃ��� �|(�w�|�Q)�|{�|(�w�|�R)}���|�w�{�Q�{�w�|�R���|�P
�C�F�Q���w���R�̂Ƃ��A�Е��͐��A����͐�
�w�|�Q�|{�|(�w�|�R)}���w�|�Q�{�w�|�R���Q�w�|�T
�E�F�w���R�̂Ƃ��@�����Ƃ��� �w�|�Q�|�w�{�R���|�P
�s�����ł͂Ȃ��̂œ��͍��킹�Ȃ��Ŋe�X���̒ʂ�
����@![]() �b�b�̒��͕��ɂȂ�̂Ł|�P���|����
�b�b�̒��͕��ɂȂ�̂Ł|�P���|����
�@![]() �@ ���@
�@ ���@![]() �@���|�S�{�@
�@���|�S�{�@![]()
����b�b�w�b�|2�b �b�w�b����͂����B�w���O�ŁA�O����ɂ���
�A�F�w���O�̂Ƃ��@���Ȃ̂ŁA�͂����Ƃ��Ɂ|�P���|����
�@�b�b�w�b�|2�b�@���@�b�|�w�|�Q�b _____�X�Ɂb�b�ŏꍇ��������
�`�F�w���|2�̂Ƃ����ɂȂ�̂ŁA���̂܂܂͂���
�b�|�w�|�Q�b���@�|�w�|�Q��
�a�F�|2���w���O�̂Ƃ����ɂȂ�̂ŁA�|�P���|����@�w���O�̓A�̏����ł���
�b�|�w�|�Q�b���|(�|�w)�|�Q�@���w�{�Q��
�C�F0���w�̂Ƃ��@���Ȃ̂ł��̂܂܂͂���
�b�b�w�b�|2�b�@���b�w�|�Q�b�@�@_____�X�Ɂb�b�ŏꍇ��������
�`�F�O���w��2�̂Ƃ����ɂȂ�̂ŁA�|�P���|����
�b�w�|�Q�b���|�w�{2��
�a�F 2 ���w�̂Ƃ����ɂȂ�̂ŁA���̂܂܂͂���
�b�w�|�Q�b��X�|�P��
���|�Q�w�|1|���R�w�|�S
�A�F�Q�w�|�P���O�̂Ƃ��A�܂�w���@![]() �@�̂Ƃ����Ȃ̂ł��̂܂܂͂���
�@�̂Ƃ����Ȃ̂ł��̂܂܂͂���
�Q�w�|�P���R�w�|�S �@3�w�|2�w���|1�{4 �@�@�w��3�@(�����w��![]() �@����)
�@����)
�C�F�Q�w�|�P���O�̂Ƃ��A�܂�w���@![]() �@�̂Ƃ����Ȃ̂ł��̂܂܂͂���
�@�̂Ƃ����Ȃ̂ł��̂܂܂͂���
�|(�Q�w�|�P)���R�w�|�S �@����Ăw���P�@(�����w���@![]() ���������Ȃ�)������s�K
���������Ȃ�)������s�K
�ȏ�ʼn��͂w���R�̂�
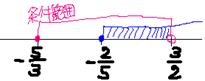
����b�Q�w�|�R�b���b�R�w+5�b �e�ꍇ�������Ƃɋ��ʔ͈͂����Ƃ߁A�s�����Ȃ̂ōŌ�ɑS�����킹��B
�Q�l�F�@![]() �@���P�D�T�@�@�|�@
�@���P�D�T�@�@�|�@![]() �@���|1.666�@�@����āA�@
�@���|1.666�@�@����āA�@![]() �@���@�|
�@���@�|![]()
 �A�F�����@�w��
�A�F�����@�w��![]() �̂Ƃ����ӂƂ����Ȃ̂ł��̂܂܂͂����܂�
�̂Ƃ����ӂƂ����Ȃ̂ł��̂܂܂͂����܂�
�Q�w�|3���R�w�{5�@�@�w���|�W�@(���������Ȃ�)
�@�@�@�@�@�@�@�@�@�@�@�@�@�@����Ăw��![]() ����@
����@
 �C�F�����@�|
�C�F�����@�|![]() ���w��
���w��![]() �̂Ƃ�
�Q�l�F�|
�̂Ƃ�
�Q�l�F�|![]() ���|�O�D�S
���|�O�D�S
�|(�Q�w�|3) ���R�w�{�T ����������Ăw���|![]()
����� �|![]() ���w��
���w��![]() �����A
�����A
 �E�F�����@�w���|
�E�F�����@�w���|![]() �̂Ƃ��@���ӂƂ����ɂȂ�
�̂Ƃ��@���ӂƂ����ɂȂ�
�@�@�@�@�|(�Q�w�|3) ���|(�R�w�{�T)
�@�@�@�@�@�@�@�R���������Ăw���|8�@����B�@�i���������j
�s�����Ȃ̂Ň@�A�B�����킹���͈͂�����A�w���|![]() �@�A�w���|8
�@�A�w���|8
|1�|�w|�ł��邪�A
���ɂw��0.8�ƒu���Ă݂āA|�P�|0.8�b��|0.2|��0.2
���ɂw���|�Q�ƒu���Ă݂āA|�P�|(�|2)|���b3�b ��3
|�w�|1|�����l��
���ɂw���O�D�W�ƒu���Ă݂āA|0.8�|1�b���b0.2�b��0.2
���ɂw���|�Q�ƒu���Ă݂āA|�|�Q�|1|��|�|�R|�@������͂����Ƃ��́|(�|�R)���R
�ȏ���A|�W�|�w|�̂悤�Ȍ`���b�b�����Ł|�P���|�����b�w�|�W�b�ƕϊ��ł���