|
補足 その2 データ圧縮について | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
コンピューターの世界では、様々な目的でデータの量をもっと小さくする必要に迫られることがあります。例えば最もよくあるのは通信を行う場合です。 現在のモデムはだいたい28800bps(1秒間に28800ビット=3600バイト)の転送速度ですが、その速度でもしフロッピーディスク一枚分のデータを送ろうとすると、6〜7分の時間がかかってしまいます。これがもし市外通話だったりしたら、それだけでも電話代がかなりかかります。 またその他にもハードディスクの容量を節約したいとか、限られた資源を有効に使いたいことはよくあります。 そのためたぶんLHAのような圧縮ソフトを利用された方は多いと思います。それではいったいどうやってデータの量を減らしているのでしょうか? データ圧縮とはデータ圧縮とはすなわちデータのサイズをどうにかして元より小さくする方法です。 もちろん半分に切り落としてしまえば半分になりますが、これでは意味がありませんね。すなわち、元のデータの情報はそっくり残したまま、サイズだけを小さくできないかというのが問題です。 一体こんなことができるのでしょうか? 非常に多くの場合にこれは可能なのです。それはどういう場合かというとデータに何らかの規則性がある場合です。もしデータに規則性があるのであれば、それを利用してデータサイズを小さくすることができるのです。 データ圧縮方法1 ランレングスでは具体的にはどんな方法を使うのでしょうか?まず下の例を見てください。これはある画像データの一部を16進数で表した物です。
これを利用しない手はありません。上のデータは次のように言うことができるわけです。 00が1個、D4が20個、00が1個、59が20個、00が1個、B7が20個... 以上の内容を以下のように表示するという規則を作っておけばデータは下のようになります。
この方法をランレングス圧縮といい、圧縮の中では最も基本的な方法です。 単純なランレングスだとうまく行かない例上のように簡単なやり方でも結構小さくなるデータもあるのですが、例えば今度は下のような例はどうでしょう?
00〜03がただひたすらずらっと並んでいるデータです。これを上のやり方で単純に処理すると下のようになってしまいます。
なんと元のサイズより2倍も増えてしまいました! もちろん00 01 02 03をひとまとめにしてそれが何個というように表現することもできますが、データの内容は様々です。例えば00〜02が単に並んでいると変更しただけでもうこの手は使えません。 でもこのデータにはとにかく規則性がありますよね。どうにかならないのでしょうか? データ圧縮方法2 ハフマン符号化そこで別なところに目を付けます。前の例ではよく考えてみるとデータには00から03までの4種類の値しかありません。0から3までなら2進法で表せば2桁で表示できます。すなわち 0=00 1=01 2=10 3=11 そこで00 01 10 11を詰めて並べて1B(00011011=1B)と表現してみましょう。すると前のデータは単に
ということになります。バイトにこだわらずにビット単位で考えてしまうわけです。こうすればデータ量は1/4になりました! といっても00〜03だけのデータなんて滅多にないんじゃないか?と思われるかもしれません。もちろんその通りです。 しかしデータに現れる数値の頻度は普通は偏っています。例えば有名なところでは、英語に現れるアルファベットで最も多いのはEであるというのがありますね。 ほとんどどのようなデータでもこのように各値の出現頻度はたいてい異なっているのです。 ではこの出現頻度の違いをどう利用するのでしょうか? それは今までは各データの値が例えば1バイトの長さを持っているように書いてきました。しかしここではそうではなく、各データの長さがデータごとに異なっていてもいいとします。 そして出現頻度の高い値に二進法で表せば短い数値を、出現頻度の低い値には長い数値を割り当てた変換表を作っておくのです。この表を元にデータを変換すれば、全体としてはデータ量が小さくなると考えられます! 例えばデータが以下の頻度順で現れるとします。それに対して表のように二進法の値を割り振ります。
次に以下のようなデータがあったとします。
2進法データを間を詰めて書いてしまえば
見るともとは11バイトあったデータが5バイトになっています! このような方法でデータの圧縮をすることをハフマン符号化法といいます。この方法だとデータの並びがどうであっても、頻度の偏りさえあれば圧縮が可能です。従ってこの方法はデータ圧縮の中では最もよく使われている方法です。 ちなみにこの方法の最大のミソはデータと2進符号の対応表をいかにうまく作るかというところにあります。そのために様々な方法があるのですが、本当に難しくなってしまうのでここでは割愛します。 その他にも圧縮の方法はたくさんありますが、どの方法も必ずデータの中の規則性を検出してそれを利用して圧縮するところは同じです。 圧縮したデータをさらに圧縮したら?さてそれではこんな便利な圧縮法があるのであれば、圧縮したデータをさらに圧縮すればどんどんサイズが小さくなっていくのでは?と思った人はいませんか? 残念ながらそれは無理です。というのは、データの中に規則性がなければ圧縮は不可能なのです。すなわち全くランダムに0〜255が現れるデータはどうやっても圧縮できません。そしてデータ圧縮をした後のデータは必ずデータの規則性は失われて、ランダムな数値列にどんどん近づいていきます。 このために、もうこれ以上圧縮できない限界が常に存在します。 圧縮のあまり効かない例
データ圧縮方法3 不可逆圧縮:JPEGさて以上の二つはデータ圧縮の中でも可逆圧縮と呼ばれるカテゴリーに属します。可逆とはすなわち圧縮したデータを元に戻したら(これを展開とか解凍とかいいます)最初のデータと全く一致するからそういわれるわけです。 しかし世の中には不可逆圧縮というものもあります。こういうと次のような疑問がわくでしょう。 データを元に戻せないのであれば圧縮した意味がないのではないか? もちろん一般的にはその通りです。でも特殊な応用では元に戻らなくてもほとんど実用上差し支えないこともあるのです。そのいい例がビットマップ画像データの圧縮です。 画像データに要求されることはそれを「見た」ときに前と同じに見えることです。画像の場合は見た目の区別がつかなければ、データの内容が少々前と違っていても、ほとんどの場合は問題ありません。 みなさんもたぶんご存じでしょうがJPEGというグラフィックのフォーマットがあります。これがこの不可逆圧縮を行っています。 では実際にはどういうことをするのでしょうか? 写真のような画像をよく見ると、色合いや明るさががかなり連続的に変化しています。 そこで一部分を取り出して明るさのグラフを書いてみます。すると以下のような感じになるでしょう。 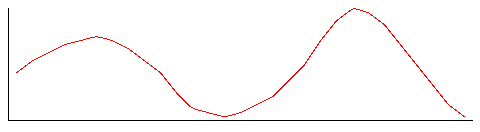 このグラフにフーリエ変換という方法を使います。これは工学系の人ならばたぶん悪夢に出てくるのではないかと思いますが、とにかくものすごく便利な手法なのです。 みなさんはたぶん昔、関数のグラフというのを描いたことがあるでしょう?例えばy=x2というグラフは放物線になりました。関数の式が分かれば関数のグラフを描くのは簡単です。しかし上のグラフのような場合、でたらめに描いたグラフですから、このグラフを表す関数なんて元々存在しません。従ってこのグラフを再現しようとすると、各座標点の数分のデータが必要になります。 ところがこういういい加減な曲線であっても、このフーリエ変換を使えば単なる三角関数の合成で表されてしまうのです。 従って上のいい加減な曲線が
というように書けてしまうのです。難しい?そんなことはどうでもいいんです。とにかく式で書けるということが重要なんです。 関数の式が分かればその関数のグラフを描くことができます。すなわち元のデータと上の関数の式は同じ内容を現しているといってもいいわけです。 しかも重要なところは曲線の大まかな部分であれば最初の数項だけで十分なのです。すなわち
この式を表現するにはいちいち式を書かなくても、a1,a2,〜c3の九つの数を指定するだけで十分です。最初はたくさんあったデータがこれだけになってしまったわけです。 みなさんの中にもしかしたら実際にJPEGのデータを作ったことがある人がいるかもしれません。そのときに品質係数というのを設定しませんでしたか?係数を小さくすると画像はきれいだけどサイズは大きくなり、大きくするとその逆になりましたね。この係数は実は上の式をどの程度で切り捨てるかということに関与しているのです。 しかしながらこうして変換したこと自体や、後ろの方の式を切り捨ててしまったことで、もちろん元のデータとは変わってしまっています。これがこの方法の不可逆性の由縁です。 これで得られたデータにさらに前のランレングスやハフマン符号化を利用すれば結果はさらに小さくなるでしょう。 また実際のJPEGでは人間の眼の特性をうまく使います。人の眼は明るさにはかなり敏感ですが、色相の違いには意外と鈍いのです。 そこで各ピクセルの色データをRGBで現す代わりに、明度、赤み、青みの3つの値に変換しておきます(そういう変換式があるんです)。そして明度のグラフを上のようにフーリエ変換した結果はなるべく後ろの項までとっておき、赤みと青みに関してはさっさと切り捨ててしまうようにします。するとさらに圧縮率は上がります。 ちなみにJPEGの場合は基本前提として色合いや明るさがなめらかに変化するということがあります。このため非常に不連続にそれが変わるような画像では、あまりきれいに圧縮できません。例えばCGアニメ画像などは輪郭線がはっきりしていますが、JPEGはこういう画像を圧縮するのは苦手です。 しかし写真のような画像であれば逆に非常にきれいに仕上がります。 |