望遠鏡のカタログの読み方〜有効径、集光力、極限等級、分解能、有効最高倍率
●有効径

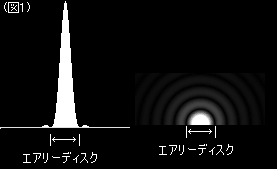
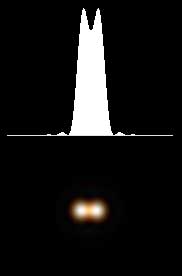
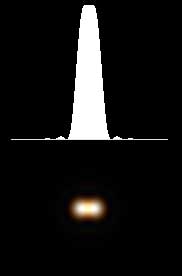
簡単に言ってしまうと、対物レンズや主鏡の大きさのことです。単に「口径」とも言います。望遠鏡は有効径が大きいものほど高性能です。 　星の光は淡いので、たくさん光を集める必要があります。また、解像度を稼ぐには、口径が大きいほど有利です。 　一般に、望遠鏡や超望遠レンズでは、有効径とレンズの前玉の直径はほぼ等しくなります。 　なるべく大きな口径のものを選びたいものです。(値段も高くなりますが…) 　口径が大きいほど、高性能なのは確かなのですが、大きい分だけ重量が増してきて、組み立て・撤収が面倒になってきます。初めて望遠鏡を持つ初心者の場合は、私なら、あえて「口径8cmの屈折望遠鏡」を勧めます。 　8cmあれば、月のクレーターはもちろん、惑星(金星の満ち欠け、火星は最接近時に限りますが大シルチスなどの模様、木星の模様やガリレオ衛星、土星の輪など)は充分に見えます。星雲星団も代表的なものはわかります。 2006/07/10

●カメラレンズの有効径

「有効径は、レンズ直径にほぼ等しい」と言うと、「広角レンズは視野レンズのために有効径よりレンズ径が大きいんだよ」と必ずツッコミが入るので、その辺の話。(今まで数回言われた。知ってるって。) 　広角レンズでは広い視野を一度に写す必要から、レンズ正面ばかりでなく斜めから来る光も取り入れるために有効径よりはるかに大きなレンズが使われます。 中望遠の85mmF2.0と、広角の28mmF2.0。いわゆる「前玉」の直径は約45mmで、ほぼ同じ。 開放絞りの状態で正面から見た状態。どちらもF値が2なので、85mmの有効径は42.5mm、28mmの有効径は14mmになる。広角レンズの有効径は前玉よりずっと小さい。 　焦点距離28mmでF値が2のレンズの場合、理屈の上ではレンズ直径は14mmあれば充分なのですが、広角レンズは、その名の通り、広い角度を一度に撮影する必要から、斜めから来る光も受け入れられるよう、絞り位置から離れるほどレンズ直径を大きくしていく必要があります。 斜めから見た場合。広角レンズは広い範囲を写すので、斜めでも開口径は、ほぼ円形を保っている。望遠レンズは正面しか写さないので、横から来る光を取り入れるような設計はされていない。 　たとえば、85mmと言えば、普通、中望遠のレンズになりますが、中判カメラでは標準レンズとなる焦点距離です。『標準レンズ』とは、およそ画角が60度となるようなレンズを示すからです。 　ところが、35mmフィルム用の85mmでは35mmフィルムに写せるだけの画角しかない(画角が狭い)ので、中判カメラには(取り付けることができたとしても、周辺まで写らないため)使うことができません。 　一方、中判カメラ用の85mmは、大きなフィルムにも対応できるよう、より広い画角を持っています。同じ85mmでも(設計によりますが、一般に)中判カメラ用に使われるレンズは、大きくなります。 　…余談でした。 2006/07/10

●集光力

肉眼の瞳孔の面積(最大直径7mmなので、約38.5平方mm)に対して、望遠鏡の主鏡の面積が何倍に当たるのかを示す値です。主鏡の有効径をD[mm]とすると、 　集光力＝D2÷49 で求めます。 　口径が大きいほど集光力が大きくなり、より明るく見えます。 　つまり、有効径が大きいものほど高性能です。 なぜそんな式になるかと言うと、 　円の面積＝半径×半径×π ですので、 　瞳孔の面積＝π×(7mm÷2)2 　主鏡の面積＝π×(D÷2)2 その面積比は、 　主鏡の面積÷瞳孔の面積 ですので、 　＝(π×(D÷2)2)÷π×(7÷2)2 円周率で約分して 　＝(D÷2)2÷(7÷2)2 二乗を中に入れて、 　＝(D2÷22)÷(72÷22) 　＝(D2÷4)÷(72÷4) 四分の一をまた約分して 　＝(D2)÷(72) できあがり。 　＝D2÷49 　というワケで、副鏡やスパイダーの遮蔽、ガラスの表面反射や内部損失、鏡面の吸収による損失分は含まれていません。 2006/07/31

●極限等級

その望遠鏡で、どこまで暗い星が見えるかを等級で示した数値です。主鏡の有効径をD[mm]とすると、 　極限等級＝1.77 + 5 log D で求めます。logは、常用対数で、底は10です。logという関数は、高校で習います。 　これも、有効径が大きいほど極限等級が大きくなり、高性能になります。 　計算のやりかたは別に記載しましたので、『それゆけ迷走光学』の方を参照してください。 　簡単に言うと、肉眼では6等星まで見えます。1等級の差は約2.51倍。 　つまり、集光力が2.51倍の望遠鏡を使うと見た目の等級がすべて1等級だけランクアップします。3等星は見かけ上、2等星になります。そして、7等星(見えない)が6等星(かすかに見える)に見えてきます。 　ですから、集光力が2.51倍大きくなると、極限等級は1等級大きくなります。 　この調子で、 　集光力が2.51倍のさらに2.51倍(6.3倍)なら2等級ランクアップで8等星、 　集光力が2.51倍の2.51倍の2.51倍(15.8倍)なら3等級ランクアップで9等星… 　まで見えるということになります。 2006/07/31

●分解能

どこまで接近した等光二重星を二重星と見分けられるかを示す指標です。 　一般にドーズの限界が用いられていて、 　　ε＝116[秒]÷D[mm] 　で求めます。計算式を見ての通り、口径が大きくなるほど微細なものが見分けられる事になります。 　どれほど超高精度の望遠鏡を作っても無制限に詳細を見分けられる訳ではありません。これは、光が波の性質を持つためです。 　光が集中する部分をエアリーディスクといい、エアリーディスク直径は光学系のF値をF、調べる光の波長をλ[mm]とすると、無遮蔽・無収差の光学系の場合、 　D＝2.88λF となります。 もし、光が波の性質を持たず、どこまでも詳細に見分けられると仮定すると、実際の恒星の見かけの大きさ(視直径)は、エアリーディスク直径の数百分の一程度という大きさになります。 　さて、等光二重星があった場合、どこまで離れた二重星までを見分けられるのかという指標が分解能です。 　ところが、『何をもって二重星を見分けられたと言えるのか』によって、いくつかの学説があります。 レーリーリミット(レーリーの限界) 　ε＝128[秒]÷D[mm] 　エアリーディスクの半径の長さだけ離れた時点で解像限界とするものです。数式の上で解像限界を決めやすい利点はありますが、現実にはもっと狭くても分離可能です。 ドーズリミット(ドーズの限界) 　ε＝116[秒]÷D[mm] 　ドーズという天文学者が経験則から導き出した分離限界値で、一般にこれが天体望遠鏡の分解能として採用されています。 　最近の高性能対物レンズや、超解像技術によって、これ以上の解像度も出せるとされてます。 スパローリミット(スパローの限界) 　ε＝100[秒]÷D[mm] 　２つの星の光の合成をしたとき、全くピークがなくなった時点で限界とするものです。こうなると、もはやいかなる手段を使っても分離することはできません。 　 2006/07/31

●有効最高倍率

最高倍率の限界を示す倍率で、一般に口径をmmで表した程度の倍率となります。たとえば、口径80mmなら80倍が、口径120mmなら120倍が最高倍率の限界になります。 　ただし、その2倍程度までは実用範囲と言われていて、口径80mmなら160倍あたりまで、口径120mmなら240倍あたりまでなら実用に耐えられます。 　ただし、それ以上の倍率では、像は暗くなり、ボケていく一方になるため、その倍率を有効最高倍率と呼びます。 　分解能の所で触れた、エアリーディスクですが、倍率が低ければ全くの点にしか見えません。 　しかし、どんどん倍率を上げていくと、次第にエアリーディスクが円盤状に見えてきます。 　こうなると、そこから先はいくら拡大しても像が大きくなるだけで詳細はわかりません。そして、どんどん像が暗くなります。 　↑これは、二重星を超高倍率で見た場合を想定しています。いくら倍率が高くても像が肥大して暗くなるだけで、二重星かどうかは判別が困難(=シャープには見えない)です。 　この『ここから先はいくら拡大しても無駄』となる、目安の倍率が有効最高倍率です。 　仮に、同じ星を、口径が4倍大きい望遠鏡で見ると、このようになります。 　さきほどのものと同じ倍率ですが、星像は格段に明るくなり、しかも二重星であることがハッキリわかりますね。 2006/07/31

[戻る]