n sin i=n'sin i'
です。
【補足】
スネルの法則が、なぜそうなるかについては、いろいろな証明方法があるようですが、ホイヘンスの原理による場合は、こうです。
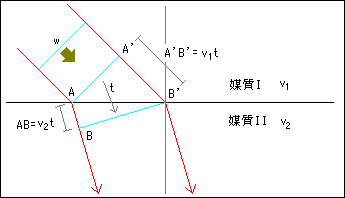
ある平面波wが進行しているとき、波の一端がAに接した瞬間と、時間tだけ経過して、もう一方の端がB'に接した瞬間の状態を図に示しました。
媒質Iの波の進行速度がv1、媒質IIの波の進行速度がv2なので、同じ時間tの間に素元波が進んだ距離は、媒質IIの長さAB=v2t、媒質Iの長さA'B'=v1tとなります。
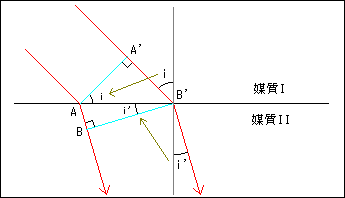
波面は、必ず光線と直交しますから、入射角iは角A'AB'、射出角i'は、角AB'Bと等しくなります。
直線AB'は、互いの三角形で共有していますから、

本当は、この証明方法で出てくるのは、相対屈折率(媒質Iと媒質IIの屈折率の比=n'/n)です。
この相対屈折率を、媒質Iを真空と見立てて絶対屈折率(真空中の屈折率)を出し、その決定した一方の絶対屈折率から媒質IIの絶対屈折率を求め、もう一度組み直す必要があるのですが、その辺は割愛します。
高校物理で教えてくれるから、先生から教わってね。