色収差量の正体

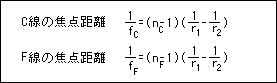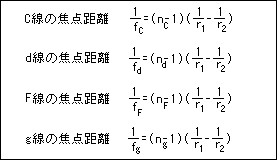
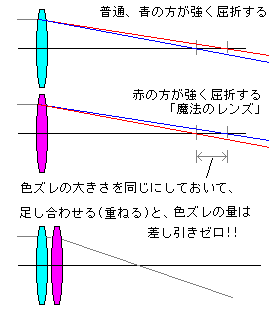
同じ光学ガラスでも波長によって屈折率が違うので、波長ごとに焦点の位置が変わってしまいます。これが、色収差の正体です。 　一般に、単レンズの焦点距離と言う場合は、d線での焦点距離を言います。 　眼視用の光学設計では、基本的にC線(赤、656nm)、d線(黄、587nm)、e線(緑、546nm)、F線(青、486nm)g線(青、435nm)、h線(紫、404nm)の６色の屈折率について検討しますが、一般に、そこまで複雑にしても答えが出ないのがオチなので、C線(赤■)、d線(黄■)、F線(青■)の３色だけを考えます。(カラーバランスを考えると、C線(赤)、e線(緑)、F線(青)のような気もしますが。) 　ニュートンは、ガラスでプリズムを作成すると色が虹色に分離してしまうことを発見し、その現象について研究しました。その結果、「どのようなガラスでも色が分離してしまうことは、ガラスの宿命であり、色が分離しないガラスは存在しない」つまり、「色収差は、ガラスレンズを使う限り決して除去できない」と結論しました。

色収差の除去は本当に不可能なのか？

ニュートンが「不可能だ」と言い切った色収差の除去。 　賢明なみなさんなら、もう答えは知っているでしょうから、説明の必要もないかもしれませんが、話を進めます。 　もし仮に、屈折率の割り当てが逆、つまり、赤いほど強く屈折するガラスが存在し、しかもズレの大きさを同じにすることができれば....。 　第一レンズでC線とF線の焦点位置が分離してしまうのを、魔法の第二レンズがC線とF線を逆向きに分離させるため、結果的にキャンセルすることができるはずです。 ↓の関係式は嘘ですが、たとえば、 nF1+nF2=nC1+nC2 →２枚のガラスの屈折率の和が、２つ(以上)の色で一致すれば、色ごとに同一の焦点距離にすることができる…とか…。

色消し条件の成立

色ズレが起きないようにしたレンズのことを、色ズレをうち消すという意味で「色消しレンズ」と言います。 　色消しレンズとなる条件は、次の通りです。 　ところで、色消し条件式自体は簡素なんですが、アッベ数νって、なんでこんな変な計算をするのでしょう？ もう少しスマートな表現方法があっても良さそうな気がしません？ 【補足】 　さきほどの屈折率の和による色消し条件の関係式はデタラメです。正式な色消し条件式を考えてみましょう。 　もう一度、各色ごとの焦点距離を求める式を、じっくりながめてみましょう。おもしろいことに気がつくはずです。 　気がつきました？ ・C線の屈折率 ・F線の屈折率 この２つは、互いに何も関係がありません。互いに独立した数値です。 　ということは、 ・C線の屈折率とC線での焦点距離の関係式 ・F線の屈折率とF線での焦点距離の関係式 この２つの式の間には、何の関係もないのです。 　関係ない式ということは、互いに独立した結果を決めることができる、ということです。 　つまり「焦点の位置を大きく引き離すも一致させるも、原理的には自由自在に可能」と言えるのです。 　色収差をなんとかしたいのですから、「一致させる条件」が欲しい訳です。一般の眼視用レンズの場合、C線とF線の焦点を一致させるような制御を行います。そして、どうなれば一致する条件になるかと言うと……。 　そして、この式から、次の重要な２つのことが言えます。 νという数(アッベ数)が、屈折率だけで構成されるので、ガラス固有の特性を表現できる、大切な定数になる 色消しの条件を満足するには、必ず正と負の焦点距離をもったレンズ(凸レンズと凹レンズ)を組み合わせなければならない 【補足２】 　さて、色消し条件の証明が終わったのですが、ここで、非常に重大な疑惑が発生します。 　なぜ、私みたいな平凡(?)な人間にもあっさり解けてしまう色収差補正条件を、あの偉大なるニュートンが発見できなかったか?です。 　この程度の証明問題ならば、ニュートンほどの頭の持ち主であれば、あっさり解けていたはずです。 　これは、あくまでも推測に過ぎませんが、 (1)ニュートンは、光の粒子論を信じていた(光の本質が解明されていなかった) 　(スネルの法則は、波動論からでないと導けません) (2)ガラスの種類が乏しく、屈折の関係を詳しく考察できなかった 　(当時存在したガラスは、カットグラス用などの工業用ばかりで、光学ガラスはありませんでした) (3)色ズレが起こる原因や、屈折と色ズレの大きさの関係などについて、掘り下げた研究を怠った 　(ニュートンは、「ダメだこりゃ」と言ったかどうかは知りませんが、屈折式望遠鏡の研究をやめ、反射式望遠鏡を開発したのは、あまりに有名な話です。) などの要因が重なったためでしょう。 　本当の原因はわかりませんが、いずれにせよ、ニュートンが色消しレンズを発見できなかったことが、光学の発展が100年以上も遅れる原因となったのは、事実のようです。 【補足３】 　もちろん、色消しの条件のもう一つに「通常の凸レンズと、赤の方が近くに焦点を結ぶ凸レンズ(νが負のレンズ)を組み合わせる」というのがあります。ただし、残念ながらνが負のレンズは存在しません。 　が、なんと!!　キヤノンが2000年に作ってしまいました。その名も「積層型回折素子」。 　要するに同心円状の回折格子です。回折格子を通った光は、別の角度に光が曲がるものが現れます。ただし、波長が長いほど強く回折するので、プリズムとは逆の色ずれが起きます。 　回折格子を同心円にして、しかも格子のピッチ(格子定数)を中央と周辺で変え、凸レンズのように焦点ができるように工夫したのが、この素子です。 　ただし、円形回折格子をレンズのように使うテクニックは、昔から知られていて、別に大した発明でもなんでもありません。しかし、普通に作ったら、目的の光以外の光(素通りする光もあれば、反対側や、さらに強く回折する高次回折光などなど)が散らばってしまって、レンズのようにきれいな像にならず、使い物にならなかっただけです。 　それを目的の回折光だけを通すようにした所が、キヤノンの「大発明」のポイントのようです。