球面収差の補正のためには、球面収差図が不可欠です。
球面収差図とは、レンズにある高さhで入射した光が、各レンズ面で屈折した結果、光軸とどこで交わるのかを示した図です。
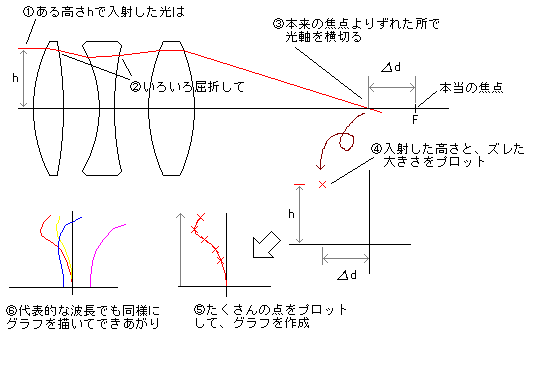
で、ここで問題なのが(2)番。各面を屈折する様子ってどうやって計算するんでしょう?
いろいろな文献を見ても、「スネルの法則 n sin i=n'sin i' の式を直接使って計算します。」しか書いていません。それを「三角追跡」というそうですが、具体的なことについては、全然ふれてません。
仕方ない。やりますか。自力で。
|
色消しレンズができあがり、いよいよ球面収差の補正にとりかかります。 球面収差の補正のためには、球面収差図が不可欠です。 球面収差図とは、レンズにある高さhで入射した光が、各レンズ面で屈折した結果、光軸とどこで交わるのかを示した図です。  で、ここで問題なのが(2)番。各面を屈折する様子ってどうやって計算するんでしょう? いろいろな文献を見ても、「スネルの法則 n sin i=n'sin i' の式を直接使って計算します。」しか書いていません。それを「三角追跡」というそうですが、具体的なことについては、全然ふれてません。 仕方ない。やりますか。自力で。 |
光軸に平行な光が、曲率半径rのレンズのある高さhに当たり、その面でω2だけ曲がっていく様子を考えます。この面の屈折は、簡単です。簡単なので、第二面以降や、斜めに入射する光のことも考えて、「ω1で入射した光が」という条件まで足しておきましょう。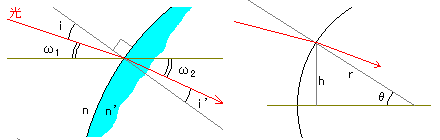 この図から、  はい、終わり。 sin-1(x)とは、sin関数の逆関数で、アークサインと言います。sin関数が角度を与えてやると直角三角形の辺の比率を返すのとは逆に、直角三角形の辺の比率を与えると角度(ただし、ラジアン)を返します。 数学では、逆関数に頼った書き方は禁じ手なのですが、ここは実用本位で逆関数を使いまくります。 アークサインを直接使えるコンピュータ言語は、FORTRANぐらいしかないので、展開式を示します。 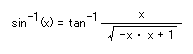 なお、tan-1(x)は、tan関数の逆関数で、アークタンジェントと言います。これは、(COBOLを除く)どのコンピュータ言語にも標準関数として用意されていて、arctan( ) とか atan( ) とか atn( )という名前になっています。この辺はマニュアルを確かめてください。 臨界角を越える(n sin i/ n' >1)と全反射を起こしますが、対物レンズでそういうことは起こり得ない(起こるようなものは実用にならない)ので、無視します。 |
第一面のh1から、(光軸に対して)ωだけ傾いて射出された光は、中心肉厚d1だけ離れた第二面の高さh2の場所に達します。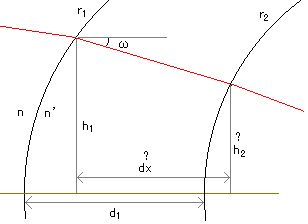 今までは「近軸領域」ということで、手抜きをしてきましたが、球面収差図は手抜きなしで描画しなければなりません。 さて、今回のメインイベント。水平距離dxと、r2の入射高h2をどうすれば計算できるか、という問題です。曲率半径r1とr2は違いますから、d1とdxは等しくありません。光はωだけ角度をもって斜めに進んでいますから、h1とh2も等しくありません。 今回は近軸領域ではないので、面の出っ張り(高い位置での後退)も無視できません。 さて、どうやって求めるのでしょうか。 これは、試験問題でも何でもないので、「ちょっとしたヒントですぐ解ける」保証がなく、たった数行で済むのか、数百行もの式になるのか、皆目見当がつかない問題です。 ま、数百行になることはないでしょうから、地道にやりましょう。 まず、不要な線を消して補助線を加えて整理し、各点に記号を付けます。 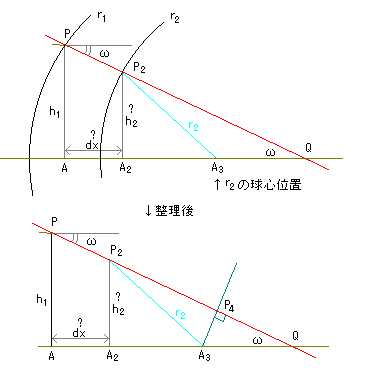 (補助線A3P4を見つけるのに苦労したんだぞ!) 図を別窓で開くには、ここをクリック さて、h2とdxの長さの求める指針ですが、 PAはh1 ですから、わかっています。 △PAQは、1つの角がωの直角三角形ですから、各辺の長さは三角関数を使えばすぐわかります。 長さAA3は、中心肉厚や、r2などがわかっているので、どうにか計算すればわかるでしょう。点Aは、屈折点Pの真下、A3は、面r2の球芯位置です。 となれば、△PAQと△A3P4Qは相似(同じ角を共有する直角三角形)なので、QA3もわかります。 QA3がわかれば、△A3P4Qも直角三角形なので、QP4もわかります。 また、A3P4もわかります。 r2は、わかっていますから、△A3P4P2が直角三角形なので、P2P4もわかります。 P2P4とP4Qがわかったということは、P2Qの長さがわかったということです。 P2Qの長さがわかれば、PQとP2Qの比がわかります。 △PAQと△P2A2Qは相似なので、h2とA2Qの長さがわかります。 A2Qがわかればdxがわかります。 風が吹けば桶屋が儲かります。 あとは、具体的に解くだけです。 まず、「どうにか計算すれば」というAA3ですが、 点Aからの出っ張りx1と、面間隔d1と、r2の曲率半径の和です。 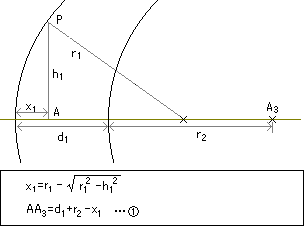 点Aを原点、右に行くほど+、曲率半径はでっぱって+なので、x1は引きます。 前の[図]に戻って、  ということで、各式のA〜Iを順次計算するだけです。中間結果を入れて整理すればいいんでしょうが、数学の問題を解いている訳でナシ、式が簡単になったからといって、計算が楽になる訳でナシ。(計算するのはコンピュータだから。)計算時間が短くなる訳でナシ。(コンマ数秒です。) ま、整理したければ、どうぞ。 さて、これで各面での屈折角と面間隔計算はできるので、入射高hをすこしずつずらしながら、光軸との交点位置を求め、球面収差図を描画します。 球面収差図は、高さ0(限りなくゼロ)のd線の光軸交点を原点にとります。 ただし、h=0は計算できません。(考えれば当たり前のことで、光軸を貫く光は全く屈折しませんから、焦点も結びません。)光軸スレスレの計算は、近軸の計算の方が正確です。 …なんて言ってますが、合ってるのか不明です。誰か検算お願いします。 m(_ _)mぺこり |