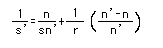近軸領域の計算

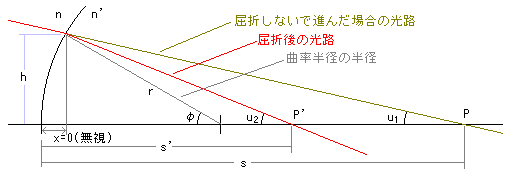
【補足】 　数学的に言って、「sinθ=θ」なんていうことはあり得ません。 　しかし、物理学では「計算が面倒」「どうせ考えても無駄なくらい充分小さい数だから」という理由で、項目を省略したり、都合のいいように解釈を変えたりすることが多くあります。 　F15の望遠鏡の集散角(バージェンスアングル:光軸と光線が交わる角度)は、せいぜい2度ですから、sinθ=θでも小数点以下5桁ぐらいの精度は保てるのです。 　「レンズの厚さがない」ということについても、レンズには必ず厚みがあるので、あり得ません。しかし、手元にあるレンズを実測したところ、2枚合わせて厚さは直径の20%。これをF15の屈折望遠鏡に当てはめて考えると、焦点距離に対するレンズの厚さの割合は、実に1.33%と、わずかです。あながち「省略のしすぎ」でもないのです。 脱線しました。 　sinθを級数展開(*1)すると、次のようになります。ただし、θは、ラジアン(*2) です。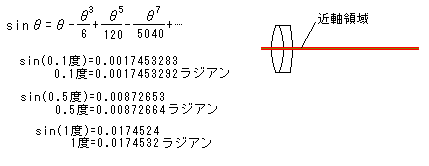 θ(ラジアンの角度)と、sinθを並べてみました。θとsinθは、角度が小さいとだいたい一致してしまいます。 tanθも、角度が非常に小さいと同様に、ほぼθと一致します。 　たとえば、近軸と言うには少し角度が大きいですが、2度=0.034906...ラジアン、sin 2度=0.034899...と、小数点以下５桁程度の精度は保っています。

(*1)数学者のテーラーが考えたことから、テーラー展開とも言われる。今、高校で習うんだろうか？ (*2)ラジアン：角度の単位で、半径と円弧の長さが同じになるときの角度が1ラジアン。180度はπ(3.14159...)ラジアン。

ひとつの球面での屈折

ある光が曲率半径rのレンズ面の、ある高さhで屈折し、屈折しなければPで光軸を横切るはずが、屈折したことでP'に到達した場合を考えます。 このとき、屈折前の焦点位置Pが、屈折することで焦点位置P'になり、屈折しなかった場合の距離sが、屈折後に距離s'となるという関係を、近軸領域では、次のように書くことができます。 「ある高さhで屈折し」と言った割には、hが式の中に入っていません。式の展開途中で消えて無くなるから無いのですが、入射高hを考えなくてもいいほど光軸スレスレの話なので、hは、ほぼゼロと考えてください。 【補足】 1式,2式の解説図を別窓で開くには、ここをクリック 3式の解説図を別窓で開くには、ここをクリック (1)の上の式でu1を求め、(2)式でφを求め、(3)の式を上から順に解いていって、最後に(1)の下の式を使えば、どんな高さhを与えても正確にs'を求めることができます。しかし、このままでは、互いの関係がよくわかりません。そこで、