イーソスは1本10万円前後もする、いわば「究極の接眼レンズ」なのに、どうした事でしょうか?

※ネガティブキャンペーンではありません。
2012/02/12
|
|
|
最近流行の見かけ視界100度を超える、超広角接眼レンズ。テレビューのイーソス13mmは「イーソス13mmの最大角倍率歪曲は視野全体のわずか1%」と謳っているのに、ユーザーレビューを見ると「イーソスは歪曲収差がひどい」とか「ナグラーもイーソスほどではないが、強い糸巻き状歪曲収差がある」いう意見が意外に多いです。 イーソスは1本10万円前後もする、いわば「究極の接眼レンズ」なのに、どうした事でしょうか?  ※ネガティブキャンペーンではありません。 2012/02/12
|
|
歪曲(わいきょく)収差とは、簡単に言うと、タイルの目地を見たとき、タル状または糸巻き状に歪んで見える収差。 類似する収差として湾曲(わんきょく)収差というのがありますが、これはピントの位置が中央部と周辺部で違ってしまう収差。焦点面が球面状になります。 湾曲収差がある場合、視野中心部でピントを合わせると、視野周辺でピンぼけになります。 本題の歪曲収差は像面は中央部と周辺部で倍率が違うという収差です。 視野中央に比べて周辺部の倍率が高いと糸巻き型に、周辺部の倍率が低いと樽型に曲がって見えます。 論より証拠。実際に見てみましょう。  ↑これは、パンオプティック22mm(見かけ視界68度)の実際の画像。それほど欲張った見かけ視界ではありませんが、パンオプティックにも強い歪曲収差があって、ビルの壁面等を見ると、曲がって見えます。  ↑こちらは、某社(というか、忘れた)の17mm(見かけ視界70度)の画像。こちらは歪曲収差がほとんどありません。 2012/02/05
|
|
収差は除去された方が良いに決まっています。 なぜ高級接眼レンズに限ってなぜ素人にもわかるような、盛大な歪曲収差を残すのでしょうか? ――というのが、このページの趣旨です。 いや、テレビューのページで解説してありますけどね。 もう少しわかりやすく。 2012/02/05
|
たとえば、見かけ視界90度とか100度という接眼レンズを想定します。この接眼レンズを今、視野周辺部:光軸に対して45度の方向を見ていると仮定します。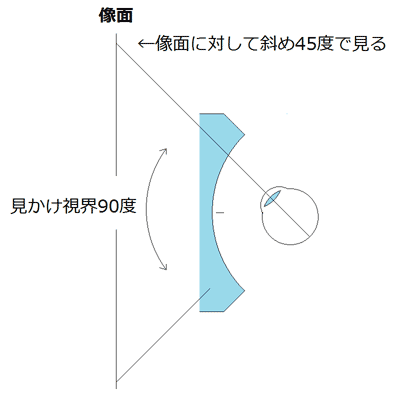 (※この接眼レンズには像面湾曲はありませんので、像面は平面です。) このとき、視軸は像面に対して45度で見る事になります。 いいですね? 次の画像。 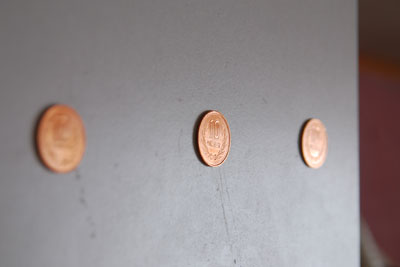 これは、机の端に10円玉を並べて、眺めたときの画像です。 自分の正面にある10円玉ではないので、斜めから見ています。 斜めから見ているので、10円玉は楕円に見えます。 普通ですね、見ての通りですから。 さて。 仮に、収差が完全に除去された(=歪曲収差のない)接眼レンズで木星や土星を見たとします。 歪曲収差が完全に補正された接眼レンズでは、視野周辺ほど像がつぶれてくるんです。 机の端の10円玉の画像のように。 たとえば、テレビを、インチ数の半分弱の距離から見ると、ほぼ90度〜100度の視界で映像を見ることができます。 20インチなら25cmです。50インチなら63cm。ミニシアター級の200インチなら2.5メートル。常にスクリーン中央だけを見ているなら歪みは無いのですが、スクリーン中央とスクリーンの端を見比べると、距離差があまりに大きすぎて、かえって画面中央が出っ張ったように感じます。 2012/02/12
|
|
天体望遠鏡の倍率というのは、角倍率を言います。 仮に、月の実視直径が0.5度のとき、望遠鏡で拡大したら50度に見えたとします。この場合、50度÷0.5度=100倍、となります。 肉眼で見た角度と、拡大したときの見かけの角度の比が倍率です。  ちなみに、顕微鏡の場合は横の倍率と言って、明視距離(25cmの距離)で見た時の大きさに対して何倍に拡大されているか(1mmのものが1cmに拡大されたら10倍)という定義です。 さて。 いきますよ。 パネルに10円玉を3枚貼って、これを遠方に置いたとします。 そして、このパネルを、望遠鏡で見るとします。  見かけ視界100度の超広角の接眼レンズを使い、今、視野いっぱいにパネルが見えているとします。 実際の視野内では、右の10円玉と左の10円玉の見かけ上の角度がほぼ90度です。 どうです? 歪曲収差が補正された接眼レンズでは、上の画像のようには見えません。 両端の10円玉は、まるで机の両端に置いた10円玉のようにつぶれて見えなければならないのです。 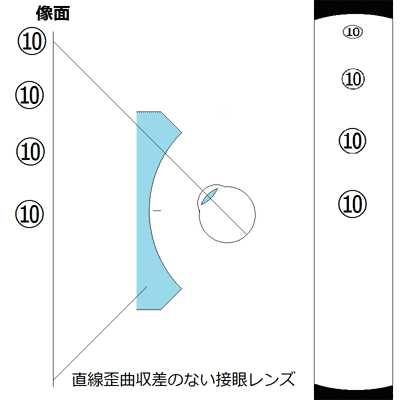 像面は平面で、対物レンズにも収差は無い(という仮定)ので、像面上では像が整然と結像します。これを超広角接眼レンズで90度、100度という範囲に拡大するため、歪曲収差が補正された接眼レンズでは、視野周辺で縦方向と横方向で(サジタル面方向とメリディオナル面方向で)角倍率が変わってしまうという問題が出るのです。 2012/02/12
|
|
超広角の接眼レンズは、実視界も広いため、経緯台で木星などを観測するには便利な接眼レンズです。 視野周辺部に木星を置いてじっくり観察し、スケッチ等をしている間に日周運動で移動していき、また視野周辺に移動させて…を繰り返してスケッチを完成させたりします。 つまり、観測のための接眼レンズは、視野内全体で角倍率が一定である事が求められるのです。(二重星の間隔は、視界のどこにあっても同じでなければならない、というような言い方をしていますが。) 視野を天体が横断している最中に、天体の縦横の比率が変動するようでは観測に使えないからです。  この10円玉のパネルが見かけ視界90度や100度に引き延ばされても、左右の10円玉は自分に対して正面を向くような大きさで見えるべき、という解釈です。 観測のための接眼レンズでは視野周辺で起きる角倍率の不統一を防ぐために、視野周辺に行くほど直線倍率を上げて「角倍率一定」の条件を満たすように「角倍率歪曲補正」します。視野周辺部で横倍率が上がるということは、必然的に糸巻き状歪曲収差が発生してしまいます。 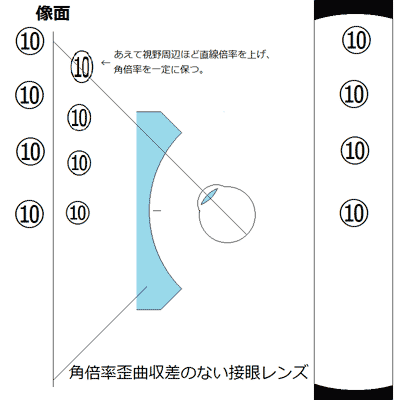 もう一度実際の像で確認してみましょう。  ↑パンオプティック22mm。歪曲収差はあるが角倍率補正されているので、電柱はまっすぐ平行。→視野内で角倍率が一定  ↑某17mm。直線歪曲補正されているので、電柱は視野周辺に向かって放射状に細くなっている。→視野中央部と周辺部で角倍率や縦横の比が変わる 角倍率一定を保ちながら歪曲収差を補正すること=角倍率歪曲収差と、直線歪曲収差の同時補正は物理的に不可能です。 ――というのが、テレビューの言いたいことかと。 2012/02/12
|
|
これは、カメラレンズの超広角レンズに共通する問題です。 一般にカメラの超広角レンズは中心射影方式と言って、レンズを中心に点対称となるような投影を行います。結果的にレンズを中心に点対称で投影されるので、歪曲は発生しません。 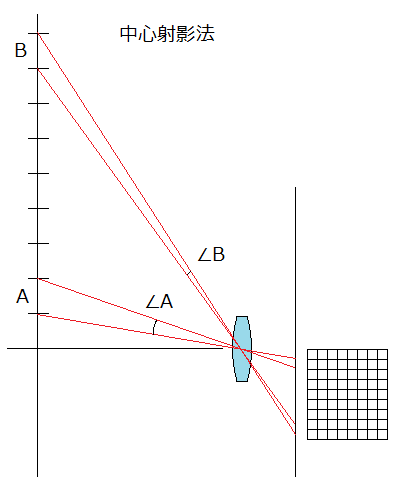 ただし、∠Aと∠Bは、見ての通り「見かけの角度」が異なってしまいます。 レンズを接眼レンズとして見た場合、視野の端ほど小さく見えることを意味します。 これに対して、中心射影方式ではない方式で投影するレンズを「魚眼レンズ」と言います。魚眼レンズにも様々な方式がありますが、等角投影法の場合「同じ角度に見えるものを光軸中心から同じ距離になるように投影する」という方式になります。 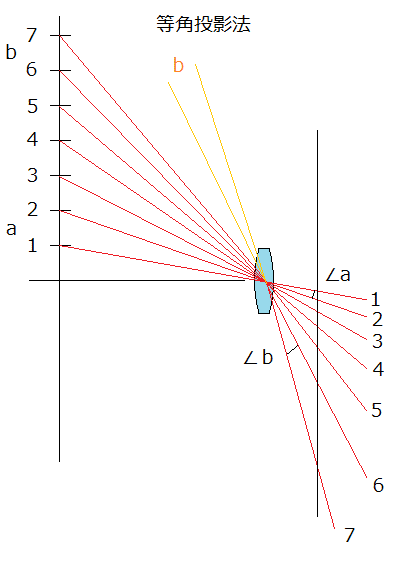 この図の右側を物界(ぶっかい。被写体などがある側)、左側を像界(ぞうかい。フィルムや撮像素子を置いて、結像させる側)とすると、まさに魚眼レンズの投影そのものです。 左から右で見ると、対物レンズが投影した像を接眼レンズで拡大する場合、同じ寸法で並ぶものを同じ角度で投影するので、∠aも∠bも同じ角度で射出されますが、見かけ上のbの位置はオレンジで示したような角度の方向に見える事になります。 直線歪曲収差という意味では、視野の端に行くほど倍率が上がる事になるため、糸巻き状歪曲収差が発生する、となります。 イーソスやナグラーは、言わば「逆魚眼レンズ」という訳です。 2012/02/12
|
|
テレビューの接眼レンズには直線歪曲収差がある事は事実です。 おそらく、今後も補正するつもりはないでしょう。 これを欠点と呼ぶか、仕様として納得するかの問題でしかありません。実際問題、月を視野の端に追いやって見たり、天の川の星々を流す場合を除いて、歪曲が気になる事はありません。 2012/02/12
|
|
[戻る] |