数教協全国高校集会報告　
成田収(札幌啓成高校）　　記念講演は瀬山士郎氏（群馬大）と根上生也氏（横濱国大）との対談でした．数学教育は計算技術の伝承であるとする瀬山さんと，手づくりの数学をみんなで楽しむべきだと主張する根上さん，それぞれの個性が絡み合う印象的な対談だったようです．（真鍋注：瀬山士郎．「数学の目・算数のすがた」日本評論社，根上生也「爽決２１００三話」遊星社，はお勧めの２冊です）　夜は東北の名物先生を紹介するコーナーがあり，個性的な先生が多く登場しました．花巻北高校の宮本次郎先生は数学好きな生徒たちを集めて「少年少女数学愛好会」なるユニークな組織をつくりました．１０年ほど活動を続け，その中から数学科へ進む生徒もでてきているということです．　成田さんは最後に中原克彦さんの「ゲームを利用した組合せ公式の導出」を紹介してくれました．有名な組合せ公式：
　　　　
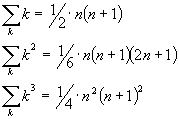
は，次のようなゲームの組合せ総数から導くことができます．例えばＡ，Ｂ，Ｃの３人でゲームをする場合について説明します．各自が１，２，３，…、ｎ＋１までｎ＋１枚のカードを持ち，３人が同時に１枚のカードを出し，大きい数を出した人の勝ちとします．ゲーム全体の組合せ総数は（ｎ＋１)^３です．一方，別の方法でこの組合せ総数を計算することができます．結果は，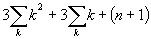　　　　
となります。これから上述の公式を導くことができます。これらは非常に一般性のある内容で、ベルヌーイ数やゼータ関数にも関連しているそうです．そのうちに市民講座の話題としてとりあげられる日を楽しみに，今後の成田さんの研究に期待したいと思います．　

学力低下と今後の数学学習について　
上野健次郎(東京書籍編集部）
 　数学教科書の編集部の方から直接話をきくのは，高校サークルとしても初めての試みです．今回の改訂に関わる高校数学の教科書づくりのなかで，教科書検定官との生々しいやりとりなど貴重な話を間くことができました．　上野さんは，今回の学力低下論争のなかで，文科省は明らかに政策を方向転換したと協調していました．「指導要領は教えるべき内容の上限ではなく下限である」という発言や，教科書会社を集めて「これからは教科書に１０％程度発展的内容を人れてもよい」などと突然言いだしたことにも表 れており，唖然としたそうです．しかし指導要領には「上の学年で習う内容は取り上げてはいけない」や「内容の取扱いを逸脱してはいけない」など多くの縛りがあり，まだまだ自由には書けないそうです．　大学で数学を教えている多くの教員が学力低下を感じており，補講用のテキストに高校の問題集からの転載許可を求めてくる例もあるそうです．　上野さんは，大学生の学力低下は小，中、高と続く日本の数学教育にも間題点があり高校側からももっと実態をアピールすべきだと強調していました．　国大協は学力低下の原因は読解力や論理的思考の不足にあるとしており，この意味でも，数学の学習は大切であると言っていました．笑えない例として，「直線上の点」という意味を文字通り直線の上側に位置する点と勘違いした話なども紹介してくれました．　

折り紙で正多面体をつくる
成田　収（札幌啓成高校）
　２日めの朝は，高校集会で紹介された折り紙による正多面体づくりから始まりました．折り紙は設計図だけではなかなかうまく折れませんが，成田さんの指導でなんとか全員が正三角形と正五角形のユニットを折ることができました．これを使ってオイラーの多面体定理を学ぶプランなども紹介してくれました．　

カヴァリエーリの定理によせて
渡邊　勝（立命館慶祥高校）
　明治図書の「数学教育」‘数学史こぼればなし１１話’の一つとして，カヴァリエーリについて書いてほしい（７月号）と依頼された渡邊さんが，原稿を紹介してくれました．ただし今回は「数学教室」用に書かれた初期原稿の方です．カヴァリエーリについては真鍋が９６年に報告したことがあります．体積に関するカヴァリエーリの原理とは「同じ高さの断面積の比が常にｋであるような２つの立体の体積比はｋである」というものです．彼は不可分量の導入によって後の積分論の先駆けとなりました．　原稿では，三入の鼎談によって４００年前のイタリヤの数学者カヴァリエーリの足跡が歴史に忠実に再現されています．なお渡邊さんは実際に今年の春にイタリヤのボローニャ市を旅行されています．
　
積分の指導について
清水貞人(札幌新川高校）　
　清水さんは留萌工業時代にブリントによる授業「積分とはなんだ」を実践されましたが，今回の報告は新川高校でおこなわれたその再現版というべきものです．積分を区分求積法による面積として定義する方法は，すでに高校サークルでは定番となっています．　プリントでは曲線とｘ軸の間の面積をもとめる問題を中心に理論が展開します．　常に正の値をとる関数ｆ(ｘ）を考え，ｘが０からｘまでのｆ(ｘ）のグラフとｘ軸との間に挟まれた面積をＦ(ｘ）とします．区分求積法から　　　　　Ｆ’(ｘ）＝ｆ(ｘ）という関係が成り立ちます．　いま，例としてｆ(ｘ）＝ｘ^２とすると，Ｆ(ｘ）＝１／３・ｘ^３＋Ｃ（Ｃは積分定数）となりますが，今回議論となったのは面積関数Ｆ(ｘ）に積分定数Ｃをつけるかどうかという問題です．定義から初期条件Ｆ(０)＝０が得られ，積分走数は常に０となるからです．不定積分を使う以上Ｃは必要だとする意見と，最初から定積分
　　　　 
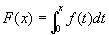
としてＦ（ｘ）を定義すれぱ，積分定数はいらないという意見がだされ，けっきょく結論はでませんでした．　微積分の指導については，プックレットの続編を発行する計画もあり，まだまだ研究を続けていく必要があるようです．
　
７で始まる数
真鍋　和弘(札幌篠路高校）
 　３月例会に報告したものの続編です．この問題が面白いのは，　　　２，４，８，１６，３２，６４，１２８，２５６，５１２，…というよく知られた数列の背後に，思いも寄らない豊かな数学が広がっているからです．なぜ７や９で姶まる数が出てこないのか？という疑問からこの問題を調べていくと，「数の幾何学」と呼ばれる数論の一分野の存在が浮かびあがってきます。これに関わったのはヤコビ，ディリクレ，ミンコフスキー，ワイルといった名だたる数学者たちです．任意の無理数αの分布：　　　　　α，２α，３α，…，ｎα，･･･が円周上で稠密（dence）であることを保証するヤコビの定理，円周上で一様（uniform）であることを保証するワイルの定理などがその成果です．　２０世紀に入り，統計力学と確率論との関係を保証するエルゴード定理に数学者たちの関心が集まりますが，実は，ワイルの定理こそ最初に確かめられたエルゴード定理のうちの一つでした．　その後，現代数学として成長した測度論，確率論，力学系，カオス理論、・・・などがこの問題をモデルとして発展してきたことはよく知られています．　このように，豊かで深みのある数学を高校生や市民に味わってもらえるようになれぱ，数学嫌いも減ってくるのではないかなどと思っています．