�@�@�k�C���n�搔�w���狦�c���@�@�@�@�@�@�@�Q�O�O�T�D�Q�D�P
�@�@��
�Z�T�[�N�������52�@�@�@�@�@�@�@���ӁF������l
�@ |
�u�N�����Ȃ��Ă���l�����ł������悤�v���T�[�N���̌��_�B
�@1��10���ɃT�[�N���a��10���N�̏j�����D�y�s���̃z�e���ōs���܂�
���B�������ψ����̐{�c���F������n�ߑ���15�����W���A��l�ЂƂ肪�v���̏���X�s�[�`���܂����B���Ƃ���̃X�s�[�`�̒��ŁA�T�[�N�����a�����ĊԂ���
�����Ɏ��Ɛ^�炳�k��̐H���Łu�N�����Ȃ��Ă���l�����ł������悤�v�Ƙb���Ă������Ƃ��Љ��A���Z�T�[�N���̌��_��N���Ɏv���o�����Ƃ��ł���
�����B�u�N�����Ȃ��Ă���l�����ł������悤�v�B���̌��t�����ɁA�k�C�����Z�T�[�N���͂��ꂩ����S���e�n���s�r�����������Ǝv���܂��B
�@�j���ɐ旧���A2005�N�x����ƋL�O�u�����s���܂����B����ł́A���
��3���Ɉ���A6���ɖ�ʂŎ��{���邱�Ƃ����F����܂����B�܂��A�������S����͏\���̉��X���ŊJ�Â���܂��̂ŁA�ߗׂ̕��͂��Ђ��Q���������B
�@�L�O�u���ɂ́A�������琔�������ψ����̑������h�����������
���A��N12���Ɍ��\���ꂽ��̍��ۓI�Ȋw�J�����̌��ʂ̕��͂ƁA�����̐��w����̃J���L�������ɂ��Ă��b�������Ă��������܂����B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
| �s2005
�N�x�����v��t |
| �R�� �T�D �U�� |
��� |
���� |
| �U��11�E12�� |
��� |
��� |
| �V��28�E29�� |
�S����� |
�\���E���Ē��w�Z |
| 11��12�E13�� |
�S������ |
�D�y |
| 12��26�E27�� |
�~���� |
�D�y�E�����ڂ̗��� |
�s3�����̂��ē��t
�u�Œ�C���v�Ɓu��̍~������v�̓��{����ւ鈮��ŁA���w�E��
�w����ɂ��Č�荇���A�S���g�ق��ق������C����(�ق��ق���)"�ɂȂ�ЂƂƂ����߂�u����������Ⴂ�܂��B�������A�����������o�E����������
�h�����p�ӂ��Ă��܂��B�����g���A���|�[�g���\��𗬉��`�ق��ق������C����"�𖡂킢�A���w�Ō��C���[�d���ĐV�N�x�̊��J�ɂ������Ǝv���Ă��܂��B��
��ŊF����̂��z�������҂����Ă��܂��B�@�����w���Z�@����m�q
| ���@�� |
3��5��
(�y)�E6��(��) |
|
| ��@�� |
����z�e��
|
����s1��7���ڍ�4��
�@�@�@�@TEL=0166-22-6177
|
| ���@�e |
3
���T(�y) |
14:30��t
15:00���|�[�g���\
18:00�[�H�E�𗬉�
|
|
3
��6(��) |
9:00���|�[�g���\
�P2:00�I���E���U
|
| �Q���� |
1,000�~ |
|
| �h���� |
6,000�~ |
1�����H�t�A�Q����܂� |
| �\���� |
2��17��(��)�܂� |
�ʎ�FAX�ɂ� |
�q�L�O�u���v�|
>
�@��N12���Ɍ��\���ꂽ��̍��ۓI�Ȋw�͒����̌��ʂɂ��āAPISA��
���ʂ��疳����������߂č����X���ɂ���̂ɉ����ē�ɕ������i�s���Ă��邱�ƁAT1MSS�̌��ʂ���V�w�J�ψȗ��̊w�Z�w�J�̕��[�w�������������
�邱�Ƃ����炩�ɂȂ����B�����̒��Œ��ʂ�����ł́A�e�X�g�̂悤�ɔ͌������܂��Ă���킯�ł͂Ȃ��A���ꂱ��̌������o���Ă����悢�킯�ł��Ȃ��B
�����܂������̎�Łu���w�̖��v�Ƃ��Ē莮�����A�����̂��߂̕����E���𗧂ĂȂ���Ȃ�Ȃ��B����ʂɉ����ď_��Ɂu��������v�l���Ă�������
�����̐��w�I�Ȓm���E�Z�\�ƌ��т��Ă����A���̂悤�ȃJ�������Ƃɂ���Ă͂��߂āA���w�̒m���E�Z�\�́u�g����\�́v�ƂȂ�B���߂��Ă���̂́A��
���̕����̒��Ɉʒu�t���Đ��w���w���̌��𑝂₷���Ƃł���B
�@PISA�����ł́u���w�I���e���V�[�v���A�u���w�����E�ʼnʂ�
��������������������\�J�v�A�u�m���Ȑ��w�I���������ƂÂ����f���s���\�J�v�A�u���w�Ɍg���\�́v�ƒ�`���Ă���B����͔[���ł�����̂ł���A����
���u�����Ƃ��Ă̐��w�A���w���ꎩ�̂̊y�����E�ʔ����키�v�A�u�������E���𖾂���w���K�l�x�ƂȂ�w����x�ƂȂ鐔�w�A���w�̗L�p����m��v�̓��
�̑��ʂ���Nj����Ă����B���̂��߂Ɏ��グ��ׂ����w�̗̈�Ƃ��ẮA�u�ʂƐ��E�㐔�v�A�u�ʂ̕ω��Ɗ��E��́v�A�u�Ɛ}�`�v�A�u��ʌ��ہE���R
���̒��̖@���v�A�����ł͂���Ɂw�t���N�^���A�O���t���_�Ȃǁv���܂߂�ł��ł���B���̒�����A�{���ɏd�v�Ȃ��́A���l������́A�w�Ԃɒl������̂���
�Ȃ��i���đI�яo����Ƃ��K�v�ł���B���ɁA�u���w�Z�ŗ��U�I�Ȋ��������v�A�u1�����̒~�ς�2�����ɂȂ邱�Ƃ�m��v�A�u���Z�ł͎w�����Ƃ���
�ω��̓�����m��v���Ƃ͏d�v�ł���B�@(�������h)
��1�����|�[�g�v�|��
�@�@��
���w�Z���w�u����v�̎��ƃv�����@�@�����N�j(�t���k���w����w)
�@�@����́A����̌ŗL�x�N�g���ɂ��Ă̌����B�Ԃ��Ȃ��u�b�N���b�g�Ƃ���
���s�B���ƈđH���Ă��������W���B
�A�@��
��Â�Ȃ�܂܂ɇU�@�@�ۓc���j(���k��w���w�Ȋw��)
�@�@���s���j�b�g(1��������������)����A���e�B���\�z�ւ̃A�v���[
�`���l����B
�B�@���w��`�������c�c�@�@�Γ���(�Ó��_�ƍ��Z)
�@�@�藝�ƑQ�����̎w����ʂ��Č����Ă������k�̂܂����ɂ��Ă̌�
���B
�C�@7�̃t�@���^�W�[�@�@�n粏�(�����ٌc�ˍ��Z)
�@�@���F�u�����E�����O��Ԃ�l�ԏW�c�ƌ����āA���̒��̕����č����T�[�N��
�ł��邱�Ƃ���A���̘A�z�ʼn~���ƌ����Ă��͌^�̏Љ�B
�D�@���w����̃j���[�X�^���_�|�h���m�����čL�߂悤�I�@�@������l(�D�y�V�썂
�Z)
�@�@2���̑S��������c�Ŕ��\������e�B21���I�̎s���ɋ��߂��鐔�w�̋�
�ʋ��{�́A���w�̃��K�l�Ō����̐��E��ǂ݉����\�J�B
�E�@�s
���̐��w��ΐ����W�҂ւ̃X�P�b�`�@�@�@���c��(�Ó����Z)
�@�@�ΐ��̋ߑ�I���߂ƕ��f���ɂ��Ă̍\�z�B������3�����ŁB
�F�@��
�_�I�s�^�S���X�̒藝�@�@�@�^��a�O(�D�y�H���Z�j..
�@�@�\��Ɋւ����j�����ǂ�Ȃ���A�Ȃ��l�X�͐��̕s�v�c�ɑ��ċ����S��
�䂩���̂����Љ�B
�G�@�~
����̎w�����@�ɂ��ā@�@������l(�D�y�V�썂�Z)
���k�̑f�p�ȋ^��u��]����Ɠ���?�v�A�u�C�ӂ̈�l���Œ肷��?�v�ɉ�����
���H�B
�@
�~�@���@��
�@�~�����̑�1�ږڂ͏������̎��H�Ɋw�Ԃ��Ƃ��e�[�}
�ɍs���܂���.����������,���̓~�����ɗ����,���w�Z�̎Z��,���w�Z�̐��w,���Z
�̐��w,��w�̐��w�Ƃ����悤��,���w�ɖ��Ӗ��ȃ��x����\���ċ�ʂ����邱�ƂȂ�,���ׂĂ̐��w�ɂ��čl�����芴�����肷�邱�Ƃ��ł��܂��ꂻ������
�Ӗ��ł͑�ϋM�d�ȏꏊ�ł�.
�@�ŏ��̕�,���{�搶(���撬�����揬�w�Z���{�וF��)�ł��B���{��
���̎����o���}�`�̂������Ⴊ�������낭��,���̂�������̑N�₩�ȐF�ƕs�v�c��
�������ɋ�z���������Ă��܂�.
�@����,�т����������̂�,���s��2�g�̖_��g�ݍ��킹�ĕ��s�l�ӌ`�̌`��
�������������,�����`�������v���X�`�b�N�ł��o�������������
���ׂ�,�q�ǂ��̔F���ł͂��̓�͈قȂ���̂Ȃ�ł�,�Ɣނ��q�ׂ��Ƃ��ł���.���܂őS���C�����܂���ł��������̓��,��l�ɂƂ��Ă�,�q�ǂ�
�ɂƂ��Ă��S���قȂ���̂�,�~�Ƃ������t��,�~��(circ1e)��\���Ƃ���,�~��(disk)��\���Ƃ�������悤��,�O�p�`��l�p�`�Ȃǂ̑��p�`
�ɉ����Ă�,�`������鋫�E�Ɉӎ����W������ꍇ��,���E�Ŏd��ꂽ�̈�Ɉӎ����W������ꍇ�Ƃł͔F�����Ă�����̂��Ⴄ,�Ƃ������R�̂��Ƃ��ĔF��
������ꂽ�悤�ȋC�����܂�.
�@�܂�,�C�ӂ̎l�p�`���P��̌`�̌J��Ԃ���,���ʂ�~���l��
��l�q���J���[�̃v���o����,��ڂŗ����ł���悤�ɂ��Ă��ꂽ��,�C�ӂ̓ʌ^�l
�p�`�͊ȒP��4�̕����ɐ藣����,���בւ���ƕ��s�l�ӌ`�ɂ��邱�Ƃ��ł��邱�ƂȂ�,�y�����ĕs�v�c�ȂȐ��E���W�J����Ă��܂���.����Ȗ��̂���
�Z���̎��Ԃ��W�J����鏬�w�Z�ɒʂ��Ă݂��������ȂƊ����܂���.
�@���w�Z�́̕A�u�V�ċ��t�̔Y�݂ƍH�v�v�Ƒ肵��,����2�N
�ڂ̏��O�}�搶(���X��)�����w���̃e�[�}�Řb����܂���.
�@2�����̓����ɂ�,�ꌩ�W�Ȃ������Ɍ�����u���b�N�{�b�N�X���H�v����
���,���@�\����������Ƃ��̃C���[�W���������,��ӂ��
����2�N�Ԃ̎��H�����Ă���܂���.�V�N�ł݂��݂�����,���C�����ς��̕��Ȃ���.�����̋����ɂȂ肽�Ă̍����v������,��������̌��Ăɗ�
���������G�l���M�[���킯�Ă�������悤�ȋC�����܂�.
�@�Ƃ����.���Ƃł悭�l���Ă݂��,�@���������@�̃O���t��,���ʁ@���{��
���P�@�ȂǂŐ����,�@�������i�P�|���j�@�ƂȂ�̂�,����
��,�W�Ȃ������ǂ��납����2�����̃O���t���̂��̂��ƌ������Ă����̂��ƋC����,�搶�̊����̉s���Ɍh�����܂���
.
�@����ɂ��Ă�,���ȏ��̍���,��X�G���̗Ⴊ����,���
�ώG�ł�.����T�^�ʂ̉�͂ɂ��ʂ�����T�O�𒊏o���悤�Ƃ����p��������
��Ȃ�.����ł͒u������ɂ���鐶�k����������łĂ����������Ȃ��Ǝv���钆�g�ł���̂ɋ�������܂���.
�@���Z��,�����搶(�t���k���w����w�����N�j��)�̍��Z��
�w�u����v�̎��ƃv�����̏Љ�ł�.���̃v������,�������(��`�悪���R��
�ł����)�ƍl��,���ł���ȏ�͉�͓I�ȗ��ꂩ�痝�����ׂ����̂ł��邩��,���̕ω��ɒ��ڂ��邽�߂�,�א�2���Ԃ̍����ɒ��ڂ��ĉ�͂�i��
��ׂ����Ƃ�������ō��ꂽ���̂ł�.�啔�̍�i�ł�����,�����1���ڂɐ���̓����ƌ����`�F�X�Ղ�L���^�s�[�X�ɂ��~���l�ߖ��ɂ�鐔�w�I�A�[
�@�̏Љ�,2���ڂ̒����������ȉ�ɂ�����,�n�m�C�̓��̎萔�̑Q�����ɂ�����,�ŗL�x�N�g���̖����ɂ��Ęb����܂���.����̓����ł�,�K����������
���낢����,
�@�@�@19,58,29,88,44,22,l1,34,�P�V,
52,26,i3,40,20,10,5
�Ƃ���,�R���b�c�\�z(�p�J�\�z)�Ɏ�ނ�������Ȃǂ������Ă��܂�.
�@���w�I�A�[�@�̏Љ��,���̂悤�ȕ��@�ōs���܂�.
��ӂ�2�Q�̌����`�F�X��
 ���@
���@ ��
�~���l�߂���@����������,
��
�~���l�߂���@����������,
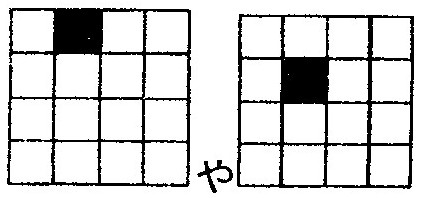 ��
�� �ŕ~���l�߂邱�Ƃ��ł�,���ꂪ�킩���,����
�ǂ�Ȃɑ傫�����ł�,��ӂ�2���ł���`�F�X�Ղ���,�C�ӂ�1���惊�����������`�F�X��
.
�ŕ~���l�߂邱�Ƃ��ł�,���ꂪ�킩���,����
�ǂ�Ȃɑ傫�����ł�,��ӂ�2���ł���`�F�X�Ղ���,�C�ӂ�1���惊�����������`�F�X��
.
 ��
�� �ŕ~���l�߂��邱�Ƃ��킩��܂�.���̋��ނ�
�ʂ���,���w�I�A�[�@�̋��͂ȏ���������邱�Ƃ��ł��܂�.
�ŕ~���l�߂��邱�Ƃ��킩��܂�.���̋��ނ�
�ʂ���,���w�I�A�[�@�̋��͂ȏ���������邱�Ƃ��ł��܂�.
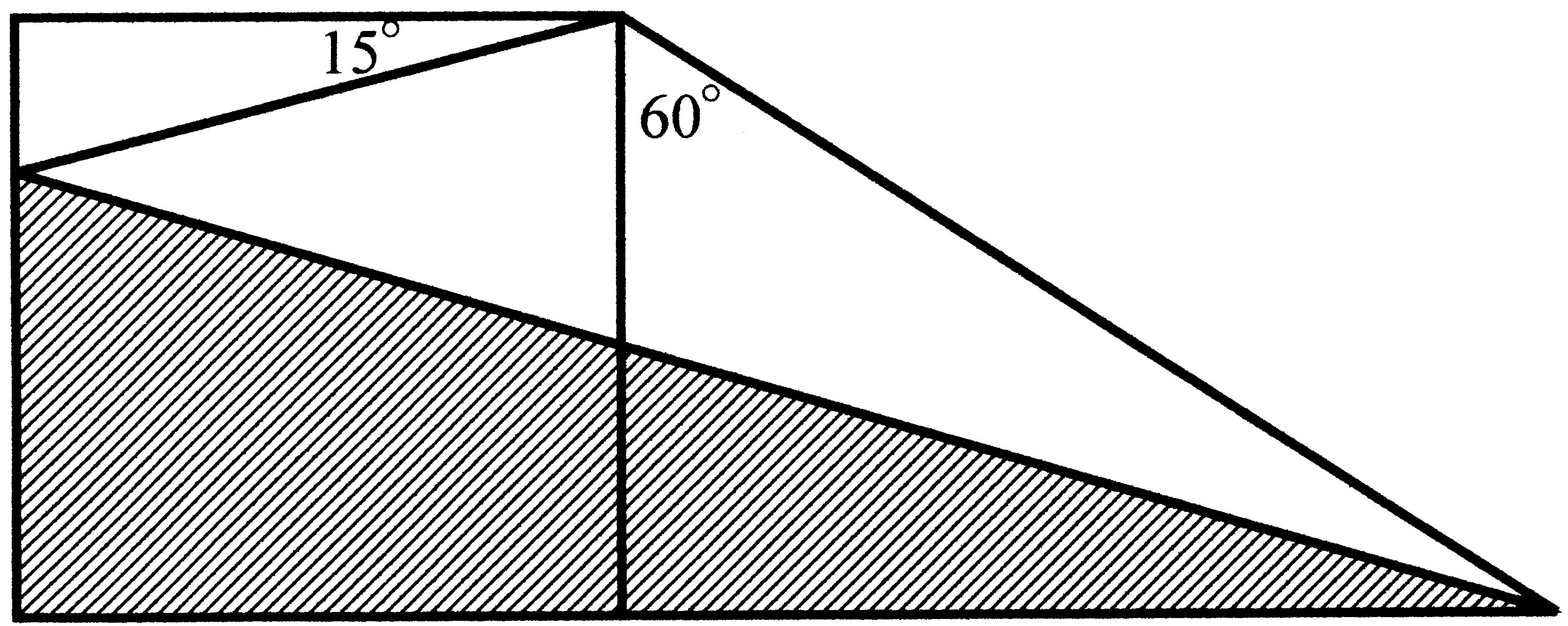
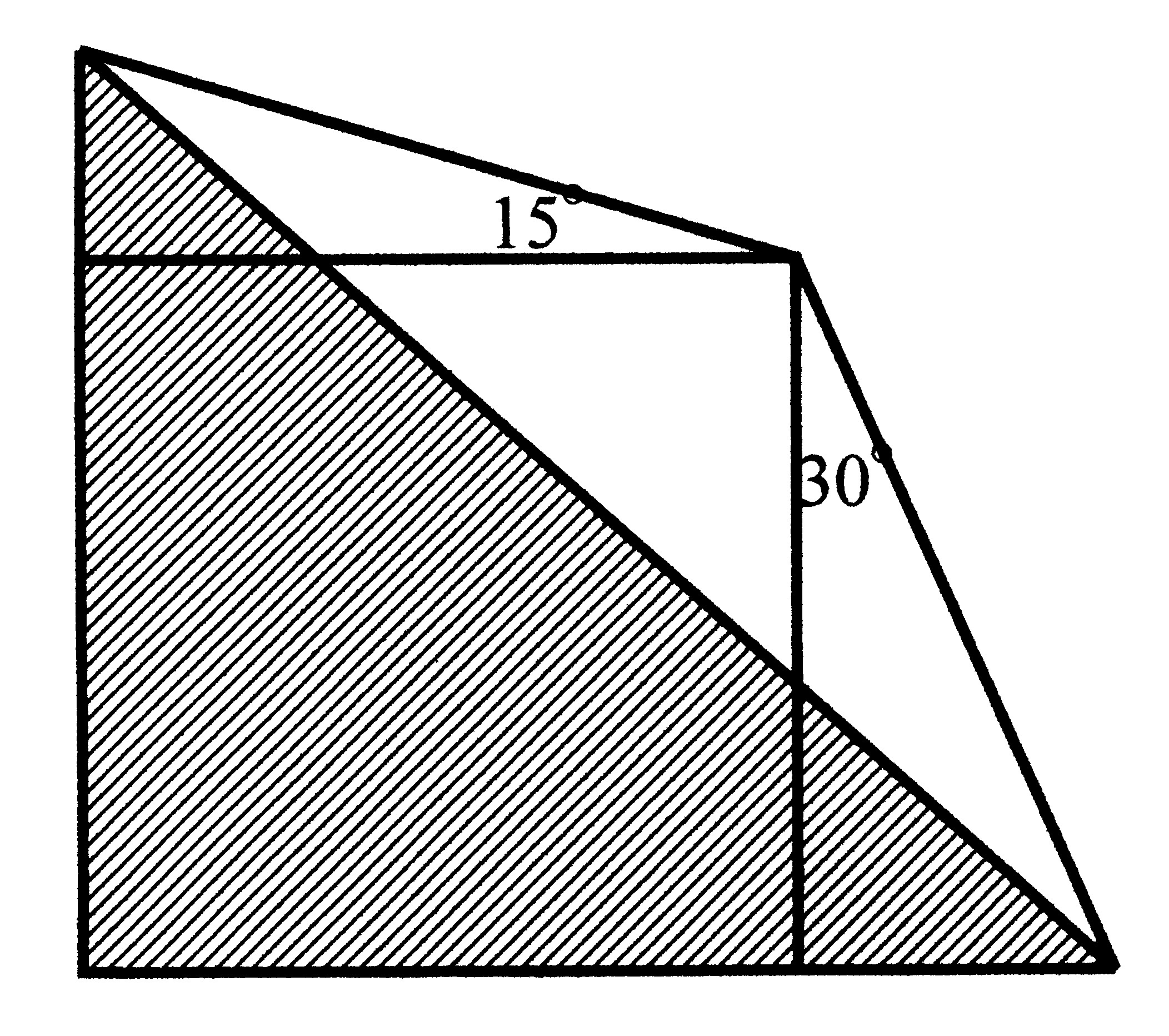
�@����搶(�\���Ǔ��W�X���w�Z����F��)��,1�ӂ�1�̐���
�`�Ɛ��O�p�`����ł���}�`�ɐ}�̂悤�ɐ��������Ăł���}�`�̖ʐς�1�ł��邱
�Ƃɂ��čl�@���Ă��܂��A
�̓h��Ղ��������̖ʊn���}�̒��Ɍ����鐳���`�̖ʐςɂЂ�
�������Ƃ�,��ʂɂ̓h��Ղ��������̖ʐς��}���̐����`�̖ʐςɓ��������Ƃ͓����ł�.
���̖ʐόv�Z�������w�I�ɍs���ƌ����ĊȒP�ł͂���܂���.������
���Ƃ���͂��čs����,�P�T����
�R�O���̊W��,�����ĂS�T���ł��邱�Ƃ��{���I��,��ʂɁ@�����@�Ɓ@����
�@�����{�@�������S�T���̂Ƃ��ɂ����邱�Ƃ��킩��܂�.�����,���̂�
��
��,������ɒ��ڂ����B�����w�I�Ȉ�ڂł킩��w�炵���ؖ������邱�Ƃ�������<��܂���.�y�����ЂƂƂ��ł���.
�@�^��搶(�D�y�H���Z�^��a�O��)��,�u���_�I�s�^�S��
�X�̒藝�v�Ƃ���,�u���Q�{���Q�����Q�@���݂����������������ɑ��݂���v�Ƃ�����
�����������̒藝�ɂ����鐮��z���\�������f���͂��ׂā@4���{1�@�^�̑f���@�ł��邱�Ƃɂ��ďq�ׂĂ��܂�.�����,�@4���{1�@�^�̑f���@���@
�́@�������Q�{���Q�@��,������ʂ�ɐ����̕����a�ɕ\�����Ƃ��ł���Ƃ��������Ɋ�Â��Ă��邻���ł�.���̒藝��,�t�F���}�[���ؖ��Ȃ����q��,����
��,�I�C���[���ؖ���,��������,�K�E�X��2���`���̋c�_�̌`�ő㐔�I�����_��W�J��,����̐����_�ɂȂ����čs�����̂�̍ŏ��̓����ɂ�����Ƃ�����
�Ƃł�.���̕�,���Ԑ��,�ڍׂ����Ƃ��ł��Ȃ������̂��ɂ��܂�܂��A�Ă̑��̊�b�u������苳���ƕ��s�����T�����Ȃǂ�,��x�������
�b���������̂��Ǝv���܂���,
�@�����̑��ɂ�,�����搶,�����搶,�O�A�搶.���J��
���̕���ϗ`���[�����̂ł�����,�������s���܂����̂ŕ͕ʂ̋@��ɂ�������
�v���܂�.�@(���c�q)


 ���@
���@ ��
�� ��
�� �ŕ~���l�߂邱�Ƃ��ł�,���ꂪ�킩���,����
�ǂ�Ȃɑ傫�����ł�,��ӂ�2���ł���`�F�X�Ղ���,�C�ӂ�1���惊�����������`�F�X��
�ŕ~���l�߂邱�Ƃ��ł�,���ꂪ�킩���,����
�ǂ�Ȃɑ傫�����ł�,��ӂ�2���ł���`�F�X�Ղ���,�C�ӂ�1���惊�����������`�F�X�� ��
�� �ŕ~���l�߂��邱�Ƃ��킩��܂�.���̋��ނ�
�ʂ���,���w�I�A�[�@�̋��͂ȏ���������邱�Ƃ��ł��܂�.
�ŕ~���l�߂��邱�Ƃ��킩��܂�.���̋��ނ�
�ʂ���,���w�I�A�[�@�̋��͂ȏ���������邱�Ƃ��ł��܂�.