転がるタイヤの謎
真鍋和弘（札幌篠路高校）
冬になると北海道では道路が凍結してスリップし，毎年多くの犠牲者がでています。冬道で車を運転するときに，自分の車のタイヤが滑っているのか，それとも転がっているのかを判断できることは重要なことなのです。「滑る」と「転がる」の違いを数学で表現することは結構むずかしいのです。タイヤが「転がる」とはどういうことかを理解してもらうために，次の問題を考えてみてください。
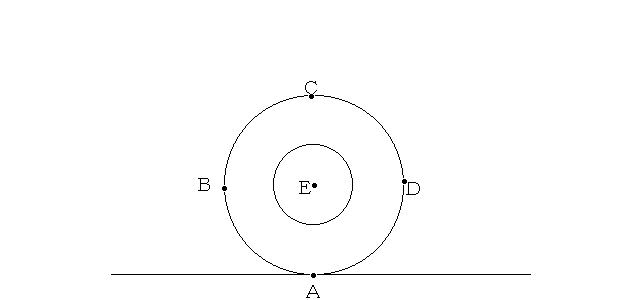
【解答】Ａ点
なぜそうなるのか疑問に思う人もいるでしょう。ここでの主題は「転がる」ということを数学的に表現してみることです。そのためには３角関数と微分についての知識を少々必要とします。転がるタイヤの円周上の１点が描く図形はサイクロイド曲線と呼ばれ，その性質は昔からよく知られています。
サイクロイド曲線
いま半径がａの円板がｘ軸上を図のように回転しながら転がっているとします。円周上の１点Ｐの座標を（ｘ，ｙ）とし，Ｐが描く軌跡を考えてみましょう。図のようにＰの出発点を原点０にとり，円板が角θだけ回転して，ｘ軸に点Ａで接しているとします。この時のＰの位置をもとめてみます。円板が完全に転がるという条件は，孤ＡＰが線分ＡＯにべったりと重なることですから，弧ＡＰと線分ＡＯの長さを等しいとおくことができます。θを孤慶法（ラジアン）で測れば孤ＡＰの長さはａθとなるので，座標（ｘ，ｙ）は
ｘ＝ａθ−ａ
sinθ＝ａ（θ−sinθ）
ｙ＝ａ−ａ
cosθ＝ａ（１−cosθ）
と表されることがわかります。ｘ，ｙをθの関数と考えると平面内の集合
｛（ｘ，ｙ）│ｘ＝ｘ（θ），ｙ＝ｙ（θ），−∞＜θ＜＋∞｝
ば曲線を表します。これをサイクロイド（ｃｙｃｌｏｉｄ）と呼んでいます。もしＰが円板の内部の点であれば（半径ｂの円周上とする），Ｐの軌跡ほ，
ｘ＝ａθ−ｂ
sinθ
ｙ＝ａ−ｂ
cosθ （ｂ＜ａ）
となります。これはトロコイド（ｔｒｏｃｈｏｉｄ）と呼ばれています。
一般に上のような表式を曲線のパラメーター表示と呼びθをパラメーター（助変致）といいます。サイクロイドやトロコイドはθについて何回でも微分可能な（なめらかな）曲線です。
さて．θが時間 ｔ とともに変化するとすれば，θは ｔ の関数と考えられるので，ｔ をパラメーターにとることもできます。あらためて
ｘ＝ｘ
(θ（ｔ）)，ｙ＝ｙ(θ(ｔ))
とかくことにすると合成関数の微分によって，
ｄｘ／ｄｔ＝ａω（１−
cosθ（ｔ））
ｄｙ／ｄｔ＝ａω
sinθ（ｔ）
となります。ここで，
ω＝ｄθ／ｄｔ
は角速度と呼ばれています。２次元のベクトル（ｄｘ／ｄｔ，ｄｙ／ｄｔ）は点Ｐの瞬間速度を表しています。
転がるタイヤの運動学
時間 ｔ とともに，点Ｐがどのように運動するかを解析してみましょう。まず初期条件として，時刻 ｔ＝０ でθ（０）＝０とします。次に，円板が１回転して再び点Ｐがｘ軸に接するときの時刻を ｔ＝Ｔ とします。すなわちθ（Ｔ）＝２πです。
Ｔ は周期と呼ぱれています。ｔ＝Ｔ のときの点Ｐの速度は，
ｄｘ／ｄｔ＝０， ｄｙ／ｄｔ＝０
ですから，タイヤと地面の接点では速度ベクトルは（０，０）となります。つまりこのとき点Ｐは止まっているのです！
速度ベクトルは周期Ｔの周期関数ですから，点Ｐが接地するたびに点Ｐは瞬間的に止まることになります。これで最初の問題の答が点Ａであるこどが証明されました。
速度ベクトルの大きさ，すなわち速さｖは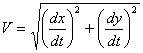 
であたえられるので
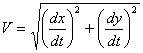であたえられるので 
となります。上の式から，θ＝２ｎπ のときｖは最小値 ０ をとり，θ＝
(２ｎπ＋１)π;のとき ｖ は最大値２ａω をとることがわかります（ただし、ｎ＝０，ｌ，２，３．・・・）。したがって次の定理を得たことになります。
【定理】
半径ａのタイヤ（円板）が完全に転がっているとき，タイヤの円周上のＩ点Ｐの軌跡はサイクロイドである。点Ｐの速さは地両に接するときに最小値０をとり，最上部にきたときに最大値２ａω;をとる。
ガリレイの根対性原理
この定理の定性的な説明を試みることにしましょう。そのためにガリレイの相対性原理と呼ばれる物理学の原理を使うことにします。アインシュタインの特殊相対論はガリレイの相対性原理を拡張したものです。ガリレイの相対性原理とは「あらゆる力学法則はどのような等速直線運動している人から見ても同等に記述される」という原埋です。つまり運動を解析するとき，数式ができるだけ簡潔になるような等速直線運動する座標系（慣性座標系と呼ばれまず）を選んでかまわないということです。
議論を簡単にするために円板の回転を一定にします。すなわち，ω＝ｄθ／ｄｔ は定数です。初期条件を考えて積分すると，
θ（ｔ）＝ωｔ を得ます（ω＞０）。
次に，運動を記述する座標系をこれまでの静止系から，円板と同じ速度で移動する座標系に変換します。円板の中心が移動する速度Ｖは，周期Ｔ（Ｔ＝２π／ω）の間に２πａだけ進むので
Ｖ＝２πａ／Ｔ＝ａω
となります。したがって，ｘ軸方向に遠度 Ｖ＝ａω で移動する慣性座標系から見ると，円板は止まって見えるはずです。このことを具体的に示してみます。新しい慣性座標系からみた点Ｐの座標を（ξ，η）とすると，もとの座標系（ｘ，ｙ）との関係は，
ξ＝ｘ一Ｖｔ
η＝ｙ
で与えられます。力学ではこれをガリレイ変換と呼んでいます。これをサイクロイドの表式に代入すると，
ξ＝−ａ
sinｔ
η＝ａ（ｌ−
cosωｔ）
となります。ここで関係式θ＝ωｔ，Ｖ＝ａ のを使いました。
（ξ，η）の軌跡は図のように中心（０，ａ）で半径ａの円を表すことがわかります。つまり新しい慣性座標系から見ると円板の中心は静止し，点Ｐは等速回転運動だけをするように見えるのです。このようにサイクロイド曲線は
等速直線運動十等速回転運動
という合成によって作ることができます。したがって定理の意味ば次のようにも説明できます。つまりタイヤと一緒に運動している観測者から見ると，円周上の点Ｐが地面に接する瞬間の回転の速度−ａω（ｘ軸方向）と，地面がタイヤに対して相対的に動く速度一Ｖ（ｘ軸方向）とが一致し，この瞬間に点Ｐは地面に対して静止することになるのです。
ガリレイのパラドックス
イタリアの物理学者ガリレイは「新科学対話」という本の中で次のようなパラドックス（逆理）を考えています。
【ガリレイのパラドックス】
外側の半径ａ，内側の半径ｂの円板が図のように転がりながら進んでいる（ｂくａ）。当然，外側の円板が１回転する間に，内側の円板も１回転することになる。
さて，図のように内側の円板が常に接するようにレールをとりつける。さて，外側の円板が１回転すると円板は地面の上を円周に等しい距離２πａだけ進む。同時間に内側の円板もレール上を距離２πａだけ進むことになる（２つの円板はくっついている）。したがって大きな円板も小さな円板も，１同転して進む距離はみな等しくなってしまう。これは矛盾である。
これが正しいとすると，同心円の円周の長さはみな等しくなってしまいます。これはどこかが間違っているはずです。それを調べるために，内側の円板の円周上の点Ｑの運動を調べてみましょう。点Ｑの軌跡は前に解析したようにトロコイドという曲線です。
ｘ＝ａωｔ−ｂ
sinωｔ
ｙ＝ａ−ｂ
cosωｔ
これを時間ｔで微分すると，
ｄｘ／ｄｔ＝ω
(ａ−ｂcosωｔ)
ｄｙ／ｄｔ＝ωｂ
sinωｔ
となります。したがって点Ｑの速さｖ（ｔ）は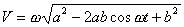 
です。 cosωｔ≦１，ａ＞ｂより，
ａ２
−２ａｂcosωｔ＋ｂ２≧ａ２−２ａｂ＋ｂ ２≧(ａ−ｂ)２＞０
ですから，すべての時刻ｔに対してｖ(ｔ)＞０がいえます。つまりトロコイド上の点Ｑば決して止まることはありません。
定理から，内側の円板が「転がる」とは点Ｑがレール上に来たときｖ
(ｔ)＝０となることですから，内側の円板はレールの上を「滑って」いることになります。ガリレイのパラドックスはこれで完全に解けたことになります。
【参考図書】
［ｌ］長尾汎他「改訂版高等学校数学�」数研出版（１９９９）
［２］アインシュタイン「相対性理論」岩波文庫（１９８８）
［３］ガリレイ「新科学対話」岩波文庫（１９３７）