シェパードの補題

●効用（利益）水準
●支出変化（費用関数の微係数）
●需要量

シェパードの補題

　効用（利益）水準を一定にした場合、第ｉ財の価格ｗｉのみが上昇すると、必要な支出変化（費用関数の微係数）は、第ｉ財の需要量ｘｉに等しい。別な考え方をすれば、消費者が所得ｙ、価格ｗの下での効用において、価格ｗｉのみが上昇した時の効用変化を相殺する所得変化はｘｉに等しいと解釈される。これが「シェパードの補題」の経済学的な意味とされる。

　企業において、生産のための費用関数は産出量の関数であり、生産要素の価格の関数でもある。また、利潤関数は生産物や生産要素の価格の関数である。いま、企業がｙ単位の産出物を生産する場合の要素需要を考えると、投入物たる要素需要は産出水準ｙに依存する。要素価格ｗとして、要素ｉに対する企業の産出水準ｙに依存した要素需要をｘｉ（ｗ，ｙ）とする。この時、費用Ｃが（ｗ，ｙ）において微分可能であり、ｗ＞＞０であれば、次の関係が成立する。

　　　　　　ｘｉ（ｗ，ｙ）＝∂Ｃ（ｗ，ｙ）／∂ｗｉ　　ｉ＝１，･･　，ｎ

これが「シェパードの補題」と呼ばれる命題の数学的な性質である 。この命題の示す意味は、企業が費用最小点で操業している場合、要素１の価格ｗ１が変化すれば、第１要素への支出が増えるという直接効果がある。また、要素の組合せを変えさせるという間接効果が生じる。しかし、費用最小点で操業しているので、このような変化によって利益は生まれないという命題が成立する。

　（証明）
いま、要素価格ｗ* の下で生産量ｙを産出するために、費用最小の要素需要ｘ* が存在すると、

　　　　　　　　　　ｇ（ｗ）＝Ｃ（ｗ，ｙ）−ｗ・ｘ*

なる関数が考えられる。この場合、費用関数Ｃ（ｗ，ｙ）は生産量ｙを産出するための最小費用であり、ｗ＝ｗ* のときにｇ（ｗ* ）＝０となる。つまり、ｇ（ｗ* ）＝０のときがｇ（ｗ）の最大値であり、この点で導関数は必ず０になる。すなわち、

　　　　　∂ｇ（ｗ* ）／∂ｗｉ＝∂Ｃ（ｗ* ，ｙ）／∂ｗｉ−ｘ*ｉ＝０

が成立する。したがって、費用最小にする要素需要は、費用関数の価格に関する導関数によって与えられ、

　　　　　　ｘｉ（ｗ，ｙ）＝∂Ｃ（ｗ，ｙ）／∂ｗｉ　　ｉ＝１，･･　，ｎ

が成立する。

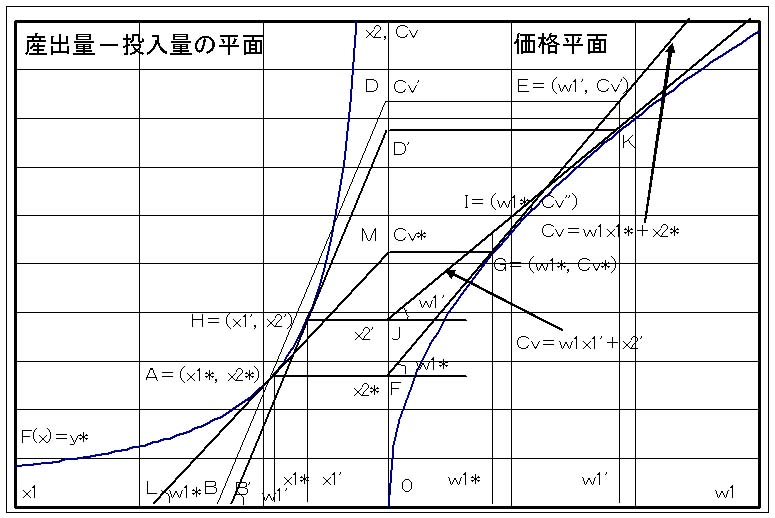
　いま、可変生産要素が２種類の場合を考え、図−１の左側は産出量と投入量の平面であり、第１生産要素の投入量（要素需要）ｘ1を原点から横軸の左向きに取り、第２生産要素の投入量ｘ2を縦軸に取ることにする 。すなわち、与えられた産出量ｙ*を生産するために、生産要素ｘ1とｘ2の関数ｙ*＝ｆ（ｘ1，ｘ2）が存在し、ｘ2＝ｈ（ｙ，ｘ1）なる関係が存在する。単純化のために、第２生産要素の要素価格ｗ2＝１とすれば、第１生産要素の要素価格ｗ1が与えられると、生産に必要な可変費用総額Ｃvは、

　　　　　　　　　　　　　　Ｃv＝ｗ1･ｘ1＋１･ｘ2

となる。また、第１生産要素の要素価格と可変費用総額との関係は、図−１の右側に示しており、横軸に要素価格ｗ1、縦軸に可変費用総額Ｃvを取るものとする。

　さて、関数ｙ*＝ｆ（ｘ1，ｘ1）上にある生産要素ベクトルＡ（ｘ*1，ｘ*2）に着目し、第１生産要素の要素価格ｗ1は、図−１の左側において、直線ＢＡＤの傾きで表すことができる。つまり、直線ＢＡＤはこの時に必要な可変費用総額Ｃv＝ｗ1･ｘ1＋１･ｘ2を示しており、ｘ1＝０の原点において、Ｃv＝ｘ2となり、縦軸との切片Ｄ点が必要な可変費用総額Ｃvとなる。一方、図−１の右側では、要素価格ｗ1の場合、可変費用総額ＣvがＥ点にあり、Ｃv＝ｗ1･ｘ*1＋１･ｘ*2を考えると、直線ＦＥが対応する。これは生産要素ベクトルＡ（ｘ*1，ｘ*2）において、第１生産要素の要素価格ｗ1の変化によって、可変費用総額Ｃvがどのように変化するかを示している。また、直線ＦＥの傾きは第１生産要素の投入量ｘ*1と等しくなる。

　次に、産出量ｙ*＝ｆ（ｘ1，ｘ1）において、第２生産要素の要素価格ｗ2（＝１）が与えられている場合、第１生産要素の要素価格ｗ1における費用最小化問題を考える。この場合、図−１の左側において、可変費用総額Ｃv＝ｗ1･ｘ1＋１･ｘ2は、直線ＢＡＤから直線Ｂ’ＨＤ’へシフトされる。そして、可変費用総額ＣvはＤ点からＤ’点へ低減して、可変費用総額が最小となる。図−１の右側では、要素価格ｗ1の場合、Ｋ点が費用曲線上の最小を表し、費用関数のｗ1についての偏微係数である直線ＪＫ上に存在する。すなわち、直線ＪＫは、要素価格ｗ1における可変費用総額Ｃv＝ｗ1･ｘ1＋１･ｘ2を表し、Ｊ点において要素価格ｗ1＝０となり、Ｃv＝ｘ2が成立する。さらに、直線ＪＫは傾きｘ1を持つことになる。また、図−１の左側のＡ点での接線を考えると、第１生産要素の要素価格ｗ*1は直線ＬＡＭの傾きとなり、Ｍ点が最小の可変費用総額Ｃ*vとなる。この場合、図−１右側のＧ点が費用曲線上の要素価格ｗ*1における最小の可変費用総額Ｃ*vとなる。図−１の右側に示される費用曲線ＯＧＫは、このようにして、生産要素ｘ1に対する要素価格ｗ1における可変費用総額Ｃvが最小となる費用関数を意味しており、直線ＦＥや直線ＪＫなどの包絡線として与えられる。結局、生産要素ｘ*1に対する要素価格ｗ*1における可変費用総額Ｃvが最小となる点は、費用曲線ＯＧＫ上のＧ点で与えられる。そして、費用曲線ＯＧＫを示す費用関数Ｃvにおいて、要素価格ｗ1についての偏微係数は、直線ＪＫの傾きｘ1に等しくなる。これが「シェパードの補題」の図示上で意味するところである。以上のことは生産要素の産出量と投入量に関する量の平面とその価格の平面に双対性の関係があることを示している。つまり、図−１の左側における生産要素のＡ点での接線が図−１の右側における価格平面のＧ点で示され、価格平面で費用曲線のＧ点での接線が産出量と投入量の平面である図−１の左側における生産要素のＡ点で表される。

　このような双対性の関係を用いれば、消費理論の分析が可能となり、所与の価格と所得の下で極大化された効用の大きさを与える間接効用関数や所与の価格の下で一定の効用を実現する最小の支出を与える支出関数の概念に基づく、双対アプローチと呼ばれる手法として応用される。つまり、「シェパードの補題」を用いた双対アプローチは、消費理論にも生産理論にも適用することができる 。

　所与の価格ｐと貨幣所得Ｍの下で効用Ｕを極大化する需要ｘは、ｘｉ＝ｘｉ（ｐ，Ｍ）で与えられ、マーシャルの需要関数と呼ばれる。また、所与の価格ｐと一定の効用水準Ｕの下で支出Ｅを極小化する需要ｘ*は、ｘ*ｉ＝ｘ*ｉ（ｐ，Ｕ）で与えられ、ヒックスの需要関数と呼ばれる。なお、ヒックスの需要関数は、一定の効用水準Ｕを最小の支出で達成するような財の組合せを与えるが、効用Ｕを一定水準に維持するように貨幣所得Ｍが補償的に変化することから、補償需要関数とも呼ばれる。そして、効用Ｕをマーシャルの需要関数で表示すれば、Ｖ＝Ｕ（ｘ（ｐ，Ｍ））＝Ｖ（ｐ，Ｍ）となり、所与の価格と貨幣所得の下で極大化された効用の大きさを与える間接効用関数Ｖが得られる。さらに、支出Ｅをヒックスの需要関数で表示すれば、Ｅ＝Ｅ（ｐ，Ｕ）なる支出関数が得られ、間接効用関数の逆関数で表示される。この場合、支出関数Ｅは、ｐに関して一次同次であり、∂Ｅ／∂ｐｉ＞０、∂Ｅ／∂Ｕ＞０という性質がある。そして、支出関数をマーシャルの需要関数に代入するとヒックスの需要関数が得られ、間接効用関数をヒックスの需要関数に代入するとマーシャルの需要関数が得られるという関係がある。すなわち、支出関数Ｅ＝Ｅ（ｐ，Ｕ）は価格ｐｉで偏微分すると、∂Ｅ（ｐ，Ｕ）／∂ｐｉ＝ｘ+ｉ（ｐ，Ｕ）となり、ヒックスの需要関数が得られる。これは「シェパードの補題」である。また、間接効用関数Ｖ（ｐ，Ｅ（ｐ，Ｕ））＝Ｕは、価格ｐｉで偏微分すると、支出関数Ｕ＝Ｖが一定であることから、

　　∂Ｖ（ｐ，Ｅ（ｐ，Ｕ））　∂Ｖ（ｐ，Ｅ（ｐ，Ｕ））　∂Ｅ（ｐ，Ｕ）
　　―――――――――――＋――――――――――――・―――――――＝０
　　　　　　∂ｐｉ　　　　　　　　　∂Ｅ　　　　　　　　　∂ｐｉ

となる。そして、「シェパードの補題」から、∂Ｅ（ｐ，Ｕ）／∂ｐｉ＝ｘ*ｉ（ｐ，Ｕ）＝ｘ*ｉ（ｐ，Ｅ（ｐ，Ｕ））を用いて、貨幣所得Ｍ＝Ｅ（ｐ，Ｕ）とすると、

　　　　　∂Ｖ（ｐ，Ｍ）　 ∂Ｖ（ｐ，Ｍ）
　　　　　――――――― ＋ ―――――――・ｘｉ（ｐ，Ｍ）＝０
　　　　　　　∂ｐｉ　　　　 　∂Ｍ

となり、これから、

　　　　　　　　　　　　　　　∂Ｖ（ｐ，Ｍ）　　　∂Ｖ（ｐ，Ｍ）
　　　　　ｘｉ（ｐ，Ｍ）＝− ――――---――　／　―――――――
　　　　　　　　　　　　　　　　　∂ｐｉ　　　　　　　∂Ｍ

を得る。この式は、間接効用関数Ｖ（ｐ，Ｍ）を偏微分することで、マーシャルの需要関数ｘｉ（ｐ，Ｍ）が導出できることを意味し、ロワの恒等式と呼ばれている。なお、ロワの恒等式は、右辺の分母∂Ｖ（ｐ，Ｍ）／∂Ｍが所得の限界効用を意味しており、ｘｉとｐｉを入れ替えると効用極大化の条件となり、双対性があることが示される。

＜シェパードの補題：産出量−投入量の平面＞

（文責：ｙｕｔ）

戻る