 電子運動のモデル化
電子運動のモデル化

●電子運動
●電子運動のモデル化
●電子運動の軌道方程式
電子運動のモデル化
1.電子運動の支配方程式
電子を力学的概念に基づく荷電粒子と考える。この場合、電子の電荷eおよび電子の静止質量m0は、
e=1.60219×10−19 クーロン
m0=9.10955×10−31 kg
である。運動している電子の質量はmは、相対論効果による質量変化があり、
m/m0=1/√{1−(u2/c2)} ・・(1−1)
で与えられる。ここで、uは電子の速度ベクトル、cは光の速度である。なお、真空中での光の速度は、
c=2.997925×108 m/sec
である。
電磁界中での電子の運動方程式は、
d(mu)/dt=−e(E+u×B) ・・(1−2)
で表される。ここで、右辺はローレンツ力と呼ばれ、Eは電界の強さ、Bは磁束密度、d/dtは時間tについての微分である。
式(1−2)は式(1−1)の関係を用いると、
du/dt=−(e/m0)√{1−(u2/c2)}{E+u×B−(u/c2)(u・E)} ・・(1−3)
と表示できる。なお、速度ベクトルuは、位置ベクトルrを用いて、u=dr/dtである。
この時、電界の強さEおよび磁束密度Bは、スカラーポテンシャル(電位)VおよびベクトルポテンシャルA
を用いて、
E=−gradV−∂A/∂t ・・(1−4)
B=rotA ・・(1−5)
で表され、マクスウエルの電磁方程式を満たし、次のポテンシャル方程式に従う。
(ε・μ)(∂2V/∂t2)−∇V=ρ/ε ・・(1−6)
(ε・μ)(∂2A/∂t2)−∇A=μj ・・(1−7)
ここで、∇(ナブラ)は、直交座標系(x,y,z)の場合∇=(∂2/∂x2+∂2/∂y2+∂2/∂z2)、
円筒座標系(r,θ,z)の場合∇={∂2/∂r2+(1/r)(∂/∂r)+(1/r2)(∂2/∂θ2)+∂2/∂z2}であり、
εは誘電率、μは透磁率、ρは電荷密度、jは電流密度ベクトルである。また、電子の持つ相対論的な運動エネルギーは、
mc2−m0c2=eV ・・(1−8)
で与えられる。式(1−8)に式(1−1)を代入し、電子速度uについて整理すると、
u=c√[1−1/{eV/(m0c2)+1}2] ・・(1−9)
を得る。
|
Appendix
運動量p=muとおいて、
dp/dt=−e(E+u×B) ・・(イ)
である。これは、
dp/dt=[m/{1−(u2/c2)}](du/dt) ・・(ロ)
となり、
m(du/dt)=−e{1−(u2/c2)}(E+u×B) ・・(ハ)
を得る。ベクトル公式「u(u×B)=0」を用いると、
m(du/dt)=−e{E+u×B−(u/c2)・u・E} ・・(ニ)
が成立する。式(ハ)において、
q=−e{1−(u2/c2)} ・・(ホ)
とおけば、
m(du/dt)=q(E+u×B) ・・(ヘ)
となる。すなわち、電荷量qは速度ベクトルuが光速cに近づくことで、q→0になる。この概念は、荷電粒子の電子の電荷(=−e)が光速上では、見掛け上(古典的対象として)の電荷量qが0(ゼロ)に近付くことを意味する。
(参考)
dp/dt=d(mu)/dt=m(du/dt)+(dm/dt)u ・・(ト)
ところが、
dm/dt=(dm/du)(du/dt)=(d{m0(1−u2/c2)}−1/2/du)(du/dt)
=m0{(−1/2)(1−u2/c2)−2/3(−2u/c2)}(du/dt)
=(1/c2)m(1−u2/c2)−1u(du/dt)
・・(チ)
式(チ)を式(ト)に代入し、
dp/dt=m(du/dt)+(u2/c2)(1−u2/c2)−1m(du/dt)
=[m/{1−(u2/c2)}](du/dt) ・・(ロ)
を得る。
|
2.相対論効果を考慮しない場合の運動方程式
相対論効果や電子流によって生じる磁界を考慮しない場合、電子は負の電荷を持つ質量m0の粒子とみなすことができ、
静磁界中での電子運動を取り扱うことにする。この場合、運動方程式は、
m0(du/dt)=−e(E+u×B) ・・(2−1)
となる。ここで、u=ds/dt,sは電子の位置ベクトル、uは電子の速度ベクトル、Eは電界、
Bは磁束密度、tは時間である。この各成分を直角座標系(x,y,z)で表示すれば、
d2x/dt2=−η{Ex+Bz(dy/dt)−By(dz/dt)} ・・(2−2a)
d2y/dt2=−η{Ey+Bx(dz/dt)−Bz(dx/dt)} ・・(2−2b)
dz2/dt2=−η{Ez+By(dx/dt)−Bx(dy/dt)} ・・(2−2c)
となる。円筒座標系(r,θ,z)で表示すれば、各速度成分は、
ur=dr/dt , uθ=r(dθ/dt) , uz=dz/dt ・・(2−3)
であり、運動方程式の各成分は、
d2r/dt2−r(dθ/dt)2=−η[Er+uθBz−uzBθ] ・・(2−4a)
(1/r)d(r2dθ/dt)/dt=−η[Eθ+uzBr−urBz] ・・(2−4b)
d2z/dt2=−η[Ez+urBθ−uθBr] ・・(2−4c)
となる。ここで、η=e/m0は電子の比電荷である。また、電子の運動エネルギーは、
(1/2)m0|u|2−eV=0 ・・(2−5)
となる。この結果、定常状態において、電子の速度 u は、スカラーポテンシャル(電位)Vによって一義的に決まり、
u=√(2ηV)=5.931×105√V ・・(2−6)
を得る。図−1に相対論効果と非相対論との電子速度の比較を示す。この場合、電位(電子の加速電圧)が約50kV以上になると、工学的な知見から、相対論効果を無視できなくなると考えられる。
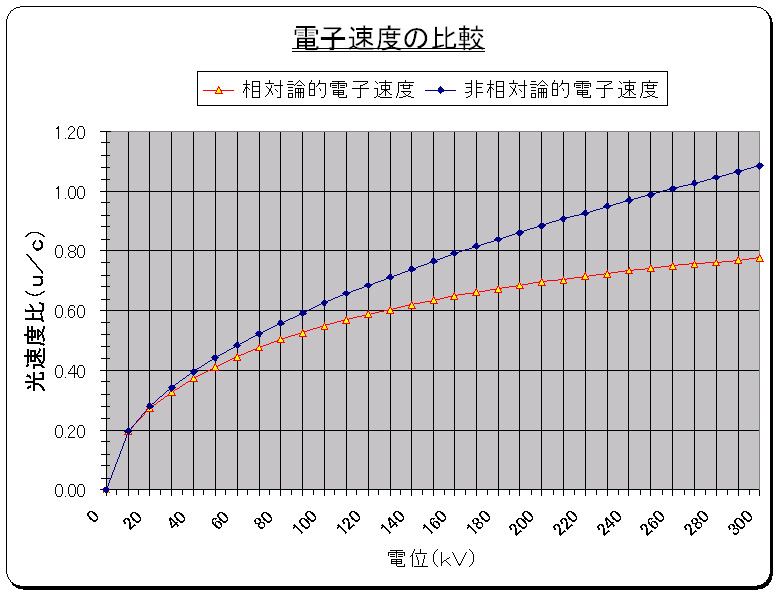
図−1 電子速度の比較(相対論効果と非相対論との比較)
3.電子運動の軸対称軌道方程式
電子運動について、円筒座標系(r,θ,z)から、定常状態(保存系)における軸対称系(r,z)での表示を考える。
この場合、電界の強さ(Er,Eθ,Ez)および磁束密度(Br,Bθ,Bz)は、
スカラーポテンシャル(電位)Vおよびベクトルポテンシャル(Ar,Aθ,Az)を用いると、
Er=−∂V/∂r , Eθ=0 , Ez=−∂V/∂z ・・(3−3)
Br=−(1/r)∂(rAθ)/∂z ・・(3−4a)
Bθ=∂Ar/∂z−∂Az/∂r=0 ・・(3−4b)
Bz=(1/r)∂(rAθ)/∂r ・・(3−4c)
で表される。ここで、ベクトルポテンシャルの回転方向成分Aθについて、ψ=rAθとおくと、
Br=−(1/r)∂ψ/∂z ・・(3−5a)
Bz=(1/r)∂ψ/∂r ・・(3−5c)
となる。したがって、運動方程式の各成分は、
d2r/dt2−r(dθ/dt)2=(e/m0)[∂V/∂r+(dθ/dt)(∂ψ/∂r)] ・・(3−6a)
d(r2dθ/dt)/dt=(e/m0)[(dz/dt)(∂ψ/∂z)+(dr/dt)(∂ψ/∂r)] ・・(3−6b)
d2z/dt2=(e/m0)[∂V/∂z−(dθ/dt)(∂ψ/∂z)] ・・(3−6c)
となる。ここで、式(3−6b)に注目する。微分公式から、
dψ/dt=(∂ψ/∂r)(dr/dt)+(∂ψ/∂z)(dz/dt) ・・(3−7)
であるから、式(3−6b)は、
d(r2dθ/dt)/dt=(e/m0)(dψ/dt) ・・(3−8)
となる。式(3−8)は、時間tについて積分すると、
(r2)(dθ/dt)=(e/m0)∫dψ+C ・・(3−9)
である。これは、t=0の時、r=r0、dθ/dt=(dθ/dt)0、ψ=ψ0とすれば、
dθ/dt=(e/m0){(ψ−ψ0)/r2}+(r0/r)2(dθ/dt)0 ・・(3−10)
となる。式(3−10)は、初速度(dθ/dt)0を考慮したBuschの定理と呼ばれる。Buschの定理は、磁束に巻き付くように円運動する荷電粒子の角速度とその円を通る磁束との関係を表している。いま、電子の出発点である陰極面において、初速度(dθ/dt)0=0 とすれば、
dθ/dt=(e/m0){(ψ−ψ0)/r2} ・・(3−11)
となる。次に、微分公式、
d2r/dt2=(d2r/dz2)(dz/dt)2+(dr/dz)(d2z/dt2) ・・(3−12)
を用いて、式(3−6a)と式(3−6b)を整理する。
(d2r/dz2)(dz/dt)2+(e/m0)(dr/dz){∂V/∂z−(dθ/dt)(∂ψ/∂z)}−r(dθ/dt)2
=(e/m0){∂V/∂r−(dθ/dt)(∂ψ/∂r)} ・・(3−13)
を得る。また、式(2−3)を変形して、
|u|2=2(e/m0)V
(dr/dt)2+r2(dθ/dt)2+(dz/dt)2=2(e/m0)V
(dz/dt)2{(dr/dz)2+1}=2(e/m0)V−r2(dθ/dt)2 ・・(3−14)
を得る。式(3−13)の両辺に{(dr/dz)2+1}を掛けて、式(3−14)を代入すれば、
(d2r/dz2){2(e/m0)V−r2(dθ/dt)2}
+(e/m0)(dr/dz){(dr/dz)2+1}{∂V/∂z−(dθ/dt)(∂ψ/∂z)}
−{(dr/dz)2+1}[r(dθ/dt)2+(e/m0){∂V/∂r−(dθ/dt)(∂ψ/∂r)}]=0
・・(3−15)
となる。さらに、式(3−11)を式(3−15)に代入して、整理すれば、
(d2r/dz2){2V−(e/m0){(ψ−ψ0)/r}2}
+{(dr/dz)3+(dr/dz)}{∂V/∂z−(e/m0){(ψ−ψ0)/r}(1/r)(∂ψ/∂z)}
−{(dr/dz)2+1}[∂V/∂r+(e/m0){(ψ−ψ0)/r}2r
−(e/m0){(ψ−ψ0)/r}(1/r)(∂ψ/∂r)]=0
・・(3−16)
を得る。この式(3−16)は軸対称系(r,z)での厳密な運動方程式である。
4.電子運動の近軸軌道方程式
次に近軸の仮定を示す。
dθ/dt=(e/m0){(ψ−ψ0)/r2}≒(1/2)(e/m0){Bz−Bc(rc2/r2)} ・・(4−1)
V=V(r,z)≒Vz−(1/4)(∂2Vz/∂z2)(r2) ・・(4−2)
∂V/∂r≒(1/2)(∂2Vz/∂z2+ρ/ε)r ・・(4−3)
∂V/∂z≒∂Vz/∂z ・・(4−4)
(1/r)(∂ψ/∂r)≒Bz ・・(4−5)
(1/r)(∂ψ/∂z)≒(1/2)(∂Bz/∂z2)r ・・(4−6)
ρ/ε={1/(πε)}(1/r02){−I0/√(2(e/m0)V0)}
=−(1/2)(e/m0)BB2 ・・(4−7)
を与えると、式(3−16)は、
(d2r/dz2){2Vz−(1/2)(∂2Vz/∂z2)r2−(1/4)(e/m0)(Bz−Bc(rc2/r2)2)r2}
+{(dr/dz)3+(dr/dz)}{∂Vz/∂z−(1/4)(e/m0){(Bz−Bc(rc2/r2)r2(∂Bz/∂z)}
−{(dr/dz)2+1}[(1/2)(∂2Vz/∂z2)−(1/4)(e/m0){BB2−Bz2−Bc2(rc4/r4)}]r
=0 ・・(4−8)
Bc=0の時、
d2r/dz2=[I/{4√2・πε・η1/2・V3/2}](1/r)−{r/(8V)}ηBz2 ・・(4−6)
Bc≠0の時、
d2r/dz2=[I/{4√2・πε・η1/2・V3/2}](1/r)
−{ηB02/(8V)}{(Bc2/B02)(rc4/r4)−(Bz2/B02)}r ・・(4−6)
Ez≠0,Bc≠0の時、
d2r/dz2+(1/2)(1/V)(∂V/∂z)(dr/dz)+(1/4)(1/V)[∂2V/∂z2
−{2/(√(2ηV)}(1/(πε))(1/r2)]r
+{ηB02/(8V)}{(Bc2/B02)(rc4/r4)−(Bz2/B02)}r ・・(4−6)
5.近軸軌道方程式の正規化
次に、電子運動の近軸軌道方程式を正規化する。その条件は、
R=r/r0 , Z=z/r0
α=Bz/BB , β=Vz/V0
K=(Bc/Bz)(rc2/r02)
とする。したがって、
r=r0R , dr/dz=dR/dZ , d2r/dz2=(1/r0)(d2R/dZ2)
Vz=V0β,∂Vz/∂z=(V0/r0)(∂β/∂Z),∂2Vz/∂z2=(V0/r02)(∂2β/∂Z2)
Bz=BBα , ∂Bz/∂z=(BB/r0)(∂α/∂Z) , B0rc2=αKBBr02
を得る。式(4−8)を整理すると、
(d2R/dZ2){2β−(1/2)R2(∂2β/∂Z2)−(1/4)γ{α−(αK/R2)2}R2]
+{(dR/dZ)3+(dR/dZ)}{∂β/∂Z−(1/4)γ{α−(αK/R2)}R2(∂α/∂Z)}
−{(dR/dZ)2+1}[(1/2)(∂2β/∂Z2)−(1/4)γ{1−α2−(α2K2/R4)}R=0
・・(4−9)
が求まる。ここで、γはビーム系のパービアンスPから決まる定数であり、
γ=e/m0r0BB2/V0=(1/(πε))√(2/(e/m0))P
P=I0/V03/2
1/(πε)=4c2×10−7 m2/sec2
である。なお、
近軸軌道方程式を正規化する。ここで、正規化の条件は、
R=r/r0 , Z=174√(P)・(z/r0)
Z={I/(2√2・πε・η1/2・V3/2)}1/2・(z/r0)=174√(P)・(z/r0)
α=B0/BB , K=(rc2/r02)・(Bc/B0)
F(z)=B/B0
r :電子ビーム半径
rc:陰極(カソード)半径
r0:基準点での電子ビーム半径
B0:基準点での軸上磁束密度
BB:半径r0,パービアンスP,加速電圧Vの電子ビームに対するBrillouin値
である。
正規化された電子運動の近軸軌道方程式は、
(d2R/dZ2)−(1/2)[(1/R)+α2R{K2/R4−F(z)2}]=0
F(z)=1+(1/π){tan−1(1/ZA)−ZA/(1+ZA2)} ZA≦0
F(z)=(1/π){tan−1(1/ZA)−ZA/(1+ZA2)} ZA≧0
ZA=z/rA rA:開口半径
である。
(文責:yut)
戻る
| 