|
●周期磁界 周期磁界における電子ビームの安定性
1.まえがき 進行波管などに用いられるPPM(Periodic Permanent Magnet)集束は周期磁界を形成して、磁気レンズ効果による収束作用と電子ビームの発散とを平衡状態にできる。 この時、電子ビームの安定性は一様磁界と比較して劣る。周期磁界中での電子ビームの安定性は、近軸軌道方程式から導出されるMathieu方程式によって、 近似的な検討が可能である。また、周期磁界と一様磁界との対応は磁界の二乗平均値(r・m・s値)を等しくすることによって得られる。 ここでは、周期磁界における電子ビーム系の安定性および電子銃近傍での磁界パターンとの整合について、理論的な検討を行って、 PPM集束を用いた電子ビーム系の設計法に対して適正な指針を与えている。 2.近軸軌道方程式 等電界中での正規化された電子の近軸軌道方程式は、 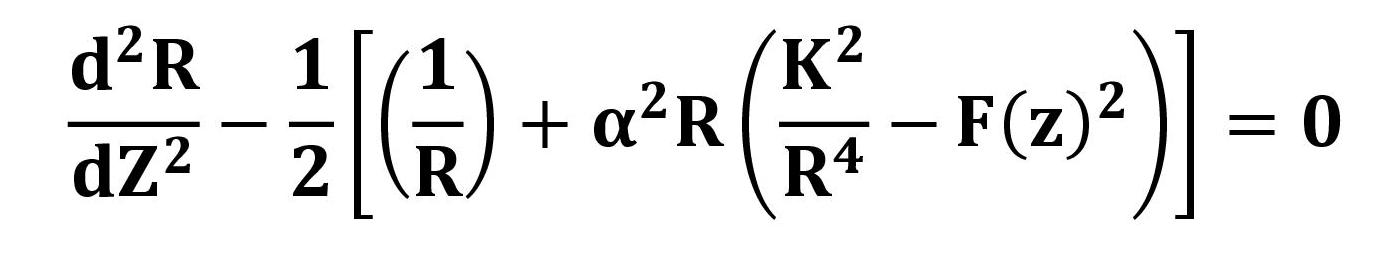 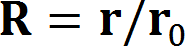 , ,
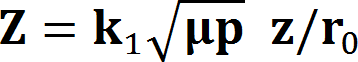 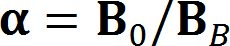 , ,
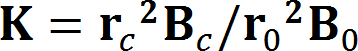 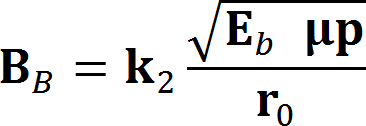 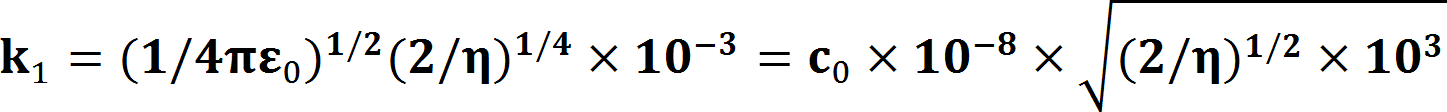 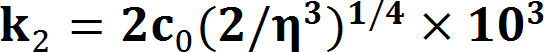   3.磁界パターンのモデル化 軸方向の磁界の強さを正規化関数で表示する。一様磁界の場合はF(z)=1、磁界が存在しない領域ではF(z)=0となる。 また、磁気開口近傍の磁界パターンは、次のようにモデル化される。 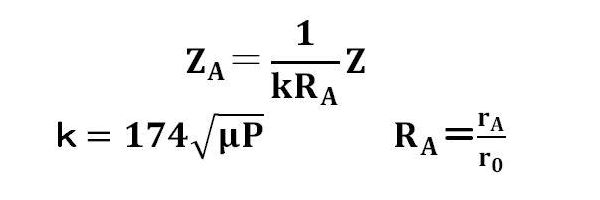 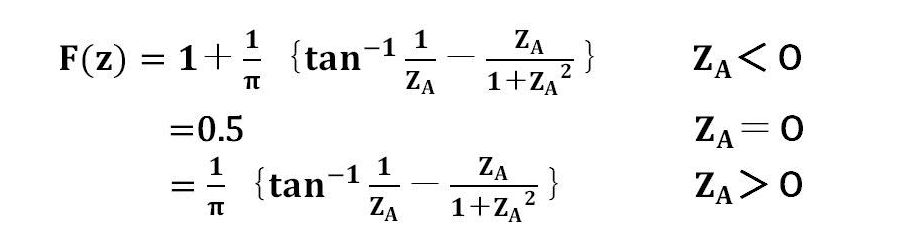 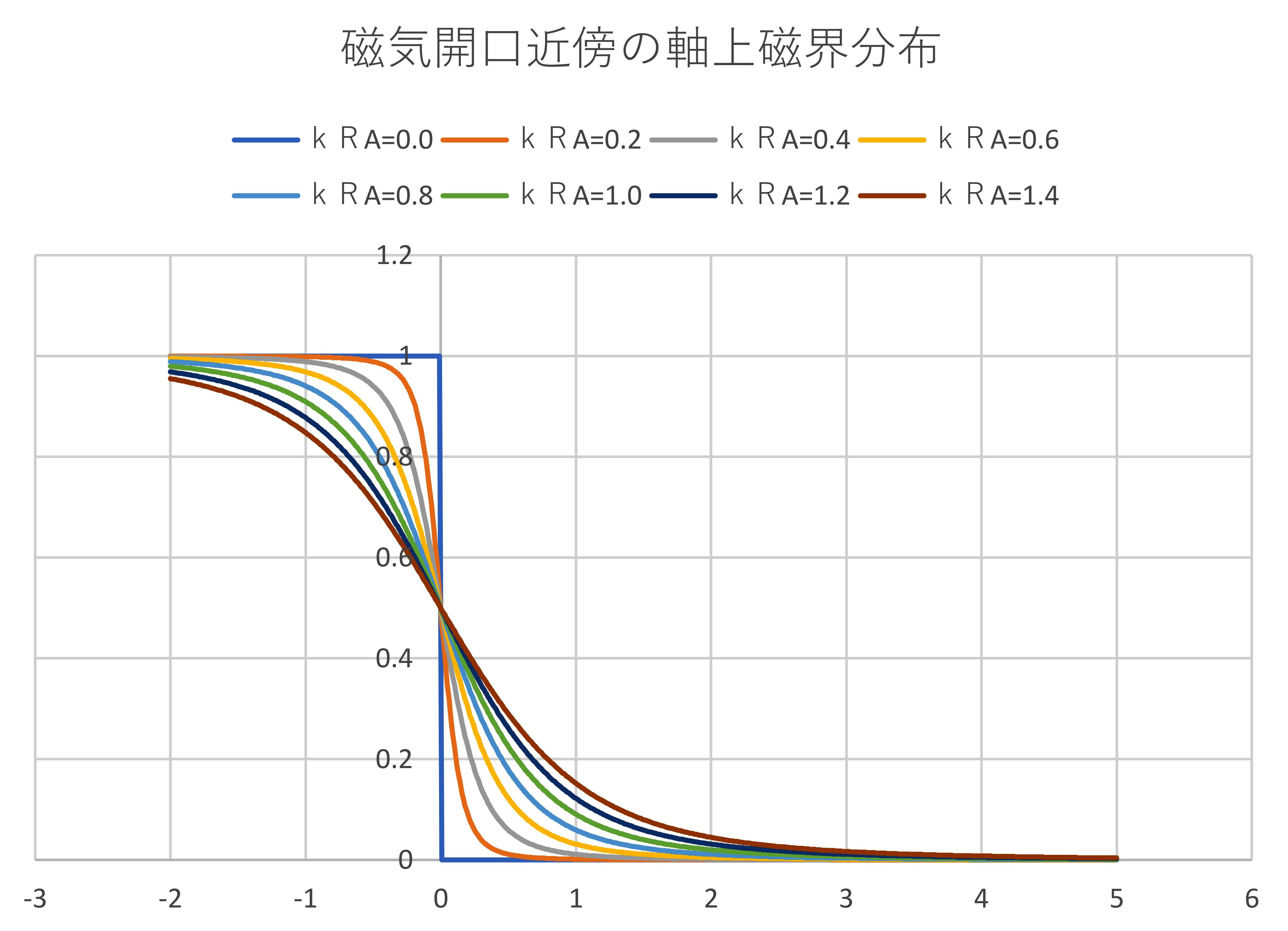 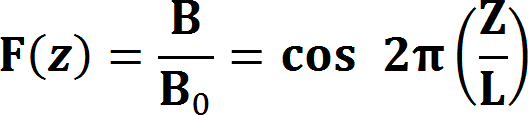 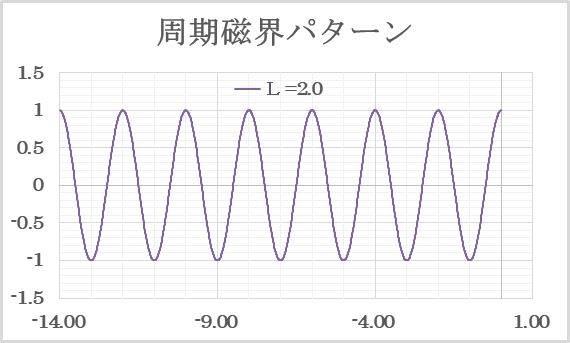 4.Mathieu方程式 正規化された近軸軌道方程式から、σ=R、ρ=2πZ/Lとおいて変形すると、 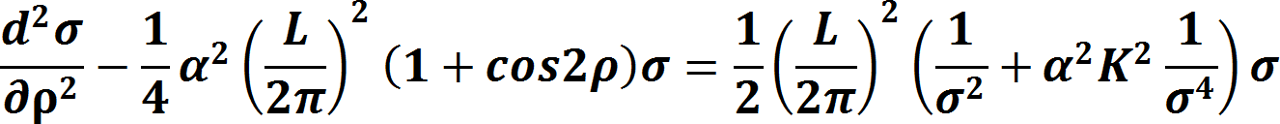 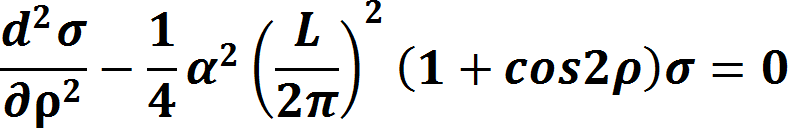 
 一般的な進行波管に用いられるPPM集束系では、次の第一安定域が使われている。 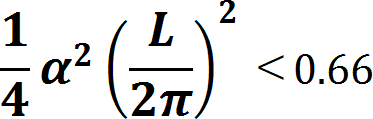 最初に、周期磁界の影響を受けない一様磁界(F(z)=1.0)の場合を考える。 この場合、電子ビームのうねり(リップル)を最小にする平衡条件は、 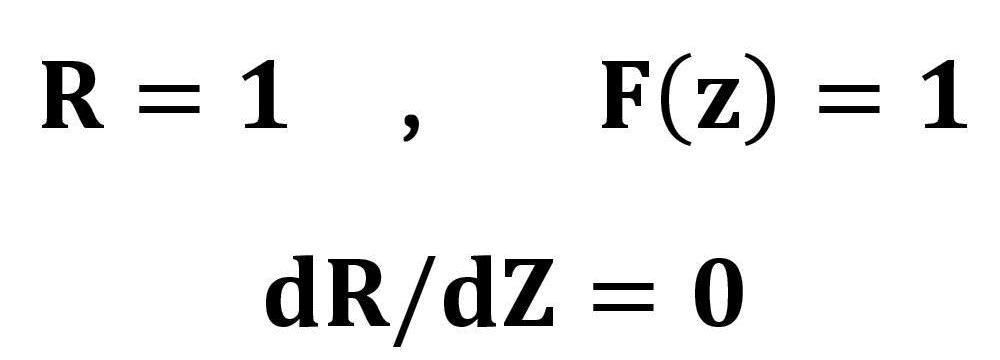 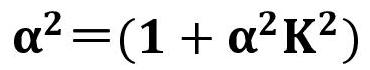 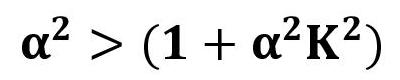 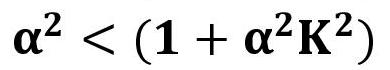  この事例では、α2=4の時、α2K2=3で、α2=1+α2K2 を満たし、電子ビームが基準ビーム径R=1 で平衡になる。 α2=4の時、α2K2=1or2 ならば、α2>1+α2K2 となり、基準ビーム径より小さいところで、電子ビームがうねる。 α2=4の時、α2K2=4or5 ならば、α2<1+α2K2 となり、基準ビーム径より大きいところで、電子ビームがうねる。 α2=6ならば、α2K2=2or3or4 の時、α2>1+α2K2 となり、基準ビーム径より小さいところで、電子ビームがうねる。 α2=6ならば、α2K2=6or7or8 の時、α2<1+α2K2 となり、基準ビーム径より大きいところで、電子ビームがうねる。 次に、周期磁界中での電子ビームのうねり具合いを考える。 この場合、電子ビームのうねり(リップル)を最小にする平衡条件は、  の時 の時
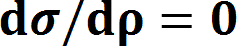 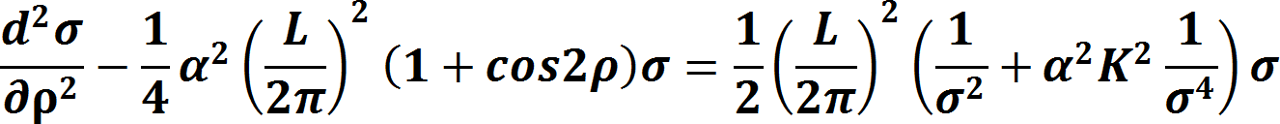 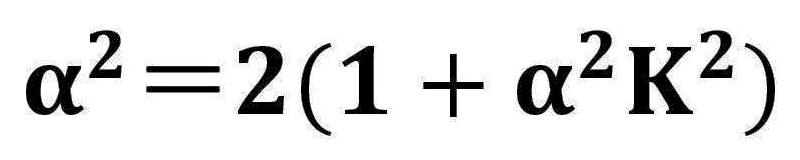 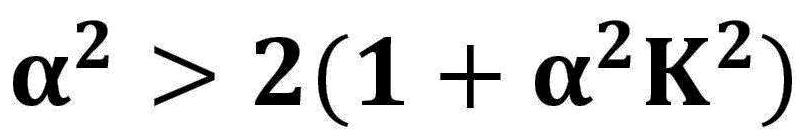 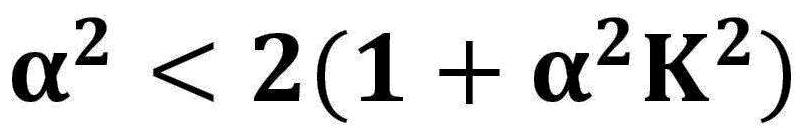  この事例では、周期磁界の波長L=1.4の場合であり、α2=10の時、α2K2=4 ならば、α2=2(1+α2K2) となり、基準ビーム径近傍で電子ビームのうねりが最小になる。 α2=10の時、α2K2=2or3 ならば、α2>2(1+α2K2) となり、基準ビーム径より小さいところで、電子ビームがうねる。 α2=10の時、α2K2=5or6 ならば、α2<2(1+α2K2) となり、基準ビーム径より大きいところで、電子ビームがうねる。 磁気開口を有する周期磁界中での電子ビームのうねり具合は次の図で示す。 この事例では、L=2.3、α2=4の時、α2K2=0.25,1.0,4.0 を変化させた場合である。  次に、周期磁界の波長の変化を考慮した電子ビームのうねり(リップル)について検討する。いま、電子ビームは、平衡条件式を満足しているとする。 すなわち、任意の周期磁界の波長において、うねり(リップル)が最小になる条件が整っていることになる。また、電子ビーム系は、第1安定域に存在するとすれば、 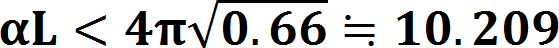      Mathieuの第1安定域の平衡条件を満たす範囲において、理想的な電子ビーム流で起こり得る周期磁界内でのリップル(うねり)の大きさは、αLの値に依存する。 次の図は、この場合リップル(うねり)の大きさの変化を示している。 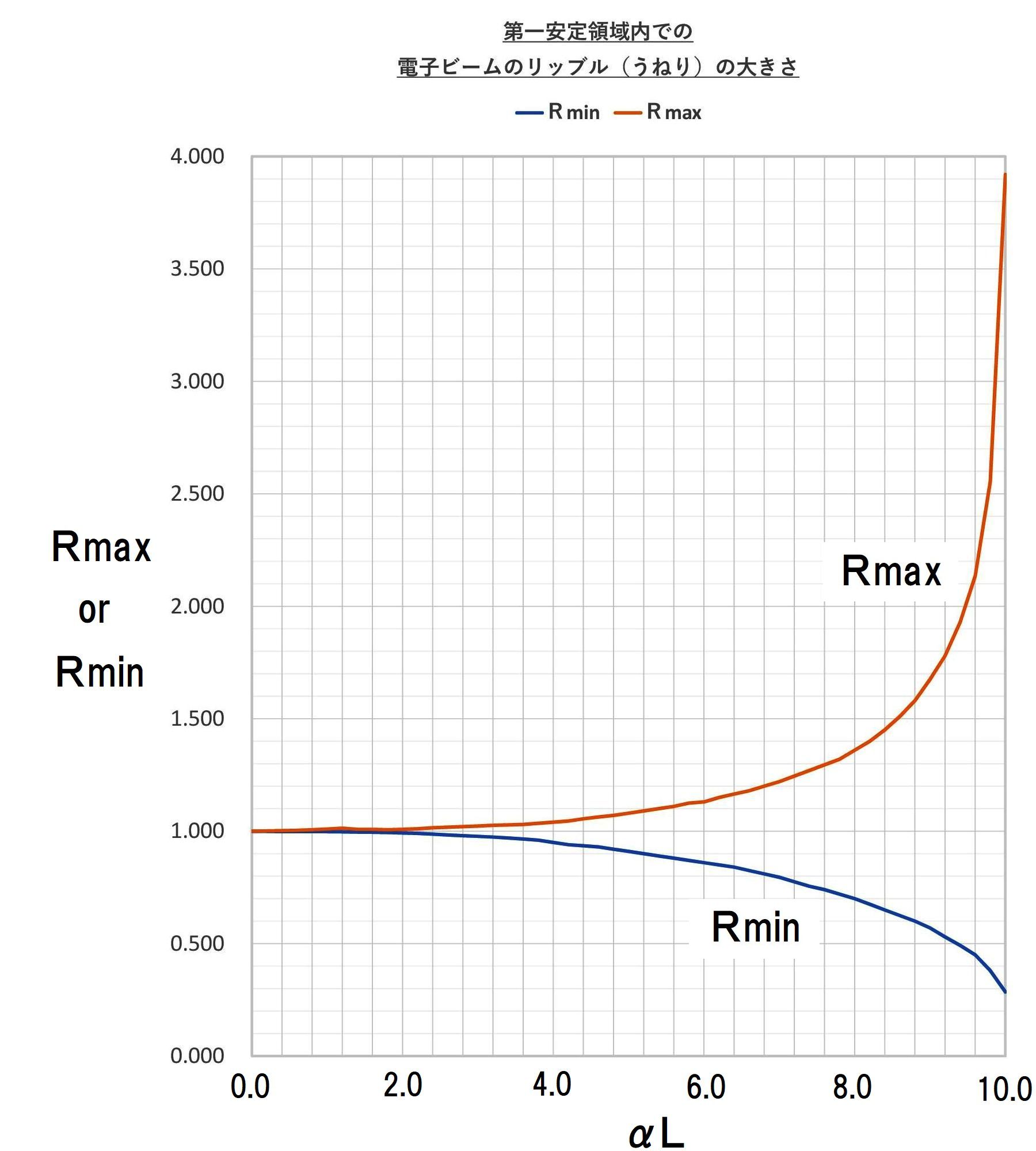 結局、周期磁界内で安定した実用的な電子ビーム流を得るためには、Mathieuの第1安定域を満たすだけでは不十分であり、 少なくとも電子ビームのうねり(リップル)を15%以内にするためには、  5.周期磁界と電子ビームとの整合 周期磁界と一様磁界との対応は、磁束密度の持つエネルギー平衡から考えられ、二乗平均値(r・m・s 値)の概念で説明できる。 いま、正規化された一様磁界をF0、周期磁界をF=B/B0=cosρとおき、周期磁界の一波長(ρ=0〜2π)の間で、二乗平均値(r・m・s 値)を考える。 この場合、 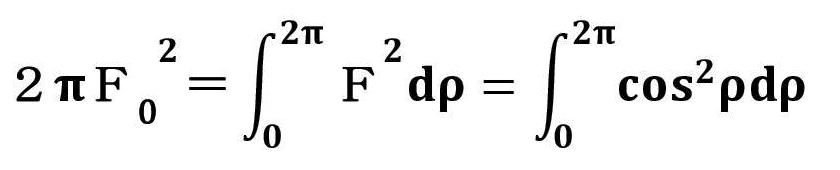 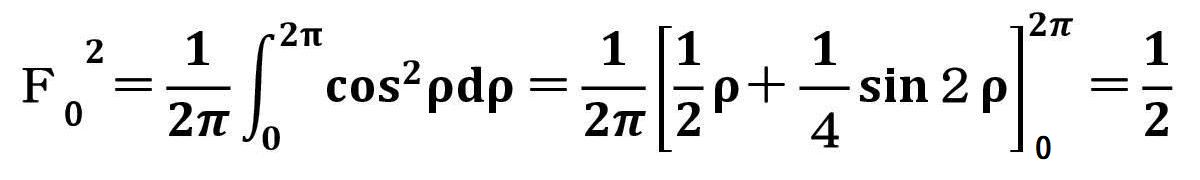 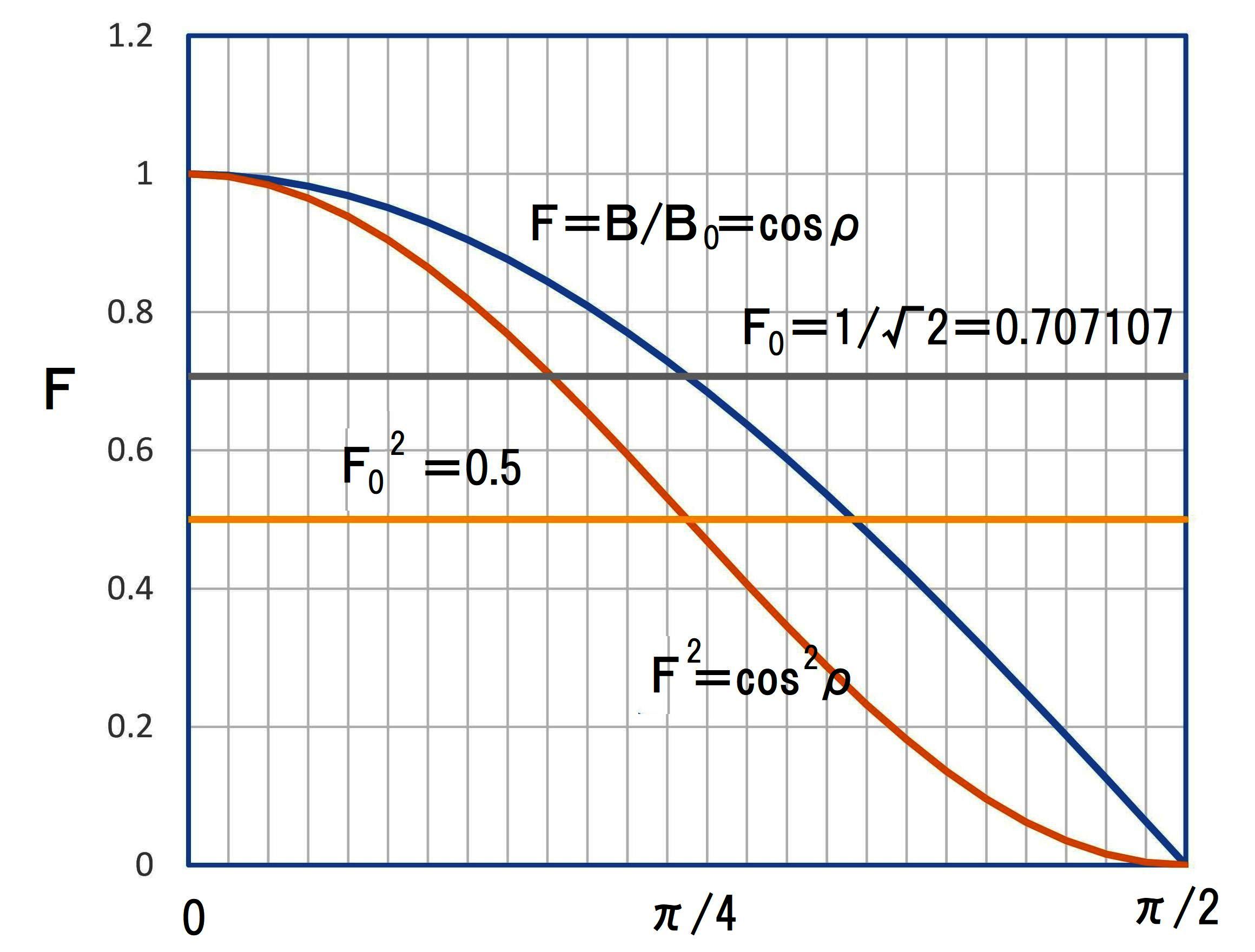 次に、これを電子銃近傍において考えてみる。一般のPPM集束の電子ビーム系のカソード位置は、正常な周期磁界の外に置かれている。 この場合、カソード磁界Bcと周期磁界のピーク値B0は、連続的にある。 したがって、この磁界パターンと電子ビーム流との対応は、一様磁界と同じように取り扱うことが困難である。 一様磁界の場合、電子銃の静電集束系から得られる電子ビーム流のビーム半径rと磁界パターンとの関係は、 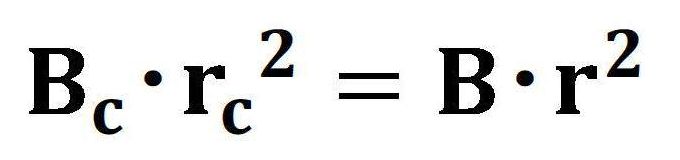
一方、周期磁界におけるカソードからの最初のピーク値Bmaxまでの磁界パターンをF(z)とおいて、
カソード面でz=0、最初のピーク値Bmaxの位置でz=z0と置き、先に説明した二乗平均値の概念を適用すると次式が成立する。
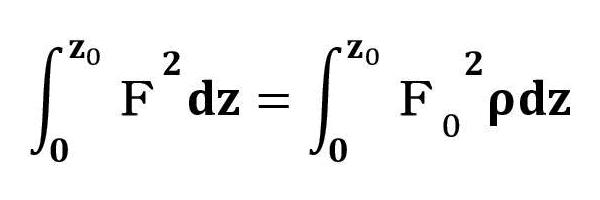
以上の手順について、具体的な事例に基づいて説明する。
いま、14GHz帯PPM集束の結合空洞型進行波管の電子銃近傍の電子ビーム流とその時の理想磁界パターンを考える。
次の図は、電子銃近傍の電子ビーム流と一様磁界に至る理想磁界パターンである。
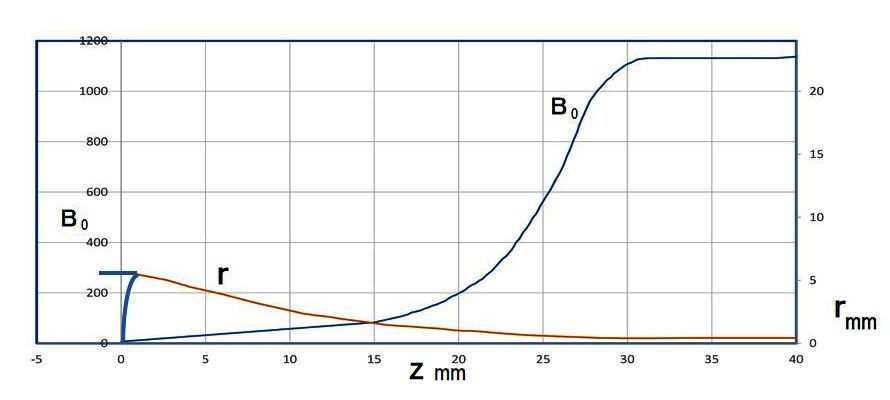
次に、周期磁界に至るまでの、現実の磁束密度分布を示す。
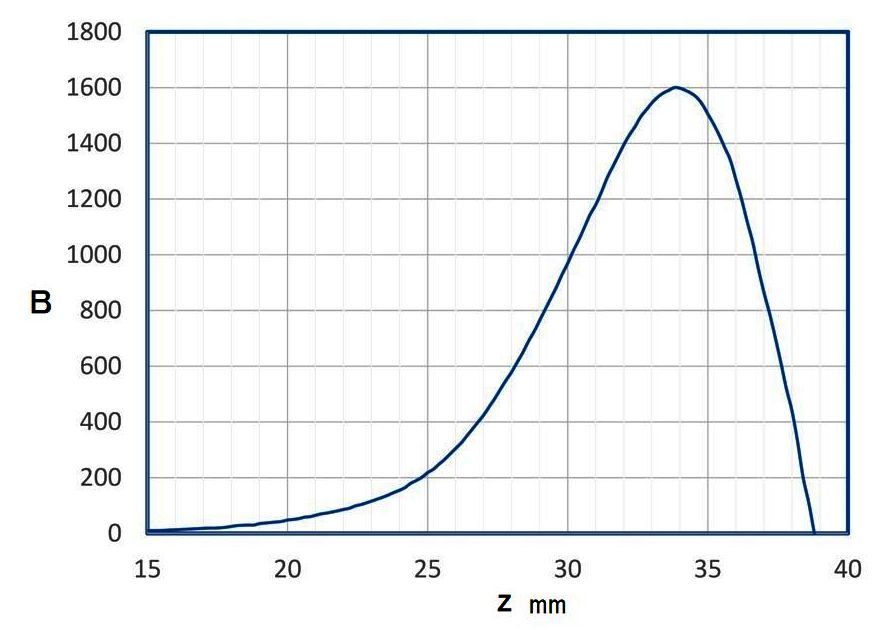
問題は、一様磁界に至る理想磁界パターンと周期磁界に至る現実の磁束密度分布の関係にある。
これを磁束密度の二乗平均値の関係で対応付け、それを次の図で示す。
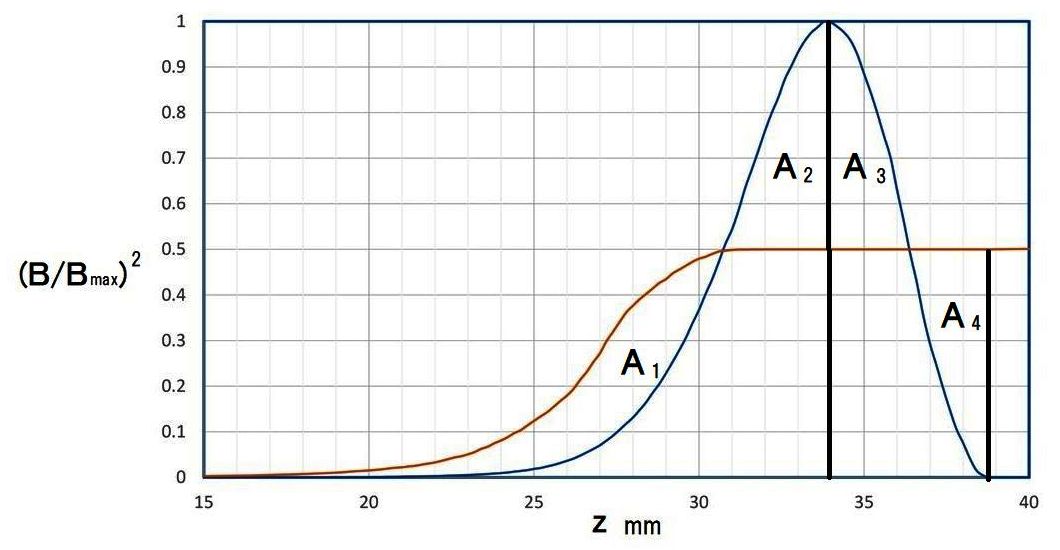
つまり、磁束密度の面積が、A1=A2,A3=A4を満たすように調整する。
このことで、かなりリップル(うねり)の少ない電子ビーム系が得られる。
これらのことから、周期磁界において、電子銃近傍で電子ビーム流と磁界パターンとの整合を取る方法は、基本的に二つの方法が考えられる。
一つの方法は、電子ビーム流を形成する電極構造と磁界パターンを形成するポールピースを含む磁気集束系との相対位置をz軸上でスライドして、
二乗平均値の整合関係を満たすやり方である。
もう一つの方法は、周期磁界におけるカソードからの最初の磁束密度のピーク値の強さを変更する方法である。
この方法は、磁束密度のピーク値を弱くすることで、前述の図において、A2の面積をA1の面積よりも小さくすることができる。
しかも、電子ビーム流の電極構造と磁気集束系が固定されている場合、外部から比較的容易に調整することが可能である。
しかし、最初の磁束密度のピーク値が変動することで、第二、第三の磁束密度のピーク値との関係をも考慮しなければならない。
さらに、磁束密度の二乗平均値の関係で対応付けられた磁束密度の面積Aiの絶対量は、z軸方向へ縮めて小さくすることにより、
先に示した電子ビームのリップルを小さくする平衡条件αLのLを小さくすることに相当する。
すなわち、磁束密度の面積Aiの絶対量は、できるだけ小さくすべきである。
このためには、電子銃部のポールピースの内径をできるだけ小さくするなどが必要である。
6.電子銃設計と静電集束電子ビーム系
次に、電子銃を設計する際の静電集束電子ビーム系で得る電子ビーム半径と周期磁界との平衡条件の関係について検討する。
電子ビームの進行方向に垂直な面内の電子分布が相対的に変化しないで輸送される条件はブリリアンフローと呼ばれる。
この条件を満足するはBrillouuin磁界は、電流密度との平衡条件を満たし、次式で与えられる。

通常、電子銃は、多孔質のタングステンに酸化バリウムなどを浸み込ませ、大幅な電子放出が可能な含浸型の球状カソード(陰極)が使用される。
しかし、カソード表面からの電子の引き出しは、熱電子放出によるが、得られる電流密度には限界がある。
このため、カソード半径は、電子ビーム流のビーム半径よりも大きくなり、カソードからの電子ビーム流は、磁界による集束が不可欠となる。
このような直線ビームは、進行波管やクライストロン(速度変調管)などのマイクロ波管に使われ、ピアス型電子銃で形成される。 この場合、ビーム径は、マイクロ波管の動作周波数に依存し、電子ビームがパイプ径の内側を通過する。 具体的には、マイクロ波管の動作電圧を決めて、マイクロパービアンスμPから電流を求める。 この時、電流は電圧の1.5(3/2)乗に比例する。これはMaxwellの方程式によれば、電荷密度が電圧に比例し、 電子運動によるエネルギー保存則から、電子の速度が電圧の平方根に比例するためと考えることができる。 一般に、電子ビーム流の電流と電圧の関係は、マイクロパービアンスμPと呼ばれ、次のパラメータで定義される。 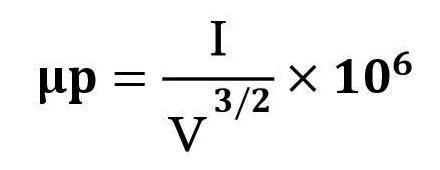
結局、カソード(陰極)から取り出せる電流密度jcに制約され、カソード半径rcが決まる。
さらに、適正な電子ビーム流のビーム半径r0とマイクロパービアンスμPの関係から、電子銃の形状が決まる。
この時、カソード半径rcは、
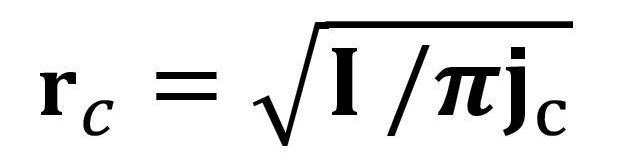
となる。
一様磁界の場合、電子銃の静電集束系から得られる電子ビーム流は、カソード上に磁場が無ければ、Brillouin磁界のビーム半径が最少となり、安定する。
この場合、一様磁界の磁束密度がBrillouin磁界より小さいと、ビームは広がり始め、平衡値を中心にうねり振動する。
また、磁束密度がBrillouin磁界より大きいと、ビームはさらに収束された後にうねり振動する。電子ビームの振動は、カソードからのビームの入射角によっても影響する。
電子ビームの中心軸がカソードの中心とズレがあったり、曲がっていたりしても電子ビームは振動やうねり(リップル)の原因になる。
この時、一様磁界B0とカソード上の磁界BcとBrillouin磁界BB、 および電子ビーム半径r0とカソード半径rcとの関係は、次式で与えられる。 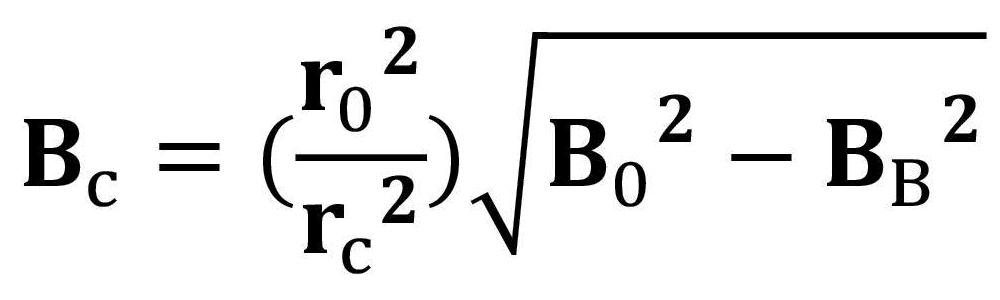
周期磁界においても、磁界の一部がカソード側に漏れ、カソード上に磁場が存在すると、電子ビームの振動は、Brillouin磁界の時よりも安定し易くなる。
この場合、電子ビームの集束が弱くなるが、一様磁界とカソード磁界およびBrillouin磁界との関係は、カソード径と電子ビームの平衡径との関係が次式で結ばれる。
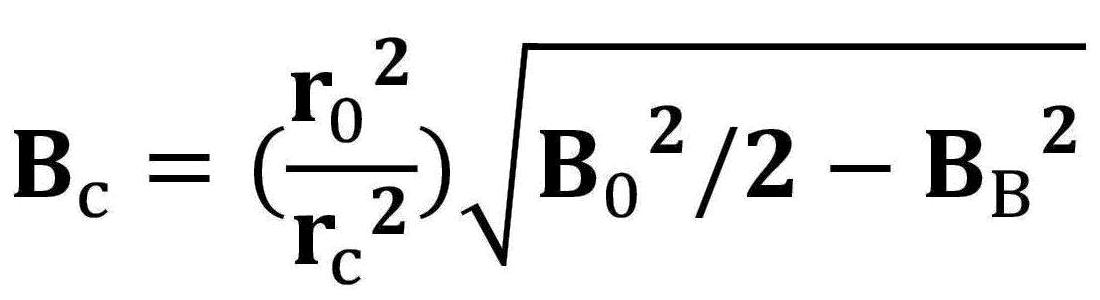 そして、カソード磁界Bcは、最小ビーム半径rminの位置から、一様磁界B0に接続される。 この時、正規化された磁界パターンは F(z) とする。 一方、静電集束の電子ビーム系は、電子ビーム流と理想磁界パターンとの関係式が 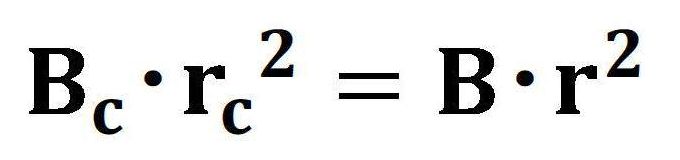 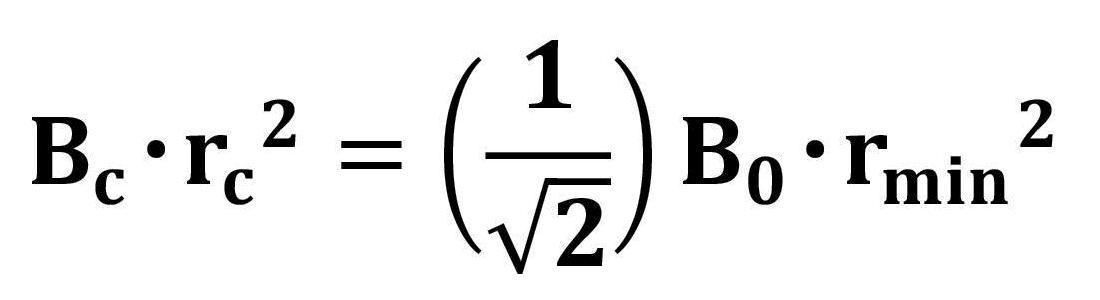 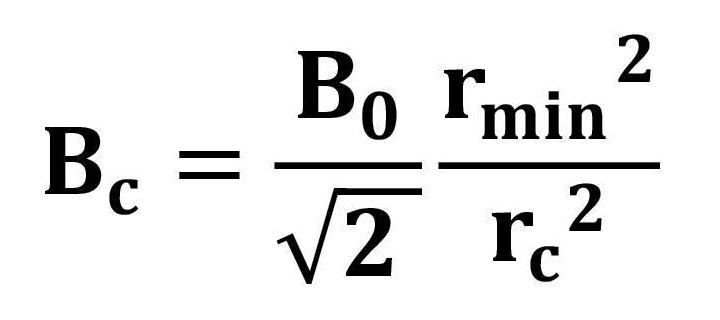 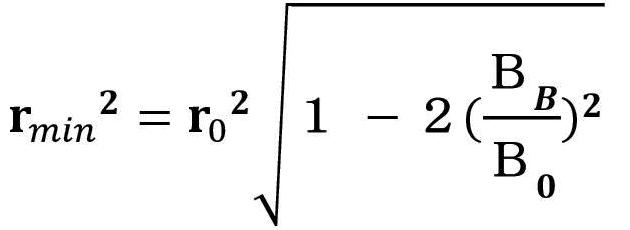 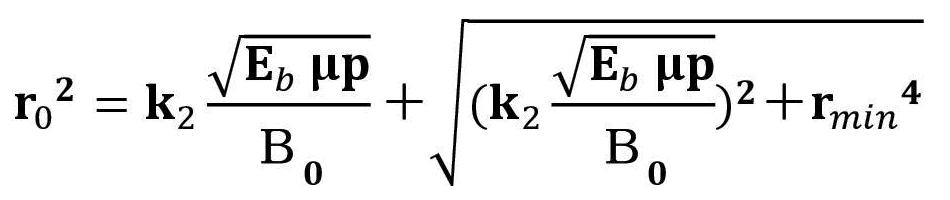
7.むすび 以上、周期磁界における電子ビーム系の安定性および電子銃近傍での磁界パターンと電子ビーム流との整合について述べた。 この結果、 (1) 電子ビームの平衡条件は 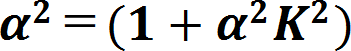 で表せる。
この平衡条件から外れると、電子ビームのリップル(うねり)は大きくなる。 で表せる。
この平衡条件から外れると、電子ビームのリップル(うねり)は大きくなる。
(2) 周期磁界中において、電子ビーム流の安定性は、Mathieu方程式の第一安定域を満足するだけでは不十分である。 実用的には  の領域を満足すべきである。 の領域を満足すべきである。
(3) 周期磁界と一様磁界とは、二乗平均値(r・m・s値)で対応付けられる。ここでは、この考え方に基づいて、周期磁界と電子ビーム流とを整合させる方法を確立した。 と云える。しかし、周期磁界中において、最適な電子ビーム流を得るためには、ここで述べた以外の設計パラメータについても検討しなければならない。
次の資料は、この報告に基づき、周期磁界を用いた過去の代表的なN社の進行波管の電子ビーム系の安定性に関するパラメータを示している。
(文責:yut) |