| 佺 | a-x | 倓倶乛乮倎亅倶乯亖倠佺 | t | 倓倲 | a | 0 |
丂偟偨偑偭偰丄ln(倎乛乮倎亅倶))傪倲偵懳偟偰僾儘僢僩偡傟偽丄尨揰傪捠傞捈慄偑摼傜傟丄偦偺岡攝倠偑堦師斀墳偺懍搙掕悢偵側傞丅 傑偨丄愊暘傪倶侾偐傜倶俀丄倲侾偐傜倲俀傑偱偲偡傟偽丄
偲側傝丄擟堄偺俀偮偺擹搙應掕偐傜懍搙掕悢偑媮傑傞偙偲偵側傞丅
丂師偵丄擇師斀墳乽俙亄俛仺俠亄俢乿傪峫偊傞丅倲亖侽偺帪丄乽俙乿偺弶婜擹搙倎丄乽俛乿偺弶婜擹搙倐偲偡傞丅帪娫倲偑宱夁偟偨帪丄 乽俙乿偍傛傃乽俛乿偺倶偑斀墳偟偰丄乽俠乿偲乽俢乿偑倶偩偗惗惉偝傟偰偄傞偙偲偵側傞丅偙偺応崌丄擇師斀墳懍搙幃偵側傝丄
偑惉棫偡傞丅曄悢暘棧偡傟偽丄
偲側傝丄愊暘偡傟偽丄偮偓偺擇師斀墳懍搙幃傪摼傞丅
丂偮傑傝丄擇師斀墳懍搙幃偵廬偆応崌丄帪娫倲偵懳偡傞偙偺捈慄偺岡攝偐傜丄懍搙掕悢偑摼傜傟傞丅側偍丄倎亖倐偺応崌丄
偱偁傝丄愊暘偡傞偲丄師偺傛偆偵側傞丅
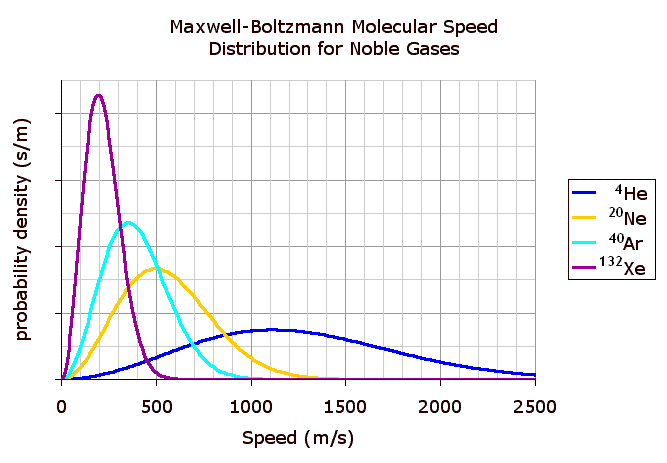
丂堦斒偵丄斀墳傪懍偔偡傞偵偼壏搙傪崅偔偡傞丅椺奜揑偵丄壏搙傪崅偔偡傞偲丄斀墳偑抶偔側傞偙偲乮椺丗峺慺怗攠斀墳乯傕偁傞丅 擹搙傗偦偺懠傪堦掕偵偟偰丄壏搙偩偗曄壔偝偣傞偲丄斀墳懍搙偑巜悢娭悢揑偵憹壛偡傞丅侾俉俉俋擭偵傾儗僯僂僗 乮S.Arrhenius:1859-1927乯偼丄壏搙俿偲斀墳懍搙掕悢倠偺娭學偑師幃偵側傞偙偲傪尒晅偗偨丅
亖俙exp(亅俤乛(俼俿))
丂偡側傢偪丄乽log倠亖兛亅兝乛俿乿偼乽倠亖俙exp(亅俤乛(俼俿))乿偲昞尰偱偒丄傾儗僯僂僗偺幃偲屇偽傟偰偄傞丅 偙偙偱丄倠偼斀墳懍搙掕悢丄俤偼妶惈壔僄僱儖僊乕丄俙偼壏搙偵柍娭學側掕悢偱昿搙場巕乮帪娫偺媡悢乯丄俼偼婥懱掕悢丄 俿偼愨懳壏搙偱偁傞丅側偍丄昿搙場巕俙偼丄堦師斀墳乮侾暘巕斀墳乯偺応崌丄帪娫偺媡悢偱偁傝丄怳摦悢偱偁傞丅 擇師斀墳乮俀暘巕斀墳乯偺応崌丄徴撍昿搙傪昞偟丄徴撍偟偨帪偵壗亾偑斀墳偡傞偐傪堄枴偟偰偄傞丅 偮傑傝丄昿搙場巕俙偼丄婥懱暘巕塣摦榑偺徴撍悢偱偁傝丄懡棻巕宯偺儃儖僣儅儞摑寁乮妋棪乯偵廬偆丅
丂側偍丄傾儗僯僂僗偺幃偼丄帺慠懳悢偺宍偵偡傞偲
偲側傝丄師偺傛偆偵曄悢傪偲傟偽懳悢僌儔僼偱 倷亖倣倶亄倐 偺捈慄偵側傞丅
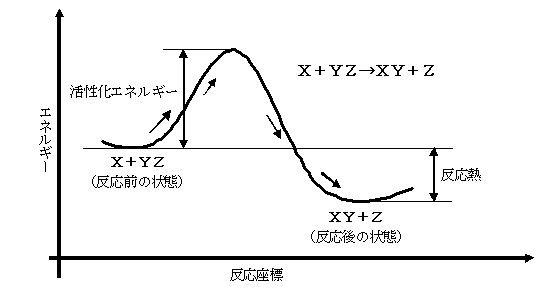
丂斀墳夁掱傪斀墳暔乽俙乿偐傜斀墳偺拞娫懱乽俛乿傪宱桼偟偰惗惉暔乽俠乿偵側傞宱楬傪峫偊傞丅
丂偙偺応崌丄斀墳偼乽俙仺俛乿偲乽俛仺俠乿傪暿乆偵峫偊傞丅偲偡傞偲丄
倓乵俙乶乛倓倲亖亅倠1乵俙乶
倓乵俛乶乛倓倲亖倠1乵俙乶亅倠2乵俛乶
乵俠乶亖乵俙乶0亅乵俙乶亅乵俛乶
偺娭學幃偑惉棫偡傞丅偙偺曽掱幃傪夝偔偲丄
乵俙乶亖乵俙乶0exp(亅倠1丒倲)
倓乵俛乶乛倓倲亖倠1乵俙乶0exp(亅倠1丒倲)亅倠2乵俛乶
丂偙偙偱丄乵俛乶亖倶丒exp(亅倠2丒倲)丂偲偍偔偲丄
倓倶乛倓倲亖倠1乵俙乶0exp(亅(倠1亅倠2)丒倲)
倶亖亅(倠1乛(倠1亅倠2))乵俙乶0exp(亅(倠1亅倠2)丒倲)亄const
乵俛乶亖{亅(倠1乛(倠1亅倠2))乵俙乶0exp(亅(倠1亅倠2)丒倲)亄const乸exp(亅倠2丒倲)
丂倲亖侽偺帪丄乵俛乶亖侽偲偟偰丄乵俙乶乛乵俙乶0亖exp(亅倠1丒倲)
乵俛乶乛乵俙乶0亖(倠1乛(倠1亅倠2)){exp(亅倠2丒倲)亅exp(亅倠1丒倲)}
乵俠乶乛乵俙乶0亖侾亅乵俙乶乛乵俙乶0亅乵俛乶乛乵俙乶0
亖侾亅exp(亅倠1丒倲)亅乷(侾乛(侾亅倠2乛倠1)){exp(亅倠2丒倲)亅exp(亅倠1丒倲)}乸
丂嬶懱揑側帠椺偲偟偰丄乽倠2乛倠1亖侾乛俁乿偲乽倠2乛倠1亖侾侽乿偺応崌偵偮偄偰寁嶼偡傞丅
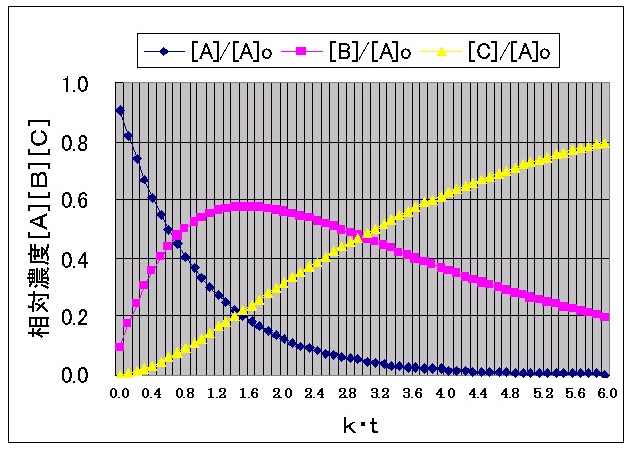
恾亅俆丂乽倠2乛倠1亖侾乛俁乿偺応崌
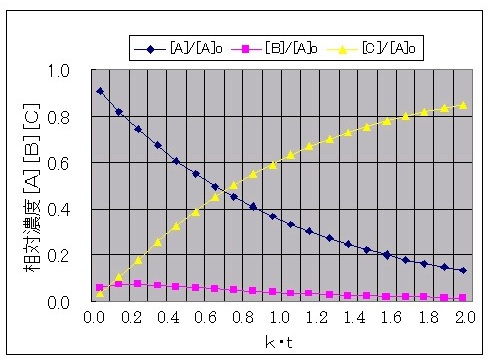
恾亅俇丂乽倠2乛倠1亖侾侽乿偺応崌
| 丂丂倠1 | 丂丂倠2 | |||
| 俙 | 丂仺丂 | 丂俛 | 丂仺丂 | 丂俠 |
丂偙偺応崌丄斀墳偼乽俙仺俛乿偲乽俛仺俠乿傪暿乆偵峫偊傞丅偲偡傞偲丄
偺娭學幃偑惉棫偡傞丅偙偺曽掱幃傪夝偔偲丄
丂偙偙偱丄乵俛乶亖倶丒exp(亅倠2丒倲)丂偲偍偔偲丄
丂倲亖侽偺帪丄乵俛乶亖侽偲偟偰丄
亖侾亅exp(亅倠1丒倲)亅乷(侾乛(侾亅倠2乛倠1)){exp(亅倠2丒倲)亅exp(亅倠1丒倲)}乸
丂嬶懱揑側帠椺偲偟偰丄乽倠2乛倠1亖侾乛俁乿偲乽倠2乛倠1亖侾侽乿偺応崌偵偮偄偰寁嶼偡傞丅

恾亅俆丂乽倠2乛倠1亖侾乛俁乿偺応崌

恾亅俇丂乽倠2乛倠1亖侾侽乿偺応崌
乮暥愑丗倷倳倲乯