本稿は現在執筆中の『水中泳の科学 — スポーツジムのプールを120%楽しむ (仮題) 』の補注または付録として用意したものです。単独の論文としてもいくらかの価値があろうかと、ここに掲載します。
何事をも発見することなく長々と大問題について
議論するよりも、私はむしろ、たとえ小さなことでも
一つの事実を発見するほうがよいと思う。
— ガリレオ・ガリレイ
("Feynman's Lost Lecture" 砂川重信訳 岩波書店 より)
アルキメデス神話
浮力と聞くと、誰もが「アルキメデスの原理」をまず思い浮かべることでしょう。その原理とは
「液体中の物体は、その物体が押しのけている流体の重量と同じ大きさで上向きの浮力を受ける」というもので、アルキメデスが発見したと言われています。しかし、これを最初に定式化したのがアルキメデスだったとしても、実際に彼が「発見した」かどうかは疑問です。というのも、風呂の水が溢れるのを見て発見したという伝説 (*1) は、この原理とは結びつかないし、彼がこの原理を定式化した著作『浮体について』の中で与えている証明は、新しい原理を発見した、というよりも、すでに知られていた経験的事実に数学的根拠を与えようとしているように見えるからです。
そのことは、証明に使われている幾何図形 (*2) がわざわざ球面としての海水面を想定した特殊なケースであること、そのためか現代では「アルキメデスの原理」の説明にこの図を持ち出す学者も教師もいないこと、などからもうかがえます。『浮体について』というタイトルからは、そもそものアルキメデスの関心は船が安定して浮かぶ原理にあったのではないかという想像もはたらきます。それが「物体が押しのけている流体」(*3) という表現にも現れています。
ここで浮力を論じるのは、もちろん船のためではありません。スイマーとして、水の中の自分自身の身体がどのような浮力を受けているのか、について理解するためです。せっかくプールに入るのですから、泳ぐということと浮力がどう関係するのか、さらに浮力と同時に浮心について知るのも楽しい発見だと思っていただくことが、この補講の目的です。
そのためには、アルキメデスの名を封印したいと思います。というのも、そもそも「水中の物体が同体積の水の重さに等しい浮力を得る」ことは、ちょっと考えれば、当たり前だと分かることであって、わざわざ古代ギリシャの数学者の権威にすがる必要はないからです。その「当たり前」を説明するには、以下の2つの公理を認めれば十分です。
公理1: 静止している水は自ら動き出さない。
公理2: 水の密度はどこでも一様である。
ここでは単純化のために水に限定して議論します。液体一般や大気にも拡張するのは容易だから。
定理1:
水中で静止している立体は、同じ体積分の水の重量に等しい浮力を受けている。
(ここで立体とは、一定の体積と形状を持つ均質の物体・物質のこと)
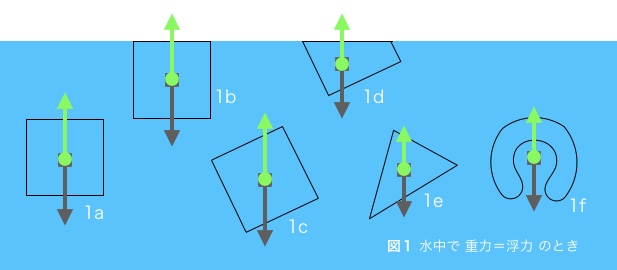
静止している水の中に、単位区画(簡単のために、例えば一辺10cmの立方体)を考える。この区画を厚みが極小で、かつ変形しない膜で覆った立方体とする。もし、この仮想立体が想像しにくいなら、その体積が変化することなく凍った氷を考えると良い。この立体は公理1、2から、どの位置でも、どのような姿勢でも水中で静止する。また、水面に接した位置(図1b)でも静止する。(*4)
立体が静止しているのは、立体の重量、すなわち同体積の水の重力(この例では1Lで1kg)に対し同じ大きさで反対向きの力 — 浮力 — がはたらいているからに他ならない。今立体は水で満たされているが、比重が水と同じであれば、どんな物質であろうと静止することに変わりはないし、容積が同じであれば、同じ浮力を受けることに変わりはない。
もともと静止している水を仮想的な膜で区画しているだけなので、公理により、この仮想物体はどのような形状(図1d, 1e, 1f)であっても上の議論が成り立つ。
物体でなくても、魚が水中で静止できるのは浮力を自ら調節しているからで、死んでしまうと浮かび上がったり、水底に沈んでしまいます。スクーバダイビングでは肺の中の空気量の加減とBC(浮力補正ジャケット)により自身の体積をコントロールすることで、水中で静止するトレーニングが必須です。
定理2:
水中で静止するこの立体にはたらく浮力の集中点(浮心)は立体の重心に一致する。
重心はその姿勢により変化しない。立体は静止しているのだから、浮力は常に重心を通る垂直線上にはたらいていることになる。したがって、重力の中心点としての重心と浮力の中心点としての浮心は一致する。重心も浮心も力の仮想的な作用点、支点であるので、立体の内部ではなく、その外部(空間)に位置することもあり得ます(図1f)。体操の鉄棒における「蹴上がり」では、体をくの字にすることで、重心を鉄棒に近づけて回転を容易にしています。言い換えると、浮心の位置を求めることは、その立体の重心の位置を知ることに帰着する。
定理3:
水中で静止できない立体は、自身にはたらく浮力よりも、自身の重量が大きいか、小さいか、のどちらかである。
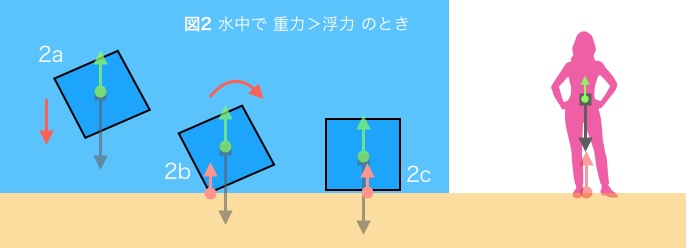
前者の場合、立体は沈下し、水底に達する。その時は、立体の重力が浮力と水底からの抗力に釣り合った状態で静止する(図2c)。
これは地上で立って静止している私たちの姿と同じ。私たちは空気の「海」の海底にいるので、大気の浮力を受けている。大気の地上での重さは1g/L 程度。体重計で60kgであっても、それは大気による浮力60g(人体の比重はおおよそ1。体重60kgの人の体積はおよそ60L)を差し引いた数値。つまり、人にかかる重力は60.06kg、それが大気による浮力60gと地面からの抗力60kgに釣り合って静止している。ただ、大気は水に関する公理2が該当しない。
後者の場合、立体はその一部を水面上に出すことで減少した浮力が立体の重力と等しくなるまで浮上する。本稿では浮上して浮いている立体、つまり水面上の人体、が関心事なので、浮体がどのように静止するかを考える。
定理4:
浮体にはたらく浮力は、水面下にある立体部分の体積に等しい水の重量である。このとき、立体が持つ重心と、立体の水面下部分が持つ浮心とでは、その位置が異なる。
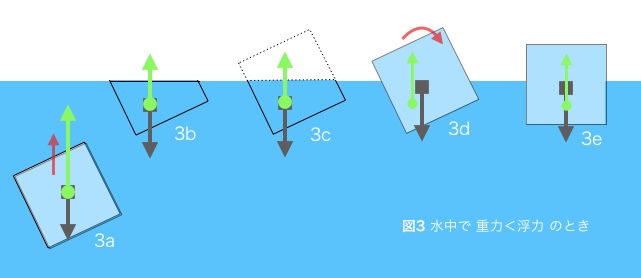
定理1で示した図1d では立方体を斜に切り取った立体が水面に接して静止している。このとき重心と浮心は一致している。今この立体に、切り取った部分と同じ形をして、かつ重さを持たない立体を貼り付けて立方体の外観を復元したとする。(図3c) これが想像しにくいなら、厚みのないプラスチックケースのような工作品を取り付けたと考えれば良い。するとこの復元した立方体の重心と浮心は元のままであり、静止したままとなる。ここで、立方体全体の重量を変えずに、密度を下げた均一の物質で満たしたなら、重心は立方体の中心に移動する。すると浮心とのずれにより右回りの回転モーメントが生ずる。(図3d) 回転に伴い、立体の水面下にある部分の容積は変わらないが、その形状が変化するので、浮心が移動する。(図3e)アルキメデスは浮体としての船の安定した静止条件に関心があったと思われますが、高層建築のようなフェリー船が横倒しになって転覆しないのは、重心は浮心よりも上にあるが、船がある程度傾いても浮心が移動して、重心(を通る鉛直線)よりも外側に来るように設計されているからです。そのため船の姿勢を元に戻すようにモーメントが生ずる。(図3d, 3e) このとき、重心の位置が重要なので、積荷や車両はその重量に基づいて配置、固定されます。同じ船でもヨットはセンターボードの下部に錘をつけて重心を下げた設計なので、傾いたり横転しても、常にヤジロベエのように復原力がはたらき、起き上がる。このように立体が水面上に一部を出すと、一般に浮心は重心と一致しない。立体が静止するには、浮心と重心が同じ鉛直線上にあって、かつそこから変位したときには元に戻そうとするモーメントがはたらくことが条件になる。(球体は完全に対称な立体なので特殊な例となる)
この重心と浮心の計算と積荷の重量配分を間違えた船はしばしば転覆し、中には進水式で海に出た新造船がいきなり沈没した例も歴史の記録に残っています。
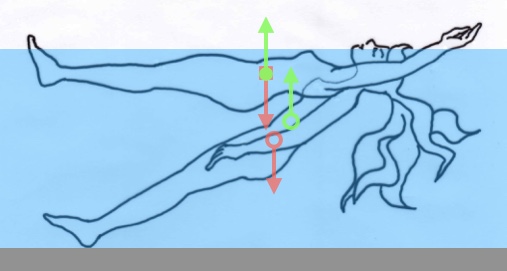
浮体としての人体が水面から出す体の一部というのは、まずは呼吸のために持ち上げる頭部、そしてクロールや背泳ぎ、バタフライにおけるリカバリー時の腕が典型的なものです。その腕の位置と動きが浮心と浮力にどう関係するかを本編で論じます。
豆知識1 水中は無重力の世界?
スクーバダイビングをおやりになった方はご存知ですが、水中で浮きも沈みもしないように浮力を調節した状態を「中性浮力」と呼びます。Neutral buoyancy の直訳です。このとき、宇宙空間にいるかのような無重力感があり、また実際にも宇宙飛行士のトレーニングを水中で行うこともあるので、この中性浮力を無重力状態と錯覚する人もいます。でもこれは間違いで、重力がなくなっているわけではありません。簡単に理解するために、ペットボトルに海水を満たし、その中にビー玉を一つ入れてフタをしたとします。当然ビー玉はボトルの底に沈みます。このペットボトルを抱えて海に潜って中性浮力を得ると、ビー玉はどうなるか? もちろんボトルの底に沈んだままです。ではこのビー玉入りボトルを宇宙ステーションに持ち込んだらどうなるか? ビー玉はどっちが底だか分からなくなります。でもこのボトルをグルグル振り回すと、遠心力という見かけ上の重力場が生まれて、ビー玉は「底」に落ちて行くでしょう。また宇宙でなくても、このボトルを持ってエレベーターに乗った時、不幸にしてエレベーターのロープが切れて自由落下を始めたとしたら、体は宙に浮き、ビー玉も水中で浮く無重力状態が体験できるでしょう。
豆知識2 水圧
浮力を立体にかかっている水圧の差分として解析的に説明しようとする人もいます。それも一つのアプローチではありますが、必ずしもスイマー向けとは思えません。「浮心」の導出がないからです。けれど、水圧そのものの理解は大切で、ときに命に関わります。水圧は深さ10mごとに1気圧増加します。地上の大気圧は1cm2当たり約1kg。空のペットボトルを水深10mに持ち込むと、水圧は2気圧の2kg/cm2。ペットボトルは容量が半分に潰れてしまいます。こうしたことからフリーダイビング(空気ボンベを使わない素潜り)で潜れる深さの限界は40mほどだと長く考えられていました。肺がペットボトルのように潰れて肋骨が折れてしまうと思われたからです。ところが、ダイバーはそれを超える深みに到達して、今や記録は100mを超えています。それは、腹部の内臓が横隔膜ごと肺に向かって押し上げられて、肺が縮んでも胸部が潰れるのを防いでいるから、という人体の驚異的な能力が分かりました。
これと逆のケースが、水底から水面に浮上するときの水圧差です。一例として、車に乗ったまま海に落ちて、海底10Mに沈んでしまったケースを考えます。車内の気圧が2気圧になるまで勢いよく海水が侵入してきて、やがて車内の空気は圧縮されて半分(以下)になりますが、外部の水圧と車内の気圧が同じになれば、ドアが開けられます。すると浮上に備えて息を大きく吸ってからドアを開けて海面を目指して泳ぎだすのが一般です。しかし、息を止めたまま浮上すると死に至ります。2気圧でいっぱいの肺が、1気圧の水面に近づくにつれて、2倍に膨れ上がって肺が破裂してしまうからです。スクーバダイビングの教習課程には、6〜10Mの水底にボンベ、BC、レギュレーター、ウエイトを置いて、口から空気を吐き出しながら浮上する緊急時対応の訓練が組み込まれています。
シュノーケルを使ったことのある人の中には、この管を長く伸ばせば、忍者さながらに水深1m、2mの深みに潜むことができるのではないか、と想像したことがある方もいるでしょう。けれど、これは掃除機を口に咥えるようなもので、肺胞が飛び出る危険性さえあります。
(*1)
アルキメデスがこの原理を発見したとされるエピソードとして、次のような逸話が伝えられています。金細工師に純金の王冠を作らせた王が、出来上がった王冠は純金ではなくて混ぜ物をして金をこすねたのではないかと疑い、アルキメデスに王冠を溶かすことなく、真偽を調べよと命じる。困り果てたアルキメデスは、ある日風呂に入ったときに、湯船から湯が溢れ出るのをみて、「分かったぞぉー(ヘウレーカ)」と叫びながら風呂から飛び出して、裸のまま通りを走った。しかしどう読んでも、これは浮力の原理の発見ではなくて、比重の違いを利用すればいいんだ、と気づいただけのことです。主な金属の比重 (g/cm3) を重いものから並べると、金Au 19.3、鉛Pb 11.4、銀Ag 10.5、銅Cu 9.0、鉄Fe 7.9。すると、もともと細工師が預かった純金が例えば4kgだったとすると、その体積はおよそ200g相当の水、つまり200cc、カップ1杯分です。けれど、もしも金を半量の2kg、残り2kgに鉛か銀かを使って4kgにしていたとすると、その体積は300cc弱。だから4kgの金塊と4kgの王冠を天秤に吊るして水中に沈めると、体積も同じかどうかが分かる。つまり、この時代すでに「比重」または「密度」の概念があったこと、水中にある物体はその容積に応じて重量が軽くなることは知られていたことがわかります。けれど、このことは、必ずしも浮力が「物体が押しのけている流体の重量と同じ」であることを示すものではありません。多分それは経験則として周知だったのだろう、とわたしは考えます。
(*2)
アルキメデスは『浮体について』(英訳 On Floating Bodies) の中で次のよう述べています。Proposition 5証明に添えられた図と英訳テキストの一部を以下にコピーします。(記号にラテン文字が使われているが、原典ではギリシャ文字か)
Any solid lighter than a fulid will, if placed in the fluid, be so far immersed that the weight of the solid will be equal to the weight of the fluid displaced.
定理5
ある液体よりも(比重が)軽い任意の立体は、その液体の中に入れられると、立体はその重さが、押しのけている(取って代わった)液体の重さと同じになる深さまで沈む。
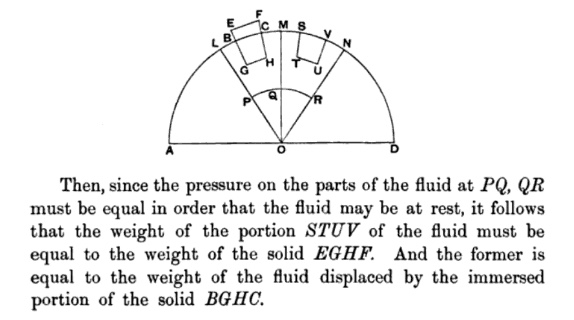
円弧AMDは地球の海面、EGHFは海面に浮いている立体、BGHCはその立体の水面下部分、STUVはその水面下部分をコピーした「海水区分」。立体と海水区分は、等しい底面から等しい水圧(浮力)を受けて静止しているので、立体の重さは「海水区分」つまり「押しのけた液体の重さ」と同じ、という論理。あえて重力方向の線と面で立体と液体を囲うのは、浮力を底面からの水圧のみに単純化するためでしょうか。そう思うと、これは新発見の証明というより、誰からも反論や反証のない既知の原理に、幾何学的な追認を与える試みのように見えます。
(*3)
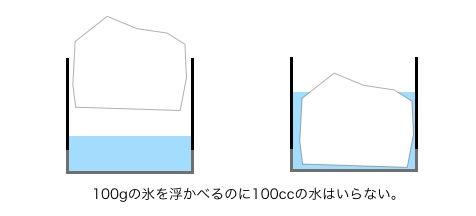
「物体が押しのけている流体の重量」という表現は必ずしも正確とは言えません。例えば、氷の比重を0.9 としたとき、体積150cc、重さ135gの氷は浮かぶために135ccの水を押しのける必要はありません。80cc程度の水だけでもコップの中で浮くことが可能です。
(*4)
このように、実際に実験を行わずとも想像上で「実験する」ことはしばしば「思考実験」と呼ばれます。有名な思考実験の例はガリレオ・ガリレイの落下実験で、彼はピサの斜塔から重さの異なる2つの鉄球が同時に地上に落下することをデモンストレーションした、という伝説がありますが、そもそも彼にはそんな実験をしなくても、二つが同じように落下することは分かっていたのです。今同じ重さの鉄球を2つ用意したとする。この2つに違いはないのだから、一緒に落とせば一緒に地表に到達することは自明である。ではこの2つを棒で繫いで、もう一つの鉄球と一緒に落としたらどうなるか? — こうガリレオはその著書『新科学対話』の中で「実験」して見せています。
[HOME] > [楽しいバイクライフのために]