バネ下重量という用語があります。車でいうと、そのサスペンションから下、つまり、ホイール、タイヤ、ブレーキなどの加算重量です。このバネ下重量は小さいほどいい、という文脈で使われるのが普通です。単純に考えて、車の走行中、その本体と乗員が揺れずに安定しているためには、車輪だけがその上下運動でうまく道路の凹凸に追従してくれればいい、そのためには質量は小さければ小さいほどいい、という理屈です。これはいかにももっともな議論といえます。
でもこれは四輪での話。それでは、二輪はどうかというと、同じ議論をコピーする例がほとんどですが、私はちょっと違います。
バイクの性能を簡潔に表すのに、よく「走る、曲がる、止まる」の標語が使われます。語呂がいいのでこれで定着していますが、正確には、「加速性能、旋回性、制動能力」というべきものでしょう。バイクが速いというのは最高速よりもその加速性能であり、また連続するカーブをひらりひらりと軽快に走り抜けることを指しています。そしてスピードをコントロールできるのはブレーキ性能があってこそです。
この3つの性能は、そのままサーキットでのレースで求められる性能とも言えます。レースで速いことが、そのままバイクが速いことを意味していました。
なるほど、バイクは速くなければつまらないものですが、なにもライダーみんながサーキットで競うわけではありません。のんびりと、あるいは高速道路をかっ飛ばして、遠出するのも楽しみ方のひとつです。いや、むしろ、ツーリングがバイクの楽しみの原点でもあるでしょう。かく言う私のバイクもレーサータイプではなくてツアラーモデルです。
そのナナハンツアラーで初めて高速を走ったときに、いままで400のCBXと250のXLRで走行したのとは違った感触がありました。それは、「曲がらない」こと。直進性が強くて、なかなか曲がってくれない印象を受けました。これはシャフトドライブのせいとは思えないし、ひょっとしたらホイールベースが長いためかしら。それ以来しょっちゅう高速を飛ばしていますが、どうも「直進性が強い」というより、なかなか寝かせられない、つまり「直立性」が強いことが分かりました。直立性も正確な言い回しではありません。高速カーブを曲がるとき、いちどリーンさせるとその傾きのまま安定して倒れるような不安が全くありません。「姿勢保持性」が強い、とでもいえばいいのでしょうか。
そうだとすると理由は明りょうです。ちょうどコマのように、車輪が回転することのモーメントが強く効いているんですね。ではそのモーメントの大きさはいかほどか？ 回転の慣性であるからには、タイヤは重いほうがいいのか？ ホイール径はどう効いてくるのか？
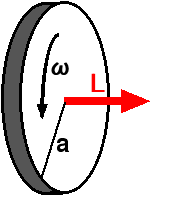簡単のために、かりに車輪をディスクのような一様な円盤とすると、その中心軸の回りに回転する車輪の慣性モーメント J は
J = Ma2/2 （Ｍはディスクの質量、aは半径）
となります。（もしも重量がリング状に円周付近に集中していたら J = Ma2 ）慣性モーメントは径の二乗に比例します。慣性モーメントとは、分かりやすくいうと、回転をかけるための手ごたえ、逆に回転を止めるための手ごたえの、その大きさ。慣性モーメント J のディスクが角速度 ω で回転するとき、その角運動量 Ｌ は回転軸の方向のベクトルで表されて、その大きさは
L = ωJ
この角運動量は、直線運動の運動量と同様、その方向と大きさを保とうとします。私のK75Sのタイヤサイズは、前輪が100/90-18、後輪130/90-17。
後輪を例にとると、ホイールの半径が17/2インチ、タイヤの太さが130mmで扁平率が90%ですから、厚みはおよそ130 x 0.9 = 117mm。したがって半径は0.33m。
車輪の重量はいかほどか。私は車の車輪は冬用と３シーズン用を交換するときに持ち運びしますが、二輪用の車輪はどのくらいの重量なのか知りません。ネットで検索しても、あれだけバネ下重量の議論は盛んなのに、実際にどれだけの重さなのか、ほとんど資料を見かけません。まあ、ここでは仮に10kgとしておきましょう。
このバイクで高速を走るとき、いつもは120キロで巡航するので、秒速にすると33m/s。タイヤの外周は0.66πmとなりますから、そのときのタイヤの回転数は16/s。角速度は 100/s。
車輪の重量配分がディスクみたいだと仮定すると、車輪の慣性モーメントは
J = 10 x 0.332/2 = 0.54
120キロ走行時の角運動量は
L = 100 x J = 54
これを、小径タイヤの典型であるスクーターと比べてみましょう。ホンダのFORZAのタイヤサイズは、前輪が110/90-13、後輪130/70-12。同様に後輪を例にとると、タイヤ半径 0.24m。重量は3割軽く、7kgと仮定してみましょうか。タイヤの外周が小さくなるので同じ120キロで走ると、回転数は 25/s。角速度は 157/s。すると、
J = 7 x 0.242/2 = 0.20
慣性モーメントは半分以下。同じ120キロで走行時の角運動量は、回転が増すので
L = 157 x J = 31
いろんな仮定の上での計算ではありますが、同じ速度で走っていても、これだけタイヤの回転による「直立安定性」が違います。たぶん、高速道路で急な横風を受けたときに、ふらつきの差が大きいと想像します。私が「曲がらない」と感じたのは、じつはこの寝かし込み性が鈍いせいでした。もちろん、トータルでは、ホイールベース、車重、重心位置、それにフェアリングによる整流効果なども効いてくるでしょう。ここで強調したいのは、二輪の場合は、バネ下重量はただ軽ければいいというものではないこと、たしかに回転の慣性モーメントが小さいほうが加速にも制動にも有利にはたらくが、タイヤの回転による角運動量はある程度必要なこと、もしもタイヤの重量（バネ下重量）がゼロだったら（したがって慣性モーメントがゼロなら）、高速走行時に直立姿勢を保つのは容易ではないだろうということ、私のようなツアラーには、クイックなハンドリングよりも、多少とも挙動が鈍いほうが長距離走行ではありがたい、ということ。
こういう違いは、バイクそれぞれの味なので、好みの問題ではもちろんあるでしょうが、それよりなにより、いろいろとタイヤを交換して走り比べる、ということはふつうしないので、こんな数字の議論もなかったのでしょう。いつかタイヤも靴と同じように、目的によって履き替えることが当たり前になったとしたら、きっとタイヤの重量と慣性モーメントの数字もカタログに載ることでしょう。二輪車の性能は、だから、「走る、曲がる、止まる、それと、倒れない」の４つ。