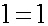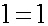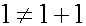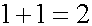数と人間

　数とは何かと問われると、ほとんどの人は答えに窮すると思います。この問題は、普段は話題に上りませんし、学校でもあまり教えられていません。ところが誰もが、数とは何かについて考えることなく、日常的に数を用いています。そこで、数とは何かを考えるには、数の使用方法について考えることからはじめます。数の素朴な使用方法として、一番最初に考え付くのは、具体的な物の個数を数えることです。そこで通常の大人が、日常生活で用いる物の個数を数えるてみます。数える対象としては、安い物の代表として新聞、高い物の代表として自動車について考えてみます。これらのものを数える場合、どこまでを1とするかを、はっきり決めなくてはいけません。それを厳密に考えると、非常に多くの問題があることに気づきます。例えば新聞を数える場合、通常はその日の朝刊全体をひとまとまりとします。ところが、その日に配られた新聞は当日しか価値がなく、翌日には古新聞と呼ばれ、紙としての価値しかなくなります。そうなると、通常は朝刊全体を1とは数えません。古新聞を物を包む紙として使う場合、新聞紙一枚を1とし、小さいものを包む場合などは、半分に切って一枚とする場合もあります。このように新聞または新聞紙を数える場合だけを考えても、どこまでを1とするかが難しいのです。今度は自動車について、どこまでを一台とするか考えて見ましょう。自動車は高価ですから、修理技術が非常に発達しています。自動車はぶつかると簡単にへこみますが、車体のへこみや傷は、かなりひどくても修理できます。例えば衝突などで、車体の前半分がつぶれた場合でも、自動車修理工場にもって行けば直してくれます。車体は重要ではなく、走ることこそが自動車の本質だ、という議論があるかもしれません。ところが自動車はガス欠でも走らなくなりますし、パンクしても、バッテリーが上がっても動かなくなります。その時に動かない自動車を見て、これは自動車ではないとは、誰も言わないでしょう。さらに自動車の心臓部に当たるエンジンが壊れた場合を考えてみます。古い車などでオーバーヒートしたりすれば、ラジエーターの水は沸騰し、エンジンは焼けてしまいます。最悪の場合であれば、エンジンを丸ごと取り替えなくてはいけません。ところがそうして修理すれば、自動車は再び走り出すのです。つまり、エンジン、車体、タイヤ、電気系統など、どこがやられても自動車は修理可能です。このように自動車はゾンビのような存在で、いくら壊れても再生可能なように見えます。そうすると、一台の自動車を1でなくする。すなわち廃車にするかどうかを、決定するのは持ち主しかありません。

　このように人間が作ったものについて、どこまでを1と数えるかは、最終的には持ち主が決定します。例えば新聞は一日で古新聞になりますが、持ち主が将棋が大好きな場合、将棋欄の名人戦には大きな価値があります。繰り返し読むために、切り抜いて保存する人もいます。次の例として、自動車を新車で買っても、十年もすると中古車としての価値も、ほとんどなくなります。それでも持ち主が大事に使えば乗り続けられます。さらに何十年もすれば、クラッシクカーとしての価値が発生します。この場合は、ほとんど走らなくても十分です。大抵の持ち主は、むしろ傷まないように、あまり外に出さないようにします。新聞および自動車の例では、どこまでを1とするかは人によって違い、主観的に決められていることが分かります。これら二つの例は人間が作った物ですので、そのせいで持ち主が勝手に1を決めてしまうのかもしれません。そこで自然のものである石を数えてみます。石の定義は広辞苑によると、岩より小さく、砂より大きい鉱物質のかたまりとあります。次に岩の定義を見ると、石の大きいものとあります。これでは大きいほうは流動的に決めるしかありません。せめて小さいほうだけ決めるために、砂の定義を調べてみます。砂の定義はアメリカとヨーロッパで異なりますが、どちらも粒径が2mm以下のものを砂としています。ところが普通の人は、それで納得するでしょうか。例えば男の子なら誰でも、石を投げて遊んだ経験はあると思います。そんな時、粒径1cm以下のものを、石として投げたりしなかったと思います。投げる場合は、必然的に石の大きさは決まってきます。そして男の子が石投げをする場合、投げるのに適当な大きさの石だけを1と数えます。ところが同じ石でも、お母さんが漬物石を数えるならば、投げるのは困難な重い石だけを1と数えます。このように自然物を数える場合でも、数える側の都合で何を1とするかは異なるのです。ここまでは生命のない物体のみを数えてきました。その場合は1は数える人の主観によって決定され、人によって違いが生じます。

　次に生命のあるもので、我々が最もよく知っている人間を、数えてみます。我々は人間を、大人でも子供でも、男性でも女性でも、一人と数えます。この場合は身長や体重のような大きさによる区別も、生まれてからの年数による区別もありません。さらに病気になったり、手や足がなくなったり、認知症になったりしても、一人の人間であることには変わりありません。このように、誰でも自分自身を一人と認識し、他の人間も一人と認識し、どちらも同じ人間と認識します。この認識を1の起源と考えます。次に人間を1として、自然数が構成できるかどうかを検討します。物の個数を数えるための数を、数学では自然数と呼びます。自然数は人間が最初に覚える数で、1,2,3,4…と順番に並んでいる数です。幼児は自然数しか使えませんし、エジプトとメソポタミアで文明が発生するまで、人類は自然数しか知りませんでした。その後に、ギリシャ人は数の性質を深く考え、現代につながる数学の基礎を作りました。プラトンは1の性質として、以下の二点をあげています。第一に1と1がお互いに等しいこと、第二に1が分割不能であることです。自然数を構成するために、もう一つの性質を付け加えます。第三に1と1を加えると2になることです。これらの三点について検討して、数式で表します。

　第一の点ですが、例えば石の場合、全く同じ組成で全く同じ形で、全く同じ重さの石が存在するとは思えません。厳密に考えれば、この世界に全く等しい物体はないと思われます。また、地球上に存在する全ての物体は、常に変化しており、一定の状態にあるのものはありません。岩石は常に風化しており、山や谷も地殻変動を受けます。どんな物体も、一定の状態を保つわけではありません。次に人間について考えてみます。人間を構成する細胞も、それを構成する物質も、常に変化しています。にもかかわらず、人間は自分自身を単一と認識します。この自己同一性を、新生児はすでに持っているように思われます。もちろん、まだ言葉がわかりませんから、大人と同じ意味ではありません。しかし、母親のおっぱいを求め乳を吸うには、多くの筋肉の協調が必要です。その意味で新生児は、すでに統一的行動がとれるのであり、自我の単一性があります。ところが統合失調症という病気では、自我が障害されるため、体が動かなくなる場合があります。筋肉の協調運動が障害されてしまうのです。このように自我の単一性は人間にとって重要であり、自分という個体を統一的に動かせなくてはいけません。このような自分を1とする認識を基盤に、大人は他の人間も同じ1として認識します。他人を一人とする認識は、遺伝子に組み込まれているに違いありません。脳には他の人間を認識するための特別なシステムとして、他の人間の顔を認識する顔細胞があり、他人の動作に反応するミラーニューロンもあります。おそらく他にも、他人を認識するための多くのシステムがあると思われます。このような自分と他人を、どちらも同じ一人とする認識を、数式で表すと以下のようになります。

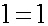
第二の点について、石を分割すれば二つの石になりますし、それ以上に分割することも可能です。またプラナリアは切断しても、それぞれの断片が完全な個体に再生します。それに対して、一人の人間を分割して二人になることはありません。人間の腕や足など一部を切断しても、切断された部分は単独では長期間の生存はできず、残った部分は一人の人間のままです。そして人間の胴体を無理に分割しようとすれば死んでしまいます。これを数式で表すと以下のようになります。

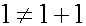
第三の点について、おにぎり二つをくっつければ一つになります。また粘菌などは細胞融合するので、二つの細胞が融合して一つの細胞になります。それに対して、二人の人間を結合して一人にすることは不可能です。二人を無理に外科的に結合しても、お互いに拒否反応が発生して、両者の生存が危なくなります。決して二人が融合して一人になることはありません。通常は一人と一人を近づけると、人と人が並んでいる状態になります。これをひとまとまりとして、二人と数えます。結局、1と1を加えると2になるので、数式で表します。

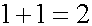
このように、1は加算しても不変ですので、逆に2は1と1に分けることが可能です。このように人間は、自然数を構成する1としての性質を持っています。何人かをまとめるということをすれば、自然数が構成できます。ここで、人間はまとめられても融合したり、陽電子と電子のように対消滅したりしないという点が重要です。人間は独立していて、簡単に変化しないので、まとめて数えられるのです。

目次｜次のページ