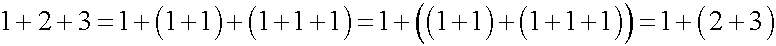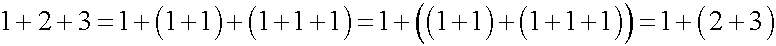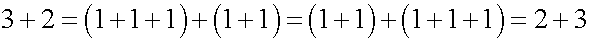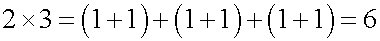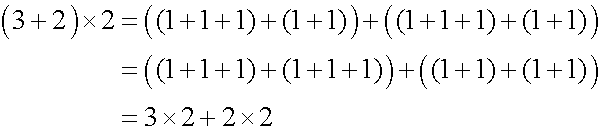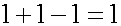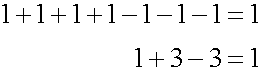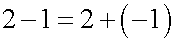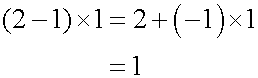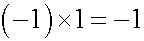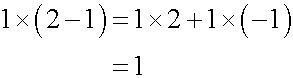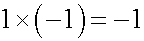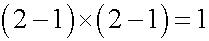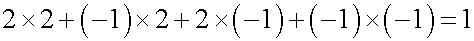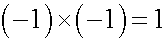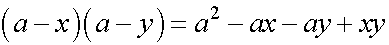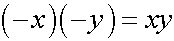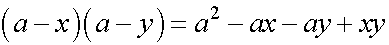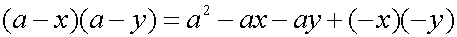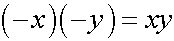マイナスかけるマイナスはなぜプラスか

　マイナスかけるマイナスがなぜプラスとなるかを考えるには、最初は自然数の足し算から始まります。人間は生後かなり早い段階から自然数の概念を持っていて、幼児でも数を数えられます。足し算もかなり早い時期から、指を使って可能になります。それは足し算は数えることの延長だからです。その後に引き算は苦労しますが、足し算の逆なので、何とか家で身につけることは可能です。ところが掛け算となると、学校なり塾なりで教えられない限りは出来ません。私自身も小学校では、九九の暗記に苦労した覚えがあります。暗記以外で掛け算は、出来るようにならないように思えます。自然数しか知らない段階では、掛け算は足し算の繰り返しと考えるしかありませんが、手の指は5本しかないので指を使っても簡単には出来ません。また歴史的に考えても、一般的に掛け算が行われたのは、四大文明の発生以後と思われます。つまり農耕の発明とともに土地の所有が生じ、土地の面積を計算するために、掛け算が一般化したと考えられます。それから数学が進歩し、少なくとも紀元前2000年頃の古代メソポタミアでは、マイナスかけるマイナスがプラスになることは知られていました。ここでは歴史に従って、はじめに自然数の足し算を導入し、足し算の結合則を導入します。次に足し算の繰り返しとして自然数の掛け算を導入し、分配法則を導きます。その後に負の数を導入し、自然数の引き算で分配法則が成立するには、マイナスXマイナス=プラスである必要があることを示します。その上で掛け算を面積と定義した場合も、同様にマイナスXマイナス=プラスであることを示します。なお、このページの簡略版として、マイナスかけるマイナスはなぜプラスかを作りましたので、時間のない方は簡略版の方を御覧下さい。

　自然数の足し算はどんな順序で行っても最後の答えは同じになりますが、それは物の個数を数える場合、どんな順番で数えても同じ数になることと同じ意味です。それを表す計算法則が結合法則です。結合法則は無条件に成立するとしなければ、数える順番によって物の個数が変わることになってしまいます。

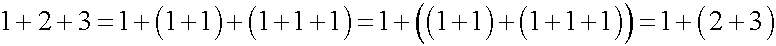
足し算の交換法則は結合法則から導けます。

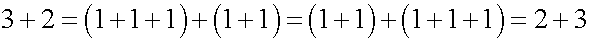
ここで掛け算を導入します。

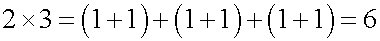
このように掛け算は足し算の繰り返しとして導入されます。そうすれば必然的に掛け算でも、交換法則、結合法則が成り立ちます。次に分配法則は、足し算の結合法則から導けます。

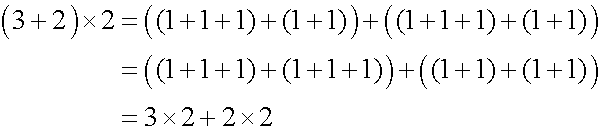
　分配法則まで準備してから負の数を導入します。ところが、負の数の導入は歴史的には困難を極めていて、先人達はなかなか納得できずに悩んだようです。パスカルなども負の数の存在は認めていなかったようです。負の数を初めて本格的に導入したのはデカルトですが、パスカルのパンセにはデカルト悪口がたくさん書いてあるし、「私は0から４を引けば、0であることの分からぬ人を知っている。」とも記載してあるぐらいです。パスカルですら受け入れにくいのですから、安易に負の数を扱うべきではありません。

　しかし、現代ではあまりにも簡単に負の数を用いていて、自明のことと考える人が多くなっています。それは、水の凝固点を便宜上0度と決めた事によって、それ以下の温度にマイナスを用いてしまったのが大きいのかもしれません。現行の0度には物理的必然性は無く、本来は絶対零度である-273度を0度とすべきであって、現に熱力学ではそうしています。そうすると0度より低い温度はあり得ないことになります。その時点でいくら冷却しても無駄なので、パスカルの言い分が正しいことになります。他にも海抜0メートル地点よりも低い地点をマイナスとしますが、これも便宜上の0です。物理的には地球の中心点を0とするべきで、それより低い地点は存在しません。これは時間についても同じで、キリストの生誕後を紀元後、生誕前を紀元前としていますが、物理的にはビッグバンの時点を0年0時0分0秒とするべきで、現代物理学によるとビッグバン以前に時間は存在しません。この便宜上のゼロという考え方が、マイナスについての誤解の原因となっています。ここで便宜上の0と物理的な0の違いを示す例を考えます。野球をするには最低9人の選手が必要なので、通常は野球チームは9人より多い人数で構成されますが、草野球チームの中には選手の数がぎりぎりのチームもあります。そのチームの選手のうちの一人でも急な仕事が入ったり体調が悪かったりすると、そのチームは選手が足りなくなってしまいます。そこで9人に対して余った人数をプラスで、足りない人数をマイナスで表すとします。この表し方は人数の過不足を一目でわかる方法で、9を便宜上の0とします。それによって選手を貸し借りすることも出来て、選手の足りないチームでもゲームが出来ます。例えば10人のチームは+1人、15人のチームであれば+6人となりますが、10人のチームでも3人が欠場すれば-2人となります。ところが、あるチームが選手を貸しすぎて-9人になった場合は、そのチームには選手がいませんので、そのチームから選手を借りることは出来なくなります。選手を4人借りたいと頼んでも断られるだけです。ここで-9を物理的な0に戻すと、パスカルの言うように、0から4を引いても0です。

　もう一つの例を挙げて、物理的な0には多くの種類があるということを述べます。例えば100人乗りの飛行機があったとします。乗客が1人もいない場合は0になりますが、これには多くの例が考えられます。まず乗客がおらず飛行機の座席が100席空いている場合、これを通常の0と考えます。次に飛行機が墜落した場合、これは単なる0ではなく大変な事態です。それでも代わりの飛行機を補充できれば、通常の0として扱って問題ありません。ところが離島の場合、飛行機が墜落しなくても、飛行場が自然災害で被害を受けて使えなくなったとします。こうなると0は全く違う意味になります。この場合の0は飛行機が離着陸出来ない状態なので、座席の予約すら出来ません。これを異常な0とすると、異常な0に数を足すことは無意味です。同じ物理的な0でも、通常の0と異常な0では全く意味が違います。しかも座席が予約できない異常な0には、他にも色々な場合があります。航空会社が倒産することもあり得ますし、最悪の場合は戦争ということもあり得ます。

　便宜上の0と物理的な0の違いに対する理解の不足が、最近増加している借金地獄の原因ではないかと考えられます。伝統的には借金をマイナスとする考え方がありますが、それが成立するのはやはり便宜上の0の場合です。借金には担保も必要であり利息も付き、支払期限もあるのが普通であり、本来返却を前提とします。やはり実体はプラスであり、ただ手持ちの現金が無いという便宜上の0でなければ借金をマイナスとは考えられません。物理的な0である完全な無一文では、誰もお金は貸してくれません。このように便宜上の0は誤解の元になり、抽象思考に慣れていないと危険です。そのため最初は計算の途中に0やマイナスが出てこないようにして、引き算を足し算の逆の操作として導入します。1に1を足すと2になりますが、そこから1を引くと1に戻ります。つまり、1を足すことの逆を1を引くこととします。

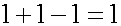
これを何回繰り返しても同じとすると、任意の数について足し算の逆は引き算となります。

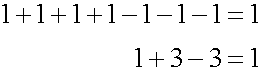
ここで負の数を導入しますが、負の数を足すことは正の数を引くことと同じと定義します。すなわち-1を足すことと1を引くことが同じとなります。

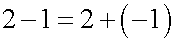
このように負の数を定義した上で、自然数の引き算にも分配法則が適用できるように、負の数の掛け算の計算法則を定義します。そのために例を用いますが、自然数は物の数を数えるために用いるのが基本的な使用法です。そこで具体的な例として、皿の上に乗ったお菓子の数を数えます。最初に1枚の皿に2個のお菓子が乗っているとします。そこから1個のお菓子を取り除くとお菓子の数は1個になるので、数式で表します。

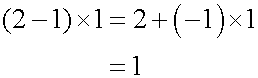
左辺は (1皿あたりのお菓子の個数)X(皿の枚数) という式になっていますので、右辺は必然的にお菓子の個数になります。右辺の2は最初のお菓子の個数を表します。そこから1個のお菓子を取り除くので、1を引くことになります。すなわち後の(-1)X1は-1に等しくなるので、マイナスかけるプラスはマイナスとなります。

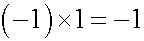
次にプラスかけるマイナスはマイナスを導きます。今度は1個のお菓子が乗った皿が2枚あったとします。1枚の皿を取り除くと、お菓子の数は1個になるので、数式で表します。

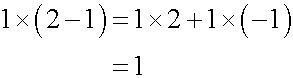
前の式と同じように考えて、やはり1個のお菓子を取り除いたことになるので、プラスかけるマイナスはマイナスとなります。

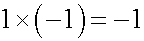
最後にマイナスかけるマイナスはプラスを導くために、まずは現実の例で考えてみます。私に弟と妹がいるとして、3人でお菓子を分けて妹の取り分が何個になるかを考えます。2の皿に2個ずつのお菓子がのっているとします。この状態を数式で表すと 2X2=4 となり、お菓子は全部で4個です。前の2は1皿あたりのお菓子の数を表し、後の2は皿の数を表すとします。私は兄の特権として、それぞれの皿からお菓子を、先に1個ずつ食べたとします。この状態を数式で表すと、(2-1)X2=2 となり、お菓子は全部で2個で、１つの皿に１つのお菓子がのっている状態になります。そこで初めて弟と妹を呼び、平等に弟と妹に1皿ずつ分けたとします。妹の取り分は1個となり、数式で表すと (2-1)X(2-1)=1 となります。この式は括弧の中を先に計算すると、左辺と右辺が等しいのは自明です。

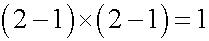
左辺に分配法則を適用します。

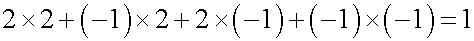
左辺を整理すると、マイナスかけるマイナスはプラスとなります。

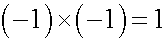
このよう負の数の計算規則を定めると、自然数の引き算に分配法則が適用出来ます。この段階までは、掛け算は足し算の繰り返しとする定義を用いました。離散的な量を扱うにはこの定義で十分ですが、それでは連続量は扱えません。ところが掛け算には面積を表すという重要な意味があり、掛け算が面積を表すと定義すれば連続量を扱えます。そこから無理数という概念が生じました。また面積の概念から積分へとつながります。

　次に掛け算を面積として定義し、図を用いて説明します。穀物生産のための農地の面積を計算しますが、米の場合であれば一定の間隔で一列に稲が植えられます。そのため一本の稲に必要な面積を単位正方形として、面積は単位正方形の個数で計算するのが便利です。結果的に2X3=6という式は、下の図のようになります。

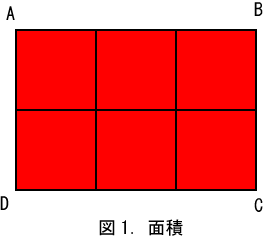
それを図2に、(3+2)X2=3X2+2X2=10 という式を示します。長方形ABCDの面積を計算する場合、底辺DCの長さを出して高さを掛けても、赤色の長方形と黄色の正方形の面積をそれぞれに計算してから足しても、どちらも答えは10になります。

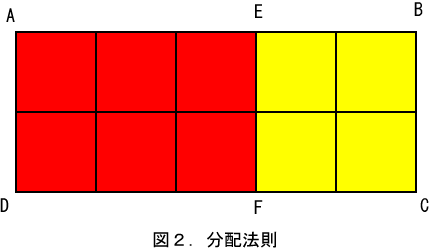
(2-1)X(2-1)=1 を図示すると図3となります。1辺の長さが1の正方形を単位正方形と呼びます。正方形ABCDは4個の単位正方形から成るので、正方形ABCDの面積は4となります。この式は正方形ABCDの各辺の長さを1短くするという意味ですから、前の項と後の項で、それぞれ赤の部分の2個の単位正方形を取り除くことになります。ところが単位正方形EBFJは2回数えられているので、結果的には3個の単位正方形を取り除いたことになります。最終的には一番右の図の黄色の単位正方形が残るので、答えは1となります。

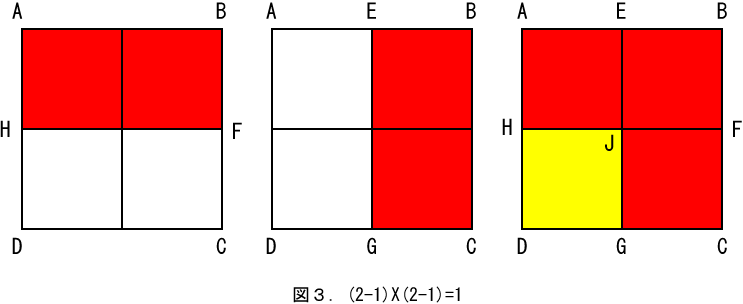
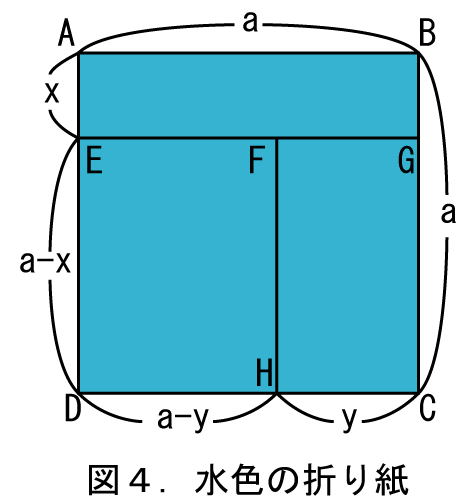
次に一般的な図形を用いる方法については、今までに色々と考えられて発表されています。小さな工夫として、私は折り紙を用いる方法を二種類考えました。1辺の長さaの水色と黄色の折り紙を、それぞれ1枚用意します。最初に水色の折り紙に下の図4のように線を引きます。次に線分EGに沿って折り紙を切り、水色の長方形ABGEを得ます。さらに線分FHに沿って折り紙を切り、水色の長方形FGCHを得ます。残った水色の長方形EFHDは使いませんので捨てます。

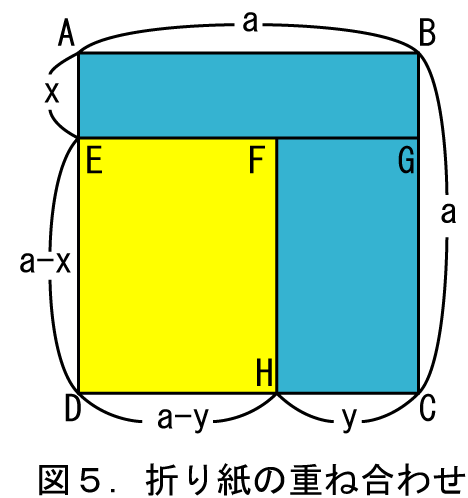
次に黄色の折り紙の上に、さきほどの二枚の水色の長方形の折り紙を図5のように重ね合わせます。そうすると下にある黄色の折り紙が見えている部分、すなわち黄色の長方形EFHDの面積は(a-x)(a-y)となります。

次に水色の長方形FGCHを、下の図6の長方形EF'G'C'と一致するように移動します。こうして線分C'G'を延長すると、線分BCと直交しますので、交点をLとします。

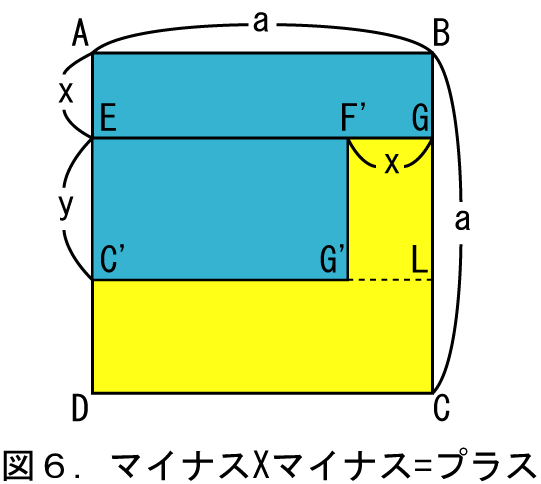
ここで下にある黄色の折り紙が見えている部分の面積を求めます。まず長方形C'LCDの面積は、図6から明らかなように、全体の面積から長方形ABGEと長方形EGLC'を除いたa²-ax-ayとなります。次に長方形F'GLC'の面積はxyとなります。これらを合わせた黄色の部分の面積は、図4の長方形EFDHと一致します。そこから以下の式が成り立ちます。

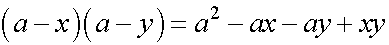
左辺を展開して整理します。

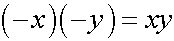
このようにして折り紙を用いて、マイナスかけるマイナスはプラスが導けました。蛇足かも知れませんが、もう一つ別の方法を示します。1辺の長さaの水色の折り紙2枚と黄色の折り紙1枚を用意します。1枚の水色の折り紙から、長辺の長さaで短辺の長さxとyの2つの長方形を切り取ります。合計4個の長方形を図7のように並べて、下から黄色の折り紙が見えるようにします。

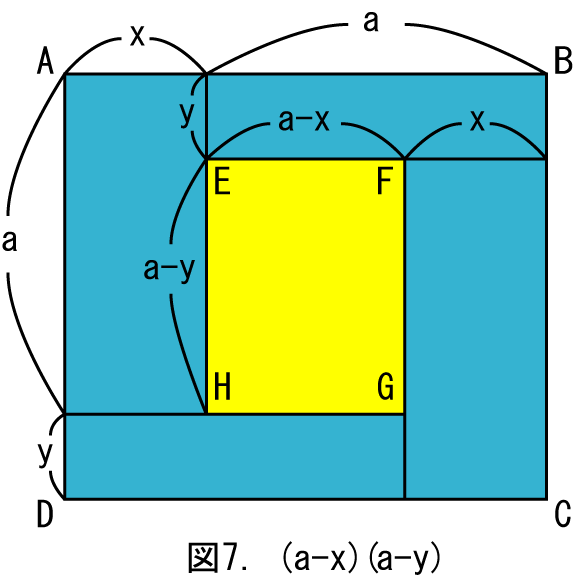
図7において、黄色の長方形EFGHの面積は(a-x)(a-y)となります。次に4つの長方形を図8のように並べ替えて、図形的に黄色の部分の面積を求めます。黄色の折り紙は図にあわせて切り取ります。

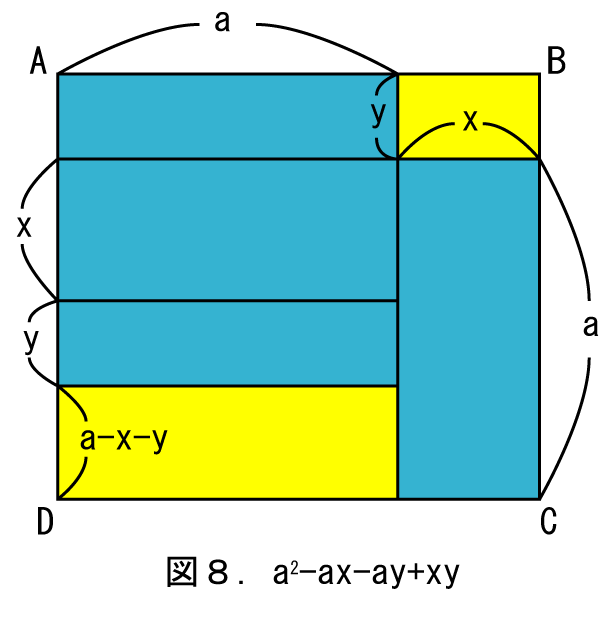
右上の黄色の長方形の面積はxy、左下の黄色の長方形の面積はa²-ax-ayとなります。これらの黄色の2個の長方形の面積を合計すると長方形EFGHの面積と等しくなり、結果として以下の数式が成り立ちます。

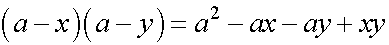
(a-x)(a-y)を分配法則を用いて展開します。

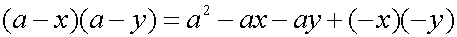
両者の結果を比較すると、以下の式が成り立ちます。

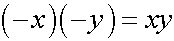
このように図形的にもマイナスかけるマイナスは導けますし、その方法はこれ以外にもあります。学生に新しい方法を考えさせるのも良いと思います。これらの方法が学力低下防止に寄与することを望みます。学校の先生でこのページを見られた方がありましたら、是非教育に用いて欲しいと願っています。

　このページでは、正の数の引き算に対して分配法則を適用出来るように、負の数の計算法則を定めました。本格的に負の数を導入しなくても、引き算と掛け算だけで負の数の計算法則は必要になります。現実の世界に真の負の数は存在しない、または非常に特殊な状況でしか有り得ないでしょう。もっとも一般的なのは借金でしょうが、誰もが投資する場合は何らかの見返りを求めます。例えば有名なインターネット企業のアマゾンなどは当初は借金ばかりでしたが、投資家はそのアイデアの可能性に賭けたのです。仮にアイデアを資産と考えれば、必ずしも赤字ではなかったのかも知れません。　ところがアイデアの値段は計算しにくいので、会社の収支を計算する場合などは、やはり負の数があった方が便利と思われます。

　ここまでは、負の数が現実には存在しないことを重視しましたが、現実的には負の数を用いた方が便利な場合もあります。例えば－273度を0にしてしまえば、20度ぐらいの温度も293度と言わなければならず、人間の生活にとって重要な水の凝固点も273度となって、日常生活では使いにくいのです。この場合は便宜上の0である水の凝固点を0度としたほうが、絶対0度を用いるよりは遙かに便利です。そう考えると、この段階までは計算の途中での負の数のしか認めませんでしたが、ここまでの内容を十分に理解した生徒には、単独での負の数の使用を認めても良いと思います。ただ負の数は数学の世界の中にだけしか存在しないということを理解していることが前提です。そのあたりの教授方法については、今後検討していきたいと考えています。

前のページ｜目次｜次のページ