次に、0から1までの数直線を、長さdの線分と長さ(1-d)の線分に、切断する場合を考えます。この場合は、0とdの間とdと1の間の両方について、それぞれ最低2個ずつの有理数が存在しなくてはいけません。カントールによると、長さdの線分上には、0から1までの数直線上と同数の点が存在します。そうすると、長さdの線分を切断する操作は、長さ1の数直線を切断する操作と同型となります。そう考えると、切断を作る操作は常に同型の操作の繰り返しとなり、永遠に終わらないのです。この操作は常に2個以上の有理数を生成すると考えられるので、長さ1の数直線をn回切断すると、最低2(n+1)個の有理数を生成します。つまり切断を生成すると、どうしても有理数を生成してしまうのです。
こう考えるとn個の切断に対して、最低2(n+1)個の有理数が存在するということが解ります。そうすると、有理数が可算無限個であるのに、無理数が非可算無限個であるというのは整合性がとれません。どう考えても、無理数による切断と無理数による切断の間には、最低二つの有理数が必要です。そう考えると無理数は可算無限個しかないことになります。それを切断を表現する表を用いて考察します。
最初に数直線上に有理数は最初から存在しているのではなく、切断によって生じるということが前提となります。正の有理数を自然数の組み合わせとして、縦の列では分母を1ずつ増加させ、横の行では分子を1ずつ増加させて、有理数を1個ずつ作成していきます。これは一般の有理数m/nに対して、nを1から始めて限りなく増加させる操作と、mについても限りなく増加させるという二つの操作を行うことを意味します。分母を増加させていくと0に収束し、分子を増加させると無限大に発散します。
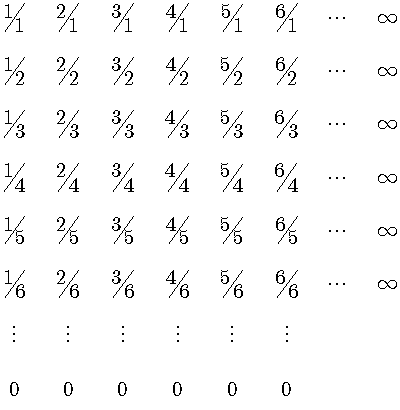
次に正の有理数を(0,1/2]と(1/2,∞)の二つの区間に分けた表を示します。(0,1/2]の表の境界線の列は、偶数項は1/2で、奇数項は分子をnとすると一般項はn/(2n+1)となり、どちらも極限値を取ると1/2に収束します。(1/2,∞)の表の方は、各行の極限値を取ると、どの行も単調増加数列なので無限大に発散します。この表の境界線の列の一般項は、奇数項は分子をnとすると一般項はn/(2n-1)となり、偶数項は分母を2nとすると一般項は(n+1)/2nとなり、どちらも極限値を取ると1/2に収束します。
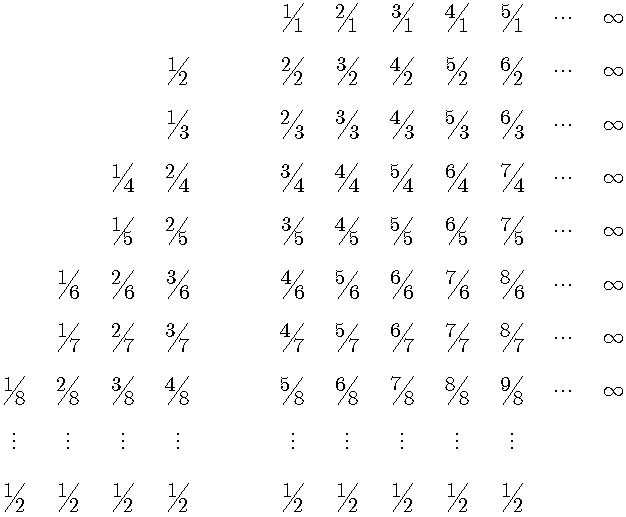
このようにして有理数の切断を表に示すことが出来ます。分母および分子がn以下の有理数の総数はn2となり、そのうち既約分数の比率の極限値は6/π2となり、nを限りなく増加させると既約分数の数は6n2/π2に近づきます。これは明らかに可算無限個です。この既約分数を大きさの順に並べると、切断は既約分数を2つに分けます。ここで無理数による切断は、必ず既約分数と既約分数の間に入るので、既約分数の数を超えません。ここで既約分数の数を限りなく増加させても、無理数による切断が可能な場所は既約分数の数を超えないので、必ず可算無限個になります。 次に同様の考察を小数に関しても行うために、小数を同様の表に並べてみます。正の小数を分数m/10nの形で表します。縦の列では分母10nのnを1ずつ増加させて、横の行では分子mを1ずつ増加させます。横の行では分子が限りなく増加するので無限大に発散し、縦の列では分母が無限大に増加するので0に収束します。
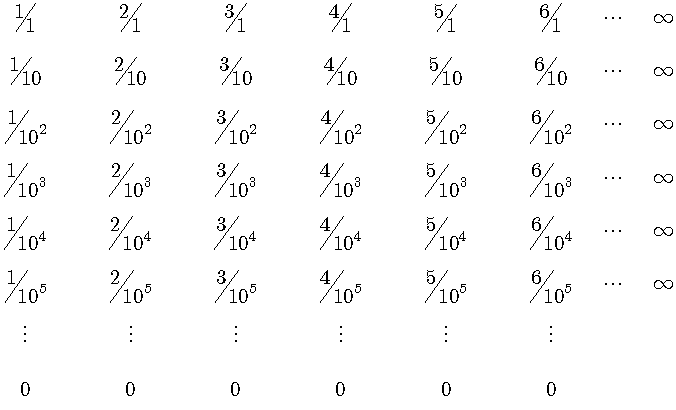
次に正の小数を(0,√2)と(√2,∞)の二つの区間に分けた表を示します。(0,√2)の表の各列は、上限が√2の単調増加数列なので、極限を取ると√2に収束します。(√2,∞)の表の方は、各行の極限値を取ると、どの行も単調増加数列なので無限大に発散します。またどの列も下限が√2の単調減少数列なので、極限を取ると√2に収束します。
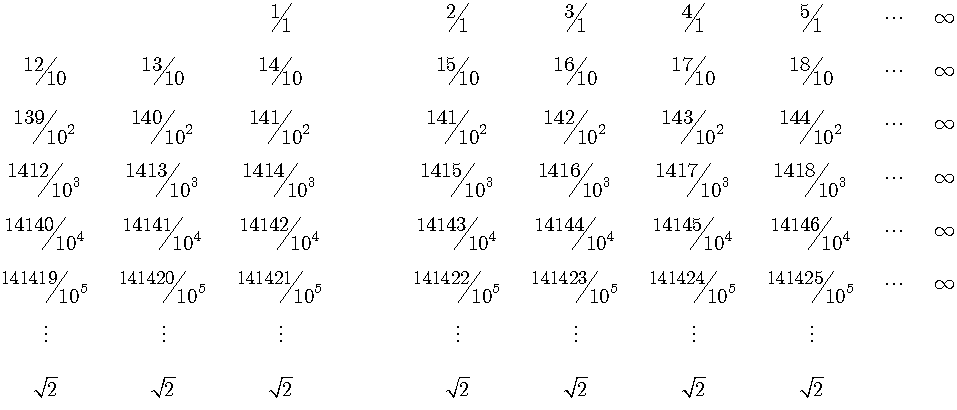
この表を用いることによって、小数の表の切断として実数を表すとが出来ます。