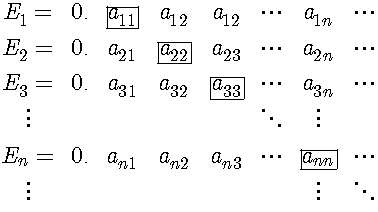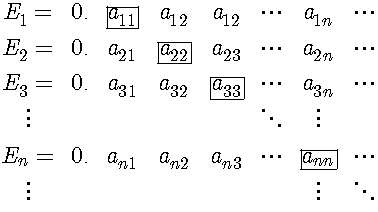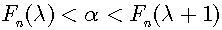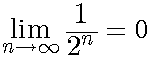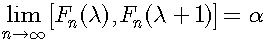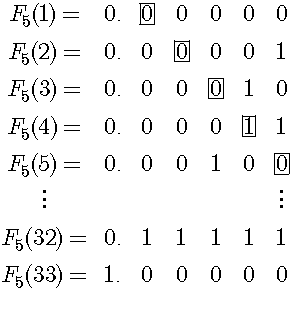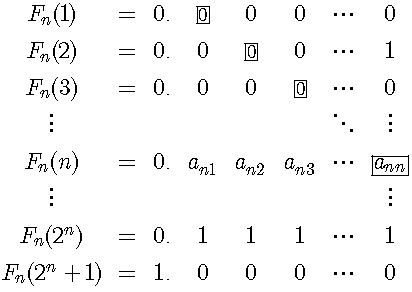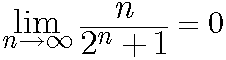対角線論法について
神経科学の立場で無限を考える場合、アリストテレスの可能無限は相性が良く、このホームページでは可能無限の立場で、無限をループと考えて議論を行った。それに対して、現代数学で主流となっているのは、Cantorの実無限の立場である(1)。Cantorは無限の濃度を分類したが、その時に中心的な役割を果たすのは対角線論法である。ところが対角線論法はあくまでも実無限を前提とした論法であり、可能無限を前提とすれば対角線論法は成立しないことを示す。
まず無限の濃度として、自然数と1対1の対応がつく場合を可算無限という(2)。それに対してCantorは、実数は自然数と1対1の対応がつかず、非可算無限であると述べている。Cantorが最初に対角線論法を用いた論文の英訳(3)では、抽象化して2種類の文字の列について述べている。同様の議論をするために、0から1までの区間の実数を二進無限小数で表し、その全てに自然数によって番号が付けられたと仮定し、n番目の数をEnと表し、Enの小数点以下m桁目の数をanmで表し、番号順に並べると以下の表になる。ここで注意すべきは無限小数は現実に無限の桁が存在し、それが表に並んでいる。同様に、全ての無限小数を並べ終えた状態が表になっている。つまり実無限が成立した状態を想像する。
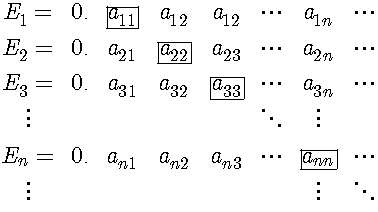
ここで四角で囲んだ対角線上にある数、a11と異なる数b1というふうに、それぞれの対角線上の数annと異なる数bnから小数以下の各桁が構成される無限小数B=0.b1b2・・・bn・・・を考えると、この数は上の表に含まれるm番目の無限小数amとm桁目の数とが必ず異なっており、表のどこにも含まれない。このように必ず表に含まれない数が存在する。そのため、0から1までの区間の全ての実数に番号を付けることは不可能であり、実数は非可算無限であるというのがCantorの主張である。ここで注意点として、Cantorの原論文では二種類の文字を用いているが、0から1までの区間の無限二進小数とすると、小数点以下の0と1のあらゆる組み合わせが含まれるので、二種類の文字のあらゆる組み合わせと同等になる。なお注意点として0=0.00・・・となり、また1=0.111・・・となり、0と1は表に含まれる。
神経科学の立場としては、実無限を認められないので、可能無限の立場から対角線論法について考察する。最初に、小数点以下n桁の有限二進小数で無理量を近似する方法について考察する。0以上1以下の小数点以下n桁の全ての二進小数を、小さい順に並べた表をT(n)と名付ける。なおT(n)には0と1を含める。ここでnを可変とすると、任意の桁数の二進小数の表が作成可能である。この表を用いて二進小数で表せない数を近似していく。二進小数であらわせない0以上1以下の任意の実数をαとして、表の各二進小数と大きさを比較する。λ番目の小数点以下n桁の二進小数をFn(λ)と表すと、以下の式を満たすλが必ず一つ存在する。
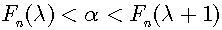
この場合にFn(λ)をαの近似値とする。その上でT(n)においてnを限りなく増加させた場合、Fn(λ)とαとの誤差d=1/2nは限りなく0に近づく。ε-δ論法を用いると、任意の正の数εに対して、ある適当な自然数Nが存在し、Nより大きい全ての自然数nについて1/2n<εが成り立つ。これを極限で表現すると以下のようになる。
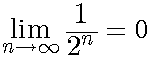
極限まで近似を行えば誤差が0になるということは、Fn(λ)とFn(λ+1)の組による閉区間[Fn(λ),Fn(λ+1)]に区間縮小法を用いると、実数αによる切断が得られる。
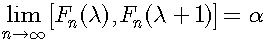
このように0から1までの区間の、あらゆる実数は表T(n)を用いて任意の精度まで近似できる。さらに極限をとれば、任意の実数の切断を得ることが出来て、実数の切断は無限小数として極限の表に表示することが出来る。そして有限の範囲では、対角線論法はnxnの表でしか適用できない。それに対して、小数点以下n桁の有限小数をすべて含む表はnx2nとなるので、対角線と異なる数を作成しても、表にない数を作ることは出来ない。さらに有限小数の桁数が増えるに従って、対角線数によってカバーできる有限小数の割合が減少するということを以下に示す。まず、0以上1以下の全ての5桁の二進有限小数について、小さい数から順に0を省略せずに並べて表に示す。ここでF5(n)はn番目の5桁の二進有限小数を表す。
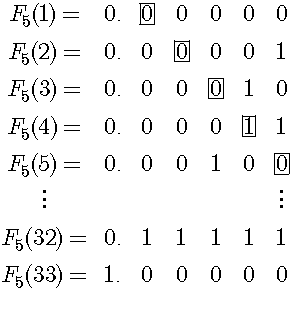
この時に四角で囲んだ対角線上にある数を考える。ここで、小数点以下5桁の小数に対する対角線は5番目までの数しかカバーしない。ところが0以上1以下の小数点以下5桁の二進有限小数は全部で33個あるという点に注意が必要である。図において四角で囲んだ数を並べて小数を作るとF5(3)=0.00010となり、表の上から3番目の数と一致する。これと小数点以下の全ての桁が異なる小数はF5(30)=0.11101となり、表の下から4番目の数と一致する。このように5桁の有限小数を全て含む表では対角線論法は適用できない。次に小数点以下n桁の場合を考察する。そこで0以上1以下の全ての小数点以下n桁の二進有限小数を、小さい数から順に0を省略せずに並べて表に示す。
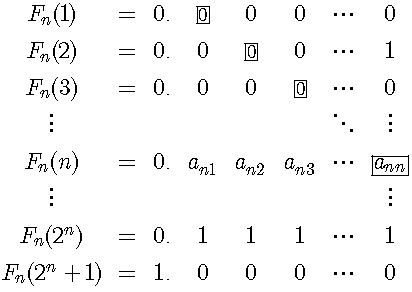
上の表で、Fn(m)は小さい方からm番目の小数点以下n桁の二進有限小数を表す。ここで対角線上の四角で囲んだ数a11・・・annと、異なる数b1・・・bnから小数以下の各桁が構成される有限小数B=0.b1・・・bnを考える。この場合、Bは0以上1以下の小数点以下n桁の二進有限小数であるので、必ず表に含まれる。次にこの表において、対角線がカバーする二進小数の数nの、0以上1以下の小数点以下n桁の二進小数の総数(2n+1)に占める割合について考察する。nを増加させると、この値は急激に減少して0に収束する。
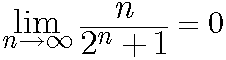
ここで具体的にT(150)、すなわち小数点以下150桁の場合を考えてみる。表の行数は約1.4x1045となる。この数字には実感がわかないが、宇宙の大きさは大きく見積もっても1030m程度と考えられており、陽子の大きさが10-15m程度とされるので、その比は1045ぐらいである。表の高さを宇宙の範囲内に収めるには、陽子1個につき1個の数字を表すようにしても、陽子を宇宙の端から端まで隙間無く並べる必要がある。それに対して表の横幅は、小数点を1桁として全桁数は152なので、隙間無く陽子を並べれば陽子152個分の長さとなり、水素原子より遙かに小さい。そして対角線数がカバーできる範囲は150行までである。このように対角線がカバーする二進小数の個数nの表全体に占める割合は、nを限りなく増加させると0に限りなく近づく。
参考文献
1. J. W. Dauben, Georg Cantor, Princeton University Press(1990)
2. 森毅:無限集合,共立出版(1976)
3. S. Lavine, Understanding the Infinite, Harvard University Press(1998)
前のページ | 目次 | 次のページ