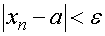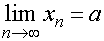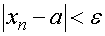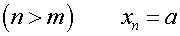数と量の関係
実数とは何かにおいては小数の切断として無理数を定義したが、これはあくまでも架空のユークリッド空間での議論である。現実とユークリッド空間の間の入出力は必ず離散的な活動電位が単位となる。視覚を例に取ると、網膜の光受容体が光子を単位とした光電効果に基づく反応しかできない。光受容分子である11-cis retinalは、一個の光子によって励起され、たった10-12秒でall-trans retinalに異性化される(1)。これは明らかにデジタル的な反応である。つまり外界からの画像入力は、生データとしてはビットマップ画像となり、網膜の解像度によって最小の長さが存在する。また脊髄のα運動ニューロンは、デジタル的に筋肉の運動単位を支配しているので、我々の描く絵も原理的にはビットマップ画像となる。つまり人間の入力も出力もデジタルなので、必然的に長さは最小の長さの整数倍となる。そうすると世界自体はどうあれ、人間が認識するのは神経細胞の活動電位に基づいたデジタルの世界しかない。ところがデジタル信号を元に、大脳は連続的なユークリッド空間を創作する。そこには円及び直角二等辺三角形が実在する。このユークリッド空間と現実の関係を下に大まかな模式図として示した。
現実→入力→感覚器→離散的信号→大脳皮質感覚領域→大脳皮質連合野→(ユークリッド空間)
現実←出力←運動器←離散的信号←大脳皮質運動領域←大脳皮質連合野←(ユークリッド空間)
上に示したように、感覚入力はすべて離散的な活動電位として大脳に入る。例として体性感覚には、温覚、痛覚、触覚、その他多くの種類の感覚があり、それぞれ特有の感覚受容器がある(2)。それぞれに対応した神経細胞の活動電位は、脊髄後角の神経細胞に送られ、視庄を経て大脳皮質の体性感覚野に送られる。一般的に感覚入力は感覚器で離散的な活動電位に変換され、感覚神経を通じて大脳皮質の感覚領域に到達する。これは各種の感覚で共通であり、視覚も聴覚も嗅覚も味覚や体性感覚もすべて同様である。次に各領域から情報は連合野に送られる。連合野には自分の体を中心にしたユークリッド空間が形成されており、全てのものは空間内に配置される。例えば音であれば、音源の方向と距離が特定され、ユークリッド空間内の位置が決定される。臭いであっても同様に、臭いの源の位置が決定される。このように人間の認識はユークリッド空間を舞台として行われる。そしてユークリッド空間内で、連続についてで述べたように、ニュートン力学に基づいたシミュレーションが行われる。その結果は大脳皮質の運動野に送られ、運動神経を通じて離散的な活動電位として、脊髄のα運動ニューロンを経て筋肉に出力される。このように人間の神経系は入出力に関してはデジタルである。そのため脳から見れば、ピタゴラスのいうように世界は数から出来ている。
この原理を視覚に当てはめると、視野は画素から出来ており、画素の大きさとしての最小の長さが存在する。人間の眼の解像度は、個人差はあっても大体0.1mmまでであり、そのあたりが何も機器を用いない場合の最短の長さとなる。それを虫眼鏡や顕微鏡で拡大するのであるが、可視光線の範囲でいくら拡大しても光学顕微鏡で1000倍程度が最高である。その場合で最短の長さは0.1μ程度となる。次に機器による測定について考えた場合にも、どうしても測定誤差というものが存在する。そのため一定の長さ以下は無視することになり、どうしても最短の長さに近い考え方が必要である。天文学、地質学、生物学、化学など、科学の様々の分野で、状況に応じて最短の長さは決定されている。これが建築や工学などの実用分野になると、精度が高すぎても良くない状況まで生じてくる。建物や機械の設計などでは、安全性に問題がなければ、コストパフォーマンスによって精度は決定される。次に歴史的に考察してみると、おそらく古代においては肉眼による解像度の限界のため、最短の長さdの限界は固定していたと考えられるが、近代科学の進歩で変化させることが可能となった。肉眼での解像度は0.1mm程度であるが、電子顕微鏡ではの分解能は0.3nmまで可能であり、ほぼ原子の精度である。このように最短の長さは、歴史的にも実用的にも可変であり、必要に応じて選択される。
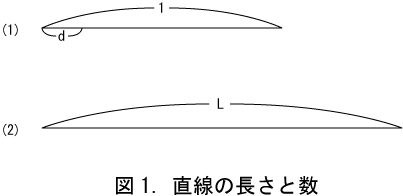
現実の空間で図形を扱う場合、最短の長さの整数倍のみを数とすれば、図形をビットマップとして扱える。ここでは無理量を数によって近似する方法について考察する。 図1の(1)に単位となる線分の長さを1として示した(3)。実用的には最短の分割不能な長さが存在すると考えて良いので、dは最短の長さとして示す。次に図1の(2)において一般の線分の長さをLとして示した。必然的に任意の長さLはdの整数倍となり、単位となる線分との間に整数比を持つはずである。このように現実の世界ではd未満の長さは無視される。それを図示したのが下図である。
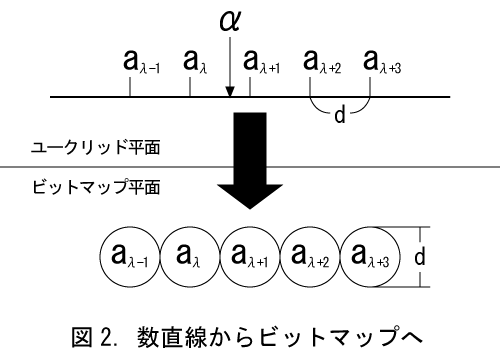
図の上側にはユークリッド平面上の数直線を示した。dは実用上の最短の長さを表し、aλ,aλ+1などの目盛りは小数を表し、αは無理数を表す。ビットマップ平面は現実に近い世界であり、最短の長さ以下の長さは存在しない。aλ,aλ+1などの直径dの円はドットを表す。ここでユークリッド平面にαという無理数があっても、一番近い小数であるaλ+1に近似される。これを実例を挙げて説明する。ここで最短の長さdを肉眼の分解能である0.1mmとし1mを基準となる長さとする。そうするとaλは、小数点以下4桁の小数となる。ここでαを2の平方根とすると、αは小数点以下4桁の有限小数で近似されてα=1.4142となる。等しい二辺の長さが1.0000mで、斜辺の長さが1.4142mの擬似直角二等辺三角形を作図したとすると、人間の目には直角二等辺三角形そのものにしか見えない。ただし、ここまでの精度は製図の玄人しか達成できないし、普通の人は必要としない。素人である我々の場合、1cmを基準の長さとし1mm未満の長さを無視して、長さを小数点以下1桁の有限小数で近似して、α=1.41として十分である。そうして斜辺の長さが14.1cmで、等しい二辺の長さが10.0cmの擬似直角二等辺三角形を作図しても、普通は直角二等辺三角形にしか見えない。このようにd未満の長さを無視しても、実用上は何の不自由も生じない。
人間がうまく行動するには、最短の長さのあるビットマップ空間と、最短の長さのないユークリッド空間を相互に変換する必要がある。そのためユークリッド空間とビットマップ空間の両方に適用可能な、ワイエルシュトラスのε-δ論法を用いて、数列の収束を考察する。最初にユークリッド空間における数列の収束を、ε-δ論法を用いて記載する。
数列xnにおいて、任意の正の数εに対して、適当な番号mを決めると、n>mのすべてのnについて、
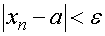
となるならば、以下の記号で表す。
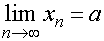
この場合、数列xnはaに収束するという。また、aを数列xnの極限値という。
これがユークリッド空間におけるε-δ論法(4)であり、実数の範囲での収束の定義となっている。ここでaは、実数についてで述べた有理数の切断すなわち実数を表し、幾何学的には数直線上の一点を表す。
次に最短の長さdのあるビットマップ空間におけるε-δ論法を以下に記載する。その場合は最短の長さdによって有効数字が決定され、aもXnも有限小数で表される。
数列xnにおいて、任意の正の数εに対して、適当な番号mを決めると、n>mのすべてのnについて、
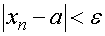
となる場合、ε<dとなるようにεを決めれば、n>mのすべてのnについて以下の式が成立する。
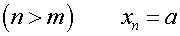
上記の式は任意のdに対して成立する。
このようにn>mのすべてのnについて、dの値がいくら小さくても、数列Xnの近似値は必ずaの近似値と等しくなる。これをビットマップ空間におけるε-δ論法と考える。この二つの空間におけるε-δ論法を用いて、ユークリッド空間とビットマップ空間の相互変換について検討する。
有名なゼノンのパラドックスのうちの三つは、ユークリッド空間とビットマップ空間の相互変換に関係しているので、ここで解説する。最初に飛ぶ矢のパラドックス(5)を解説する。飛んでいる矢はどの瞬間をとっても、その瞬間には静止している。それゆえ、あらゆる瞬間にそれは静止しているのであるから、飛んでいる矢は実は静止している。このパラドックスを神経科学の視点から検討してみる。連続についてで述べたように、視覚認知の初期段階では、静止画しか得られない。そこから運動は合成されたものであるので、神経科学的には飛ぶ矢のパラドックスは正しいことを述べている。外界に運動は実在しているかもしれないが、視覚認知の第一段階では運動は存在せず、かなり高次の段階において創作される。また映画においても、24枚の静止画を入れ替えているだけで、人間の脳の動画作成能力に頼っている。さらに網膜と同じ光電効果を利用するカメラも静止画しか撮れない。つまり網膜の光受容体が光電効果を利用しているため、真に連続的な運動は脳内にしか存在しない。ここで視覚以外の感覚はどうなのかという疑問が生じるが、視覚以外の感覚については、脳が受け取るのはすべて離散的な活動電位であるので、われわれが体で感じる感覚も実は離散的なものである。例えば自転車に乗って走っている時に風を受けている感覚は、離散的な活動電位から構成されている。連続的に風を受けているように感じるのは、脳が活動電位を情報処理した結果である。このように神経細胞の活動電位が、大脳に入るまでの段階には運動は存在せず、その意味では飛ぶ矢のパラドックスは間違いではない。
次にアキレスと亀のパラドックスを記載する。英雄アキレスと亀が競争する。アキレスは足が速いのでハンデをつけて、亀より後ろの位置から同時にスタートする。アキレスが亀を追い越すためには、まず亀の出発点に到達しなくてはならない。しかしその時には亀はもっと先の地点にいる。そしてアキレスがその地点に到達した時には、亀はさらに先の地点にいる。アキレスが亀のいた地点に到達する度に、いつでも亀は少し先に進んでいる。だからアキレスは、いつまでたっても亀に追いつけない。このパラドックスは無限ループになっており、ユークリッド空間だけで考えても解決しない。そこで現実との接点を作るために、観察者がアキレスが亀に追いついた瞬間を写真に取るという課題を加える。そうすると第一にシャッタースピードの問題が発生する。どうしてもシャッタースピードには限界があり、瞬間には時間の幅が生じてしまう。もしもそれが0であれば、写真自体が不可能になる。さらに解像度の問題があり、識別可能な最短の長さdが存在する。まず話を単純化するために、カメラのシャッタースピードは非常に速いと仮定する。観察者は競技場のスタンドから望遠レンズで写真を撮るとして、解像度をd=1cmとする。アキレスの速度を10m/sとし、亀の速度を1m/sとし、ハンデを10mとする。この条件ではスタートから1.11秒後から1.12秒後の間に写真を撮れば、アキレスが亀の差は1cm未満となり無視できるので、目的とする写真が撮れる。ここでより一般的に考察するために、アキレスが亀の前にいた地点に到達した回数をnとし、そのときのアキレスと亀の差をXnとすると、メートルを単位としてXn=1/10n-1となり、この数列は単調減少する。先程はカメラの解像度は仮にd=1cmとしたが、現実には解像度dは可変である。現時点でも高性能のカメラを用いることも可能であり、将来はより高性能なカメラが開発されると思われる。ところが、どんなに高性能なカメラでも解像度dは有限であるので、nを十分に大きくとれば必ずXn<dとなるので、常にXn=0となる。すなわちXnは0に収束するといえる。このようにアキレスと亀のでパラドックスは頭の中の世界のものなので、写真を撮るという現実の動作を加えると成立しなくなる。言い換えると、架空のユークリッド空間での推論は、必ず現実の自然数に変換されなければならない。このように人間の情報処理は、離散的な自然数を用いる情報処理と、連続的なユークリッド空間を用いた情報処理の相補性によって成立する。
人間の脳は活動電位を通じてしか外界を認識できない。外界からの情報は感覚器において、すべて活動電位に変換されてしまう。そこで外界を推測してユークリッド空間を脳内に創造したと思われる。これは本当に世界がユークリッド空間であることを意味しない。世界をユークリッド空間であるとして、時間と空間の連続性を認めると、ニュートン力学が成立する。ニュートン力学は質点の軌道を計算出来るのが利点であるが、もしも空間の連続性を本当に認めると、ゼノンの分割のパラドックス(6)によって、質点の移動は不可能になってしまう。もしも質点が少しでも移動したとすると、現在の位置と出発点の中間点を通過しなくてはいけない。その中間点まで到達するには、その前に出発点と中間点の中間の地点を通過しなくてはいけない。これは無限に繰り返される。つまり隣接する点が存在しない以上、どんなに近い点に到達するにも無限の点を通過しなくてはならない。つまり質点は移動できなくなってしまう。こう考えると、現実はユークリッド空間そのものではないはずである。
このパラドックスは、世界を連続と考えると矛盾が生じることを示したものである。このパラドックスに対する対処法を考えるため、もう一つの形の分割のパラドックスについて考察する。物体が目標地点に向かって進んでいる場合を考える。まず最初に出発点と目標地点の中間点に到達しなくてはならない。中間点に到達すると、そこを出発点として目標地点との中間点に到達しなくてはならない。その中間点に到達しても、また次の中間点に到達しなくてはならない。これを無限に繰り返すことになるので、無限の過程を経なければ物体は目標地点には到達しない。これは第二の形の分割のパラドックスであるが、出発点と目標地点の間の距離を1として、この過程をm回繰り返したとき、残った距離は1/2mとなる。ところがこれは架空の連続的なユークリッド空間での事である。そうすると現実の世界に合わせるには、最終的にはビットマップ空間に変換されなくてはならない。ここで最短の長さをdとする。そうすると1/2m<dとなるようにmをとると、残った距離は0で近似されることになる。しかもこれは任意のdに対して成立する。これは将来文明が進歩して、いくら測定精度が増しても、残った距離が0で近似されるようにmを決めることが可能であることを意味する。つまり繰り返しの回数さえ大きくとれば、ユークリッド空間からビットマップ空間への変換後には、必ず残った距離は0となる。つまり第二の形の分割のパラドックスは、ユークリッド空間のみで議論する場合は一見パラドックスであるが、ビットマップ空間への変換を前提とすればパラドックスは存在しない。ここでもう一度最初の形の分割のパラドックスを考えてみる。まず物体の運動を検出するには上記の議論どおり、最短の長さd以上は動かなければ検出できない。次に自分が運動する場合、α運動ニューロンの1個の活動電位は、1個の運動単位を動かしてしまう。すなわち運動にも最小単位が存在する。つまり運動を観察する場合も、運動を行う場合も、最初に離散的な活動電位があり、そこから連続的な運動が合成される。そのため運動の最小単位が存在するのであるが、我々の意識は世界を連続と認識しているので、それに気がつかないのである。結論として、最初の形の分割のパラドックスも成立しない。
このように連続と離散は相補的な関係にあり、両方を用いないと世界を記述できない。ただし、それは人間の神経系がそうなっているだけであり、真実の世界はどうなっているのかは不明である。感覚器が外界の情報を活動電位に変換してしまうので、脳は直接に世界に接することが出来ないのである。こう考えると、神経細胞の活動電位のパターンは、現実の影絵のように思えてくる。やはり我々は洞窟の比喩における囚人であり、世界を洞窟の壁に映った影として認識するしかない。真実はまだ謎であり、世界は連続であるのか離散的であるのか、あるいはどちらでもないのか、謎は残されたままである。
参考文献
(1) J. G. Nicholls et al.: From Neuron to Brain 4th ed., Sinauer Associates,Inc.(2001)
(2) E. Kandel et al.: Principles of Neural Science 4th ed., McGraw-Hill(2000)
(3) ユークリッド:ユークリッド原論,中村幸四郎・寺阪英孝・伊藤俊太郎・池田美恵訳,共立出版(1971)
(4) 田島一郎:イプシロン-デルタ,共立出版(1978)
(5) 野坂昭弘:逆説論理学,中公新書(1980)
(6) 林晋編:パラドックス!,日本評論社(2000)
前のページ | 目次 | 次のページ