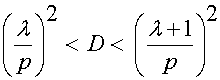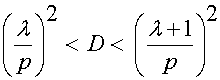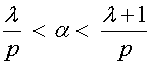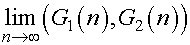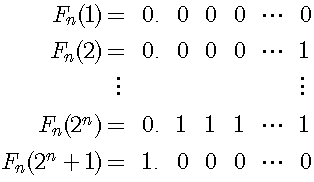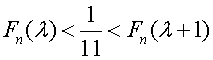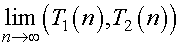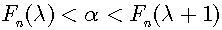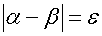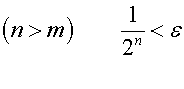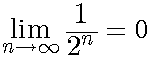実数とは何か

　これまでの議論を再確認する。人間の認識及び思考の基本は生命を「１」とする数による認識であり、神経細胞の活動電位も「１」としての性質を持つ。それに対してユークリッド幾何は空間の連続性を前提としている。そのためユークリッド幾何における線分の長さの中で、単位となる長さを1として数と長さを対応させた場合、自然数または自然数の比で表せない長さが生じる。そこでユークリッドは一般的な線分の長さを量と呼び、単位との間に比を持たない量を、無理量と呼んだ⁽¹⁾。この無理量を数として扱おうとすれば、有理数を用いて無理量を表す必要がある。これを行ったのはDedekindである。Dedekindは「連続性と無理数」⁽²⁾において、切断という概念を用いて無理数を有理数によって定義した。切断は数直線上の一点に対応しており、切断を用いて実数を定義している。ただDedekindの著作は論旨は明確であるが、あらゆる有理数の集合という表現を用いている。この表現は実無限を意味するので神経科学の立場では受け入れられない。そのため、このページでは無限ループを用いて、可能無限の立場から切断という概念を規定する。無限ループのアルゴリズムとしては、下に示す無限と連続で述べたアルゴリズムが基本となる。

S(n)=1　　　　　（=の記号は代入を意味する）
n=S(n)
上位からのモニターと命令
S(n)=n+1
ステップ2に戻る

このアルゴリズムをn回繰り返せば、自然数n+1が生じる。無限ループの意味を可能無限の立場から考えると、いくらでも繰り返し可能となる。結果として自然数に最大の数は存在しないという意味となる。すなわちいかに大きな数Nを考えても、このアルゴリズムによってN+1を作ることが可能である。このアルゴリズムは無限ループであり静止しないので、上位からのモニターが必要である。これは神経系では一般的なことであり、人間の中枢神経系は下位のループを上位の神経系がモニターし、必要に応じて制御する構造になっている。呼吸を例に取ると、通常は呼吸は全く無意識に繰り返される。ところが何らかの理由で人が興奮すると、上位の神経系の働きで呼吸が速くなる。さらに随意的に呼吸を制御したり止めたりも出来る。これが心臓の鼓動となると、より自律的となり、上位から無意識に制御されるが、意識的に止めたりは出来ない。これを上記のアルゴリズムではステップ3に、上位からのモニターと命令して示した。このアルゴリズムでのステップ3の例として、nをモニターしてn=100となれば、一から百まで漢数字で書き出すという命令等が考えられる。ここには自由に命令を付け加えることが可能である。次に可能無限の立場で、このアルゴリズムを基に有理数の切断を作るのであるが、議論を単純化するために0から1までの有理数に限定する。また上位からのモニターは、簡略化のため今後は省略する。まず分母が1の分数から始めて、順番にすべての有理数を順番に書き出す。分母が1の有理数は0と1のみであるので、この数列をA(1)と名付ける。分母が2の場合は、A(2)=(0,1/2,1)であり、分母が3の場合は、A(3)=(0,1/3,2/3,1)となる。以下のアルゴリズムは、この数列をA(1)から順番に限りなく作り出す。

S(n)=1　（=の記号は代入を意味する）
n=S(n)
数列A(n)を作成する。
S(m)=0
m=S(m)
m/nを数列A(n)のm+1番目の項として、数列の一番後ろに付け加える。
m==nであればステップ10に進む。（==の記号は等号を意味する）
S(m)=m+1
ステップ5に戻る
S(n)=n+1
ステップ2に戻る

このアルゴリズムをn回行った時点で、作られた数列A(1),A(2),A(3),…,A(n)を並べた表G(n)は、0から1までの区間において、分母n以下のすべての有理数を含む。この表を用いて、無理数を有理数の切断として定義する。ここで一例として、0＜D＜1で有理数の平方でない数Dを考えると、Dの平方根αは無理量となる。ここでαを表G(n)に含まれる任意の数列A(p)中の分数と大きさを比較する。そうすると以下の式を満たすλがただひとつだけ存在する。

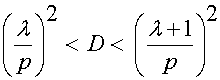
その結果、以下の式が成立する。

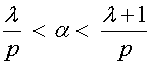
これにより数列A(p)はαより小さい数からなる数列A₁(p)と、αより大きい数からなる数列A₂(p)に分かれる。同様にA(1)はA₁(1)とA₂(1)に分かれ、以下も同様に各数列は切断され、最後にA(n)はA₁(n)とA₂(n)に分かれる。このようにして表G(n)全体が、αより小さい数の集まりG₁(n)と、αより大きい数の集まりG₂(n)に分かれる。この有理数の分類を、分母n以下の有理数の切断と呼ぶことにし、(G₁(n),G₂(n))で表す。次に(G₁(n),G₂(n))を作るアルゴリズムをいくらでも繰り返し可能として、これを極限の記号を用いて以下のように表す。

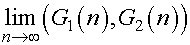
ここで0から1までの区間における任意の有理数x/yを考えると、上記のアルゴリズムをnがyより大きくなるまで繰り返せば、x/yは必ずG₁(n)またはG₂(n)に含まれる。この方法で0から1までの区間の任意の有理数を、αより大きい数と小さい数に分類することが可能である。これはDedekindの切断を可能無限で表したものと考えられる。

　ここまでの議論は分数を用いて行ったが、分数は分母が大きくなると扱いが煩雑になり、実用上は小数のほうが簡便であるので、小数で上と同様の議論を行う。話を単純にするため、小数点以下n桁の有限二進小数で無理量を近似する方法を考察する。その場合の誤差は、任意の無理量に対して、1/2ⁿ未満となる。0から1までの閉区間のn桁のすべての二進小数の表を作るアルゴリズムを簡略化して以下に示す。

S(n)=1　（=の記号は代入を意味する）
n=S(n)
表T(n)を作成する。
S(m)=0
m=S(m)
小数点以下n桁のm+1番目の二進小数をF_n(m+1)とする。
m/2ⁿをn桁の二進小数に直して、0を省略せずに二進小数F_n(m+1)として書き出す。
m==2ⁿであればステップ11に進む。　（==の記号は等号を意味する）
S(m)=m+1
ステップ5に戻る。
S(n)=n+1
ステップ2に戻る。

　このアルゴリズムをn回行った時点で作られた表T(n)は、0から1までの閉区間において、小数点以下n桁のすべての二進小数を含む。それを以下に図示した。ここでの注意点として、ここで扱う数は数直線上の点であるので、ユークリッド空間における理想的な数を表す。例えば0.00は小数点以下第二位までを有効数字とした現実の数を表すため誤差を含む。それに対してユークリッド空間の数は誤差を含まず、0と表されるべきであるが、表記上の統一性を保つため、ここでは0=0.00…0として表した。

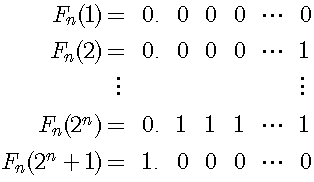
この表T(n)には二進小数で表せない有理数は含まれない。そこで例として1/3を考える。1/3は二進数であらわすと1/11となる。1/11をT(n)の各項F_n(1),F_n(2),…,F_n(2ⁿ+1)と比較する。そうすると以下の式を満たすλがただひとつだけ存在する。

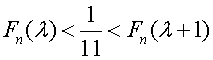
数列T(n)は1/11より小さい数からなる表T₁(n)と、1/11より大きい数からなる表T₂(n)に分かれる。このようにn桁の二進小数を大小二組に分けることを、n桁の二進小数の切断と呼ぶことにし、(T₁(n),T₂(n))で表す。ここで(T1(n),T2(n))を作るアルゴリズムをいくらでも繰り返し可能として、これを極限の記号を用いて以下のように表す。

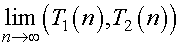
ここで0から1までの区間における任意の二進小数xがy桁であったとすると、上記のアルゴリズムをn=yとなるまで繰り返せば、xは必ずT₁(n)またはT₂(n)に含まれる。この手順をいくらでも繰り返し可能とすれば、任意の桁数の二進小数を大小二組に分けることが可能である。これは桁数に限定のない二進小数の切断なので、単に二進小数の切断と呼ぶことにする。こうすると二進小数の切断として、二進小数で表せない有理数を定義できる。次に任意の無理量αについて、無理量αと数列T(n)の各項F_n(1),F_n(2),…,F_n(2ⁿ+1)との大きさを比較する。そうすると以下の式を満たすλがただひとつだけ存在する。

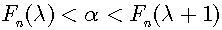
これにより数列T(n)はαより小さい数からなる数列T₁(n)と、αより大きい数からなる数列T₂(n)に分かれる。ここで0から1までの区間における任意の二進小数xがy桁であったとすると、上記のアルゴリズムをn=y回以上繰り返せば、xは必ずT₁(n)またはT₂(n)に含まれる。こうすると有理数の切断と同様に、二進小数の切断として無理数を定義できる。次に二進小数の切断が数直線上の一点に一致することを示す。数直線上の一点であるαの近くに点βが存在し、二点間の距離がεであるとする。

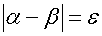
ここでαを挟む二項F_n(λ)とF_n(λ+1)の差はd_n=1/2ⁿであるので、任意の正の数であるεに対して適当な数mを選択すれば、mより大きい全てのnにおいて以下の式が成立する。

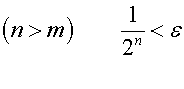
つまり点βがいくら点αに近くとも、nを大きくとればβはαを挟む二数の外側になる。すなわちαによる二進小数の切断は数直線上の一点αと一致する。結果として数列d_n=1/2ⁿは、nを限り無く増加させると0に収束する。このαによる二進小数の切断は有理数を切断しており、上に述べたようにDedekindの切断を可能無限で表したものと一致する。

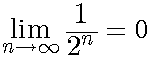
　こうして二進小数の切断は数直線上の一点に対応することになる。数直線上の一点は、二進小数または循環小数に対応する場合と、数に対応せず無理量に対応する場合がある。このうち二進小数自身による切断および循環小数による切断は有理数を表す。それ以外の切断は無理量を表すが、無理量は現実の世界における数ではない。しかし二進小数の切断は数によって定義されるものなので、ユークリッド空間限定での数として、無理数を数の仲間に加える。またDedekindの「連続性と無理数」においては、有理数による切断について、切断を引き起こした有理数自身は、大きいほうの組に入れるか小さいほうに入れるかは随意であると述べられており、Dedekindはこの二つの切断を、本質的には別のものと見なさないと述べている。こうして可能無限の立場から、ユークリッド空間限定の数として実数の定義を得たことになる。ここまでの議論は幾何学的イメージの助けを多く借りている。それに対して、Dedekindの「連続性と無理数」においては、数論は幾何学に頼らずに展開されるべきと述べられており、幾何学的イメージを排除しようとして「あらゆる有理数の集合」という表現を用いたと考えられる。これを神経科学の視点から見ると、数には生命に由来する実体があるので、数の無限集合は認められない。ところが同じ「連続性と無理数」に幾何学的記述がある。直線上の一点は直線を二つの半直線に分け、一方の半直線上の任意の点は、もう一方の半直線上の任意の点より左側にあるような分割を引き起こす。このときに直線上の点を数として解釈すれば、「あらゆる有理数の集合」という表現になる。ここで点を数として解釈せず、「数直線上にはあらゆる有理数に対応する点が、可能性として存在する。」と表現すれば、可能無限の立場になる。当時は数とは何かという定義はなされていなかったため、Dedekindは数と点を同義と考えたのではないだろうか。ただし、これは表現の問題であって、Dedekindの「連続性と無理数」をよく読むと「あらゆる有理数の集合」はそう表現されているだけで、意味としては半直線と同義に用いられている。つまりDedekindの「連続性と無理数」の内容は、そのまま可能無限として解釈可能である。そして無理数は幾何学的イメージから生じた数なので、幾何学的イメージの助けを借りて定義される。

　ここで確認すべきは、長さも幅も0である点は実在ではなく、可能性としての存在であるということである。点と線と面の関係で述べたように、あくまでも点は線の切断なのである。ところが点の数を数えたり、実際に線を切断したり、目盛りをつけたりすると、点は実在化する。図1に原点より右側のを数直線を示した。…,F(λ),…は、nは省略しているがn桁の二進小数をあらわし、αは無理量をあらわす。

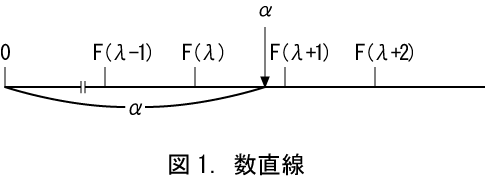
上に述べたように、ユークリッド空間における点には実体がないのに対して、「1」から構成される数は実体そのものである。そのため数で長さを近似する場合、直線上に無限個の「1」が実在すると考えてはいけない。あくまでも可能性として存在すると考えるべきで、実在の数は有限である。可能無限の特徴として、具体化した瞬間に無限でなくなるという性質がある。そのため図1においても、ある程度目盛りをつけた段階で、可能性としてはいくらでもつけられると示すに留める。これは次のような話を考えるとわかりやすい。子供同士で大きな数をいったほうが勝ちのゲームをするとする。この場合、相手に先に数を言わせて、それより一つ多い数を言えば勝ちになる。たとえば自分が漢字文化圏では最大の数である無量大数を知らなくても、相手が無量大数と言えば、こちらは無量大数一と言えば勝ちである。次に大人の場合について考えてみる。人類と同等の能力を持ち地球と同じような星に住む宇宙人がいたとする。人類と宇宙人はどちらが大きな自然数を書き出せるかで、両者の運命を賭けて勝負するとする。この勝負においてはアラビア数字の0を書き続けるような作戦は不利である。字数が多くなればインクと紙を大量に消費し、最終的には地球上の資源を消費し尽くしてしまう。そこで数の表し方が重要であるが、10の68乗をあらわす無量大数より大きいのは、20世紀に作られたgoogolであり、10の100乗をあらわす。さらに大きいのはgooogolplexであり、10のgoogol乗をあらわす。これを続けて10のgoogol乗をgooogol乗してさらにgoogol乗するというふうに数を書き出しても、やはり最終的には地球上の資源を消費し尽くしてしまう。相手はそれを見てから、それより大きな数を書き出せる方法を考えてくるに違いない。そのため、お互いに何もせずに相手が動くのを待っている状況となるであろう。これが可能無限の状況である。

参考文献
(1) ユークリッド：ユークリッド原論，中村幸四郎・寺阪英孝・伊藤俊太郎・池田美恵訳，共立出版(1971)
(2) デデキント：数について，河野伊三郎訳，岩波文庫(1961)

前のページ｜目次｜次のページ