無限と連続

　古代ギリシャでは無限について非常に多くの議論がなされたが、最終的に主流となったのはアリストテレスの考え方である⁽¹⁾。アリストテレスは可能性としての無限しか認めず、現実的な無限を認めなかった。実際に無限の大きさを持つ物体は存在しない。もしも無限に広がる空間がであったとしても、人間に観測できるのは有限の範囲のみであり、その外側については何も述べることはできない。またアリストテレスは物体を無限に分割する事は出来ないと述べ、有限の分割があるだけであり分割できる可能性があるだけであると述べている。すなわち分割に関しても可能無限しかあり得ない。また可能無限の例として、オリンピックをあげている。次のオリンピックは予定されており、その次もあるだろうし、可能性としては何回でもありえる、それを可能無限という。ところが可能性であって現実ではなく、現にギリシャの古代オリンピックは中断してしまった。同様に近代オリンピックも、将来無限に行われる可能性があるだけである。この考え方は現実の世界を考えるともっともであり、19世紀までのヨーロッパでは一般的な立場であった可能無限の立場である。実際にガウスなども無限を現実と考えてはいけないと述べている。この論文も可能無限の立場に立つものであり、これまで述べてきたように神経細胞の活動電位を1とし細胞を1として考えると、どうしても有限の範囲しか扱えない。思考実験として、人間の大脳の全ての神経細胞に番号を付け、発火している神経細胞を1として休止状態の神経細胞を0として、順番に並べて数として表すとする。これを1ミリ秒間隔で人の一生にわたって行っても、全部あわせて並べても有限の数の範囲で収まってしまう。これを人類誕生以来の全人類についてモニターしても同様である。同様に現在のコンピューターがいかに進歩しようと、有限の数しか表せない。このようにデジタルの世界は基本的には有限の世界である。ところが人間がコンピューターのプログラムを作るときに、よく陥る失敗が無限ループである。これは限りなく同じ事を繰り返すアルゴリズムであり、以下に単純な例を示す。

S(n)=1　　　　　（=の記号は代入を意味する）
n=S(n)
nを書き出す
S(n)=n+1
ステップ2に戻る

　上のアルゴリズムは、1から順番に自然数を書き出していくアルゴリズムとなる。これを何故無限ループと呼ぶのか。これがコンピュータープログラムであれば、コンピューターが止まるまで、いくらでも自然数を書き出していくプログラムとなる。そして人間はこのようなループを無限と感じる傾向がある。そのためコンピューターのプログラムでは無限ループを避けるように、色々な対策がとられている。ところが本当は、無限ループは無限に続くわけではない。このループはコンピューターが止まるまで続くが、コンピューターにも寿命があり停電がある可能性もある。もしも全人類の叡智を結集してコンピューターを動かし続けても、とても千年もつとは思えない。よしんば千年コンピューターを動かせたとしても、まだまだ無限には到達しない。このように人間が無限ループと感じる事でも、よく考えると無限ではない。例えば、夜が来れば必ず朝がくると考えるのが普通だが、太陽にも地球にも寿命があり、地球の自転は永遠に繰り返されるわけではない。仮に永遠に繰り返される現象があるとしても、有限の時間しか経過しなければ、いつまでたっても有限回である。同様に自然数を書き出すアルゴリズムでも、無限の時間を経過しなければ無限の数字を書き出すことはないのである。もっと言うと、時間そのものも永遠に続くという保証はないのである。このように考えると、ここでの無限ループは、可能無限を意味すると理解できる。次に生物学的に考察するために、上のアルゴリズムのステップ3を任意の動作に変更してみる。

S(n)=1　　　　　（=の記号は代入を意味する）
n=S(n)
任意の動作
S(n)=n+1
ステップ2に戻る

　ここで任意の動作は自由に選択できるものとすると、例えば呼吸する、腕立て伏せをする、食事をするなどの動作が考えられる。こうすると、上のアルゴリズムは動作の回数を数えるループカウンターとなる。このループカウンターに相当する神経回路を哺乳類は持っており、ラットもレバー押しの回数を数える事ができる。それを別の中枢がモニターして、ストップの信号を出すのである。これがいかに重要かを示す以下のような話がある。「ゲーデル，エッシャー，バッハ」⁽²⁾の中に、キバネアナバチの行動についての話がある。産卵期になるとキバネアナバチは穴を掘って巣を作り、コオロギを捕まえて麻酔をかけ、巣の中に入れてから産卵し、巣穴をふさぐ。卵からかえった幼虫は、巣の中で麻酔された状態のコオロギを食べて成長する。コオロギは生きているので腐らないのである。これは精巧にプログラムされた行動であり、一見キバネアナバチに高度な知性があるかに見える。ところが詳細に検討してみると、そうともいえなくなる。キバネアナバチは、コオロギに麻酔をかけ巣の前に置き、まず巣の中に入って異常がないのを確認し、コオロギを巣の中に入れてから卵を産む。その過程の途中で、コオロギを巣の前に置いて、キバネアナバチが巣の中を点検している間に、人間がコオロギの位置を少しずらしておく。そうするとキバネアナバチは、コオロギを元の位置に戻してから巣の中を再度点検する。その間に人間がまたコオロギをずらすと、またキバネアナバチは最初からやり直した。毎回同じようにコオロギをずらすと、キバネアナバチは４０回も毎回、元の位置に戻してから巣の中を点検した。そのような事はラットでも考えられず、キバネアナバチは哺乳類のようなループカウンターを、持ってはいないと思われる。この例から考えて、ループカウンターは無限ループの回避に重要であり、哺乳類の生存に役に立っている。この無限ループの話は世界各地の神話や伝説に含まれる。日本では「賽の河原の石積み」が有名である。賽の河原は三途の川のほとりにあって、幼くして死んだ子供が石を積み塔を作ろうとすると鬼が来て壊す。これを繰り返すという話である。ギリシャ神話ではシジフォスの話がある。シジフォスは岩を山の頂まで運びあげるという罰を受けた。ようやく頂上というところで、岩はその重みですぐに転がり落ちてしまう。シジフォスは永遠にこの作業を続けなければならない。このような話は人間に恐怖感を引き起こす。これは、もしかすると本能的に無限ループを避けようとする神経回路が働いているのかもしれない。そのことが今までは無限に関する議論を曖昧にさせてきた可能性がある。つまり無限ループは無限という名前が付いているが、あくまでも可能性としての無限であり、現実に無限が存在しているわけではない。ところが人間がそれに恐怖を感じるので、現実の無限と感じてしまう。

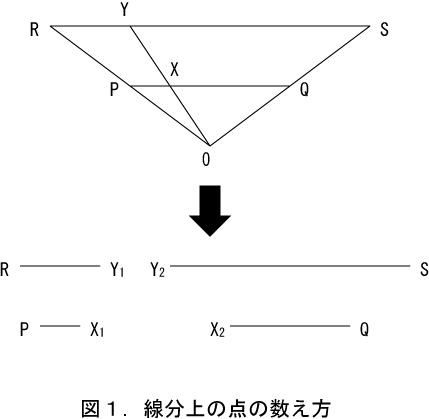
　ここまでの議論での無限とは無限ループのことであり、これはアリストテレスのいう可能無限である。この場合はコンピューターで無限を扱える。これは数すなわち自然数としての無限である。それに対して連続は感覚に属するので、これを数に変換する必要がある。連続についてで述べたように、アリストテレスによると、連続の最も大きな特徴は、いくらでも分割できることである。これを連続の定義とすると、連続を数と結びつけることが可能となる。具体的に連続的な線分上の点の数を数えてみる。まず点と線と面の関係で述べたように、点は線の切断によって生じるので、任意の長さの線分から点はいくらでも生じる。図1に任意の長さの線分PQと、PQの2倍の長さの線分RSを示し、点の数を比較してみる。図1の上図のように点OからPQを通る任意の直線をひくと、PQ上の点XとRS上の点Yは1対1に対応する。そこでより厳密に考察してみる。線分OYは幅0であるので、当然点Xも点Yも大きさ0である。それでは図に描けないので、ここでは幅のない線を実体として描き、XをPQの切断とし、YをRSの切断として図1の下図に示す。図では点XはX₁とX₂に分割され、点YはY₁とY₂に分割される。点の長さは0なので、線分を点によって切断しても全体の長さは全く変化がない。いくら切断しても長さに変化はないので、点の数は長さとは全く関係ない。むしろ切断の方法が問題であり、この方法では何回切断しても点の数は等しくなる。つまり図1の下図で、線分RX₁と線分PY₁の長さの比は2対1であるので、点Oを加えれば図1の上図と相似の図が描ける。このようにして無限ループとなり、常に線分PQ上の点と線分RS上の点に1対1の対応が成り立つので、二本の線分上の点の数は等しいことになる⁽³⁾。

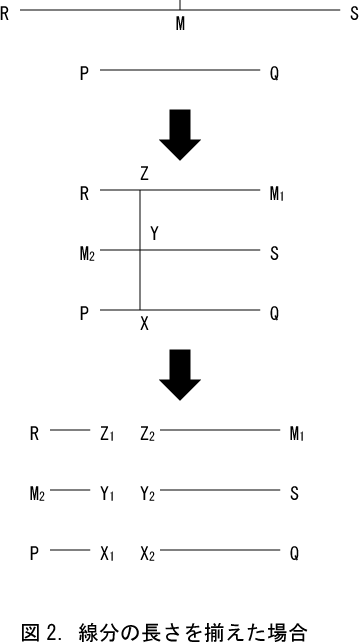
　次に図1の上図の線分RSを中点Mで2等分する。そして線分PQと線分と線分RM₁とM₂Sを並べて図2の真ん中の図に示した。ここでPQ上の任意の点XからPQに垂直な直線をひくと、PQ上の点XとM₂S上の点Y及びRM₁上の点Zは、それぞれ1対1に対応する。つまり点Xに対して、点Yと点Zの2点が対応する。次に点X,Y,Zで各線分を切断すると下図となる。ここでRZ₁:M₂Y₁:PX₁=1:1:1となるので、先程と同様に図2の真ん中の図と相似形となる。すなわちこの方法では線分RS上の点の数は、線分PQ上の点の2倍となる。このように線分PQ上の点の数と、線分RS上の点の数の比が、1対1になったり2対1になったりするのは、点が通常の意味では実在でないからである。線分上の点は大きさも幅も0であるので、可能性として存在するというべきである。何故ならば単独で紙に書く方法がないし、単独では認識することも出来ないからである。点は線が切断された場合に生じると考えるべきである。これに関してアリストテレスによると、一つの大理石を彫って彫像を作る場合、一つの大理石はあらゆる彫像になる可能性がある。それは大理石の中にあらゆる彫像が存在するのではない。彫像は可能性として存在しているのだとアリストテレスは述べている。この喩えを二次元の切り紙に当てはめてみる。一枚の紙はあらゆる形になるが、最初から形が存在しているのではなく、形は可能性として存在している。ここで線は面の切断であるので、あくまでも面の端として線は存在する。幅のない線は単独では存在しているとはいえず、認識することも不可能である。それに対して面は光子を反射するので、網膜の視細胞によって認識可能であり、一定の面積を1と規定すれば、1として実在している。つまり実在する面に依存して、線は面の境界線として存在する。同様に線の切断である点も単独で存在しているのではない。あくまでも線の端であり、面の境界線である線に依存して存在する。そのため線の切断以前には、点は可能性として存在するものと考えられる。

　線分上の点は可能性として存在するものであり、現実に存在するものではない。そのため点の数を比較するには、点を現実化するために線分を切断するアルゴリズムが必要となる。結果として特定のアルゴリズムによって生成された点の数と、別のアルゴリズムによって生成された点の数を比較することになる。例として線分PQ上の点と線分RS上の点は、図1のように線分を切断すれば常に1対1に対応し、図2のように切断すれば常に1対2に対応する。このように点を生成するアルゴリズムによって点の数は異なってくる。どちらのアルゴリズムも無限ループをなすアルゴリズムとなり、連続に由来する無限も無限ループに含まれることになる。いろいろなアルゴリズムで線分上の点を数える事が可能であるが、アルゴリズムによって結果は異なる。また無限ループによる数え方は、全ての点を数え終えたということを意味しない。無限ループで現実的な無限を達成するには、無限の時間が経過しなければならない。

　人間の脳は有限の神経細胞から構成されており、活動電位のみに注目すれば神経細胞には興奮状態か静止状態の二つの状態しかないので、神経系全体として有限の状態しか表現できない。この場合は神経系はコンピューターと類似の有限のシステムと考えられる。有限のシステムは本来は有限しか表現できないのであるが、人間は無限ループをなすアルゴリズムに無限を感じる。例えば自然数を書き出すアルゴリズムは止める指令を出さない限り、いくらでも自然数を書き続ける可能性がある。ここでの無限はあくまでも可能性としての無限である。現実の無限を達成するには、すなわち自然数を全て書き出すには、無限の時間を経過し終えなくてはいけない。これは不可能である。つまり無限ループにおける無限という言葉は、可能性としての無限を表している。そして有限のシステムで無限を扱うには、無限ループを利用するしかないと考えられる。　次に人間が無限を感じるのは連続である。空間を連続と感じ、空間は無限分割可能と感じる。この場合も可能性としての無限であるので、空間を分割するアルゴリズムを考えれば、連続に由来する無限も無限ループとして扱える。

参考文献
(1) Aristotle：Physics，Oxford University Press(1996)
(2) Ｄ．Ｒ．ホフスタッター：ゲーデル，エッシャー，バッハ，野崎昭弘・はやしはじめ・柳瀬尚紀訳，白揚社(1985)
(3) 足立恒夫：無限の果てに何があるか，光文社(2002)

前のページ｜目次｜次のページ