点と線と面の関係
連続的な平面の幾何学を最初に公理的方法で扱ったのはユークリッドである。ここで人間の視覚情報処理と、ユークリッド幾何の関係を考察する。視覚による画像処理の基本は物体のエッジの抽出であるが、物体のエッジはユークリッド幾何で定義される線に相当する。そこでユークリッド原論(1)の第1巻の定義を6番までと、第11巻の定義を2番まで記載する。
第1巻 定義
- 点とは部分を持たないものである。
- 線とは幅のない長さである。
- 線の端は点である。
- 直線とはその上にある点について一様に横たわる線である。
- 面とは長さと幅のみをもつものである。
- 面の端は線である。
第11巻 定義
- 立体とは長さと幅と高さを持つものである。
- 立体の端は面である。
次にユークリッド原論の定義を基に、立体と面と線と点の関係を考察する。立体は長さと幅と高さを持ち、立体の端は面である。そして面は長さと幅のみを持つ。そこから面は立体の切断と考えられ、立体を切断すると切断面が生じる。同様に面を切断すると線になり、線は幅のない長さである。そして線の切断として点が生じるが、点には幅も長さもないことになる。ここで人間の視覚が影響してくる。人間の視覚の感度は桿体では光子1個にも反応する(2)が、物体の認知には光子を反射する表面が無くてはならず、面積の無い線は、直接的には認識できない。あくまでも面の端として認識される。これが立体や面の認識と決定的に異なる点である。立体と面は視覚によって認識される。ところが視覚によって線を、単独で直接認識する方法は無い。さらに、ユークリッドの定義に従うと、点は線の切断であり、幅も長さもない事になる。これでは点は単独では存在できず、ただ線の端としてのみ存在することになる。結局のところ、幾何学は人間の視覚に依存するので、光を反射する面から始めるしかない。そうするとユークリッド平面はビットマップ平面からドットを消すことによって生じたと考えるべきであり、点および線から構成的に作られたとは考えられないので、これから例を挙げて説明する。ところで、これについてユークリッドはどのように考えていたのか、今となっては知るよしもないが、ユークリッド原論の定義を検討してみると、一番目に点の定義が出てくる。この定義の順番から考えて、ユークリッドは点から線を、線から平面を構成したかったのではないかと思われる。ところが原論の内容から考えて、そうは上手くいかず、色々と考えていたのではないだろうか。その考えを記録していたのだろうか。またユークリッドとは違う考えの数学者も、おそらく多数いたと思われる。そのようなことを考えると、紀元前43年のシーザーのアレキサンドリア攻撃によって、アレキサンドリアの大図書館が焼失したのが惜しまれる。
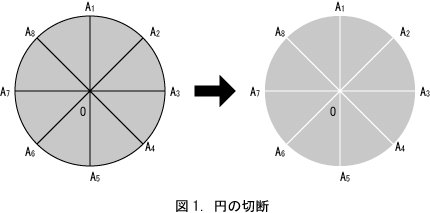
図1の左の図では、点Oを中心とした円の円周上に等間隔に点A1からA8があり、各点から中心に向かって、それぞれA1OからA8Oまで8本の線分が引かれている。ただ、この図では黒い幅のある線で線分は表現されている。ところが本来は線は幅0の切断である。そこで思考実験を行う。円形の紙を理想的な鋭利なカッターで、幅0で八等分に切断する。幅0では見えないので、断片を少し動かして、間に隙間を空ける。これが図1の右の図であるが、あくまでも幅0で切断するという点が重要であり、あくまでも架空の思考実験である。現実にこれに近いイメージを得るには、実際に円形の紙をカッターで八等分に切ってみる。より身近にはピザを八等分したイメージがこれに近い。次に、線分A1Oにおいて二つの端点を考えると、端点A1と端点Oは一対一に対応する。同様に線分線分A2Oにおいて、端点A2は端点Oに対応し、以下同じようにA8まで8個の端点に点Oは対応する。一つの点が八つの点に対応するのは、点の幅と長さが0であるあから可能となるのである。イメージとしては、円形のピザを切り分ける場合、中心点は何回もナイフが通るが、空白であるので何の抵抗もないのと同じ感じである。このように一点は任意の数の線分の端点となる。次に反対側の端点である円周上の点A1から点A8を重ね合わせても一点となり、やはり幅も長さも0となる。このように円周上の点をいくら多く集めても長さは0である。また線の面積は0であるので、円を線分によっていくら分割しても面積は変わらない。
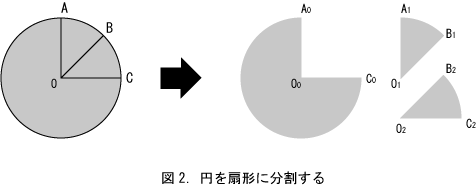
次に図2の左の図では、円周上のAとBとCの3点から、中心Oまで3本の線分がある。この線分によって円を切断し、3つに分けたのが右の図である。こうすると、線分AOは線分A0O0と線分A1O1の2本の線分に分かれる、同様に線分BOと線分COもそれぞれ2本の線分に分かれる。このように一つの線分による切断により、二つの線分が生じる。また、図のように円を3つに切り分けると、点Oは点O0と点O1と点O2の三つの点に分かれる。このように点に関しては、1個の点を任意の数に分割可能である。
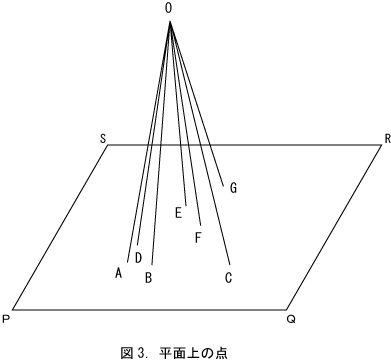
次は点と面の関係について考察する。図3において、平面PQRSと平面より高い位置に点Oが存在するとする。ここで平面上に点Aから点Gまでの七つの点から点Oまでの7本の線を引く、点Oは各線分の端点であるが、高さも幅も長さもない。そうすると、各線分のもう一方の端点である点Aから点Gまでを合わせた面積も0となる。次に平面上の任意の点から点Oまでの線を引くことが可能である。その場合も、各線分の二つの端点は一対一に対応するので、平面上のいくら多くの点を集めても面積は生じない。これは図1において、いくら多くの点を集めても線にならないのと同様である。このように点から線や面は作り出せない。
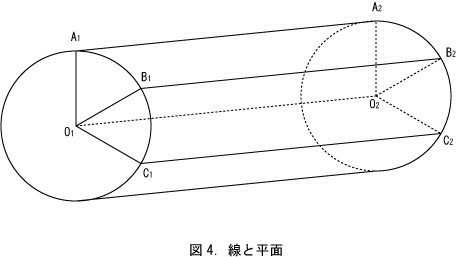
次は線と面の関係について考察する。図4に、二つの底面の中心をO1とO2とする円柱を示す。円柱の側面に直線O1とO2と平行に、直線A1A2、直線B1B2、直線C1C2の三本の直線を引く。この三本の直線と直線O1O2の関係を考察する。各直線と直線O1O2を向かい合う辺とする長方形を考える。こうすると直線O1O2は、長方形の一辺を三つ重ねたものと考えることが出来る。そう考えると、この円柱の側面の直線O1O2と平行な全ての直線は一本の直線O1O2に重ねることが可能である。こうして線を集めても面にならない事が分かる。また、先に述べたように点を集めても線にならない。逆に面の切断として線が生じ、線の切断として点が生じる。
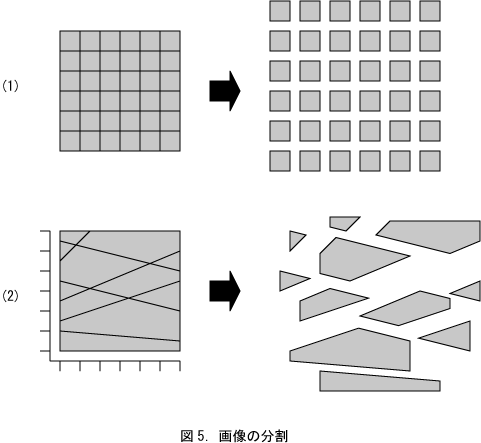
前のページでは、幅0の境界線という概念を導入した上で、画素の形を単位正方形にすることによって、ビットマップ平面からユークリッド平面を導いた。そのようにして描いたのが図5の(1)であり、単位正方形によってユークリッド平面を形成している。それをバラバラにして単位正方形に分けたのが図5の(2)である。この場合の幅0の境界線はユークリッド平面を切断するものであり、ユークリッド幾何における線に相当する。この段階では切断できる場所は、画素によって決まっている。それに対し画素を融合させて、どこでも切断可能にしたのが図5の(1)であり、実際に切断してバラバラにしたのが図5の(2)である。これは一次視覚野における画像処理に対応しており、画素は消えても、細胞の配置は網膜を再現しており、位置や距離は保存されるので、左の正方形の外側に目盛り付きの定規を描いた。ここで確認するべきは、画素に対応するのは面積であり、面積には実体があるが線と点には実体がないということである。
このように実体のない線を元にユークリッド幾何を構成した場合、大きな問題が残る。幾何学の問題を考えるのに不可欠な作図が全く出来なくなるのである。特に点は幅も大きさもないので、描くことも認識することも出来ない。これは脳内にしか連続的な平面は存在しないからである。前ページで述べたように、脳への感覚神経からの入力は、全て離散的な活動電位であり、脳から出力されるのは、離散的な運動神経の活動電位である。そのため作図をしようとすれば必然的にビットマップ画像を描くしかない。ビットマップ画像において、大きさのない点を描くことは不可能であり、最小の構成要素である画素によって近似するしかない。そうすると点は画素そのものとなり、分割不能な1となる。そうすれば点が連なったものとして線が生じ、線から面が生じる。これは無理数の発見以前のギリシャ人の考え方と一致する。私はユークリッド原論にも、その名残は認められると考える。第一巻の一番すなわち巻頭の定義は、「点とは部分を持たないものである。」とある。ところが、二番の線の定義を基に三番で点の定義を行うと、点は長さも幅もなくなり、一番の定義自体は必要ないように見える。これは一見矛盾点にも見えるが、私はユークリッドが作図の余地を残すため、わざと古い考え方を残したのではないかと考える。つまり一番の点の定義は、ビットマップにおけるドットまたは画素を意味すると考えられ、この定義により作図は可能となる。そのせいで一番と三番で点は二重に定義されたことになるが、ユークリッド自身は二つの定義の関係を、どう考えていたのだろうか。これも興味深い謎である。
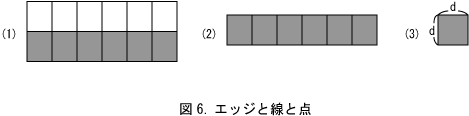
次に画素を単位正方形として描画し、エッジを表現した模式図が図6である。(1)に白と黒の境界線としてのエッジを示した。境界線としてのエッジは単独では存在できず、二つの単位正方形の境界線としてしか存在できない。そして、一次視覚野の単純型細胞は、エッジ以外に線にも反応するので、絵を描く場合は二つの単位正方形を用いてエッジを描くよりも(2)に示したように、一つの単位正方形が一方向につながったものとして線を描いた方が効率的である。そのようにして描かれた線は、(3)に示した一辺の長さがdの単位正方形から構成されている。ここでは点は画素であり、単位正方形そのものとなる。このようにすれば、幅0の線を元にしたユークリッド幾何に対して、一辺の長さがdの単位正方形を元にした作図が出来るが、それは理想の作図に対して、誤差d以下の近似となる。このようにして図を描いて幾何学を考えても大きく間違わないのは、我々がアナログ画像を見ているように思うのは、脳で作成した画像を見てそう感じるだけであり、元は網膜の視細胞の二次元ビットマップ画像だからである。ただし、現実の世界が本当は連続なのか離散的であるのかは、また別の話であり今でも謎である。ここでの議論は、ただ我々の感覚器官が外界をデジタル化して脳に送るという事と、脳から運動神経への出力もデジタルであるという事である。
参考文献
(1) ユークリッド:ユークリッド原論,中村幸四郎・寺阪英孝・伊藤俊太郎・池田美恵訳,共立出版(1971)
(2) J. G. Nicholls et al.: From Neuron to Brain 4th ed., Sinauer Associates,Inc.(2001)
前のページ | 目次 | 次のページ






