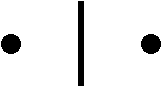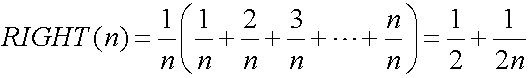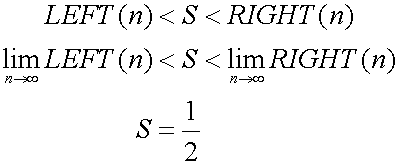- アリストテレスの輪のパラドックス
- 幾何学的原子の導入
- 直線による円の近似
- 積分とは何か
ユークリッド幾何を勉強する場合、最初に驚くのは点に大きさがないことでしょう。その上に線には幅がありません。誰もが、そんなことはあるはずがないと思うのが自然です。ところが幾何学を勉強させられるうちに、いつの間にか納得してしまうのです。私自身もユークリッド幾何を知った時には、証明の見事さに魅せられて夢中になりました。ユークリッド原論を初めて手にした時には、厳密な論理に感心し、その体系の美しさに圧倒されました。その頃になると、最初の疑問は忘れてしまいました。
次に勉強するのがデカルト座標です。これを知った時にも大きな驚きがありました。ユークリッド幾何での証明はかなり難しく、特に補助線の引き方にはかなりの技巧を要します。ところが図形を座標で表せば、補助線の必要はなくなります。デカルトの解析幾何を用いれば、式の計算で答えは出ます。図形が式で表されるとは、何と素晴らしいアイデアなのだろうかと思いました。こうなると点には大きさがないのは当然となります。そうすると、例えばy=X2という式が放物線を表すのは当たり前のように思います。しかし本当は、ユークリッド幾何と解析幾何には、おかしな点がたくさんあるのです。最も大きな問題は、ユークリッド幾何の構成で述べたように、大きさの無い点から長さのある線は構成され無いという事実です。
このようにユークリッド幾何には大きな欠点があり、デカルトの解析幾何もそれを引き継いでいます。それは純粋数学の範囲で考える限りは目立ちません。ところが数学を物理学に適用しようとすると多くの困難に突き当たります。そのような困難を解決するために微積分が開発されと思われます。微積分を開発するには、どこかで論理よりも現実を優先する考え方が必要です。
古代において、アルキメデスは数学を物理学に適用しようと試みましたが、アルキメデス自身の死によってその試みは中断します。さらにローマ帝国の崩壊の後、アルキメデスの業績は長く忘れられていました。それを受け継いだのがガリレオ・ガリレイです。ガリレオも同様に、数学を物理学に適用しようとしました。そのためには、数論と幾何学の統合が必要です。アルキメデスの著作の多くは失われていますが、ガリレオの考えの内容については今でも知ることが出来ます。特に新科学対話に出てくるアリストレスの輪のパラドックスのパラドックに関する考察は非常に面白く意味も深いので、そこを出発点として数論とユークリッド幾何の結合を試みます。
図1にアリストテレスの輪のパラドックスを示します。中心が同じで、お互いに固く結合した大きい円と小さい円があります。大きい円が一回転すると、同じように小さい円も一回転します。このときに大きい円の円周上の一点Bの移動距離を考えます。点Bは大円の円周を一回転して点Fに到達しますから、直線BFは大円の円周に等しくなります。同時に点Cは点Eまで移動しますから、小さい円の円周は線分CEと等しくなります。明らかにBF=CEなので、小さい円の円周は大きい円の円周と等しくなります。この議論は任意の大きさの同心円に適用出来ますから、全ての円の円周は等しいとなります。これがアリストテレスの輪のパラドックスです。

図1.アリストテレスの輪のパラドックス
ガリレオは、このパラドックスに解決策を与えています。円を正多角形に変えてみます。どんな正角形でも良いのですが、図2に正方形の場合を示します。正方形ABCDと一辺の長さが半分の正方形EFGHがあり、二つの正方形の中心が同じで、両者は固く結合しているとします。最初に点Bを中心に大きい正方形を回転させると、辺BCが底辺になります。順番に点B,C,D,Aを中心に回転させると、最終的に一回転して底辺ABに戻ります。この間に底辺と平行な直線上には、小さい正方形の辺は半分しか接しておらず、4カ所の空白を含みます。
この議論は多角形の辺の数をいくら増やしても成立するので、正100,000角形でも成立します。従って小さい正方形を回転させると、100,000個の空白が生じると、ガリレオは述べています。正方形を正100,000角形に代えて同じようにすれば、半分の大きさの正100,000角形は半分しか直線に接していないのです。人間の眼では正100,000角形は円と区別できないので、この場合は円を正多角形で近似した方が、現実に近いモデルが得られるということになります。よく考えると、現実に円と直線が大きさの無い点で接しているということは有り得ません。むしろ正多角形の一辺が直線に接していると見なす方が現実に近いと思われます。
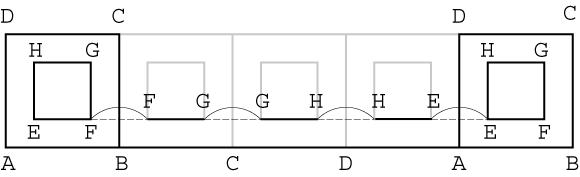
図2.ガリレオによる解決策
これで見事に解決されたように思いますが、現実に近いモデルである正100,000角形を、完全に理想化されたユークリッド平面上で円に戻してみると、とても空白があるようには思えません。図3を見て下さい。大きい円周上の任意の点Pから中心点Aまで線分を引き、小さい円と線分の交点をQとします。点BからPまでの円周の長さに線分BPの長さは等しいとすれば、円周上の任意の点Pは線分BF上の1点Pに対応します。すなわち、大きい円の半径PQAは線分BFと直交する線分PQAに対応します。
半径PQAと線分PQAは対応します。すなわち、PとQとAは1対1対1に対応します。つまり、大きい円の円周上の点の数と、小さい円の円周上の点の数、中心点Aを分割して生じた点の数は全て等しいのです。点Aは元々1点ですから、線分AD上の点は全て集めても0です。同様に線分BFおよび線分CE上の点を全て集めても長さは0です。このように考えると、ユークリッド幾何の構成で述べたように、点から長さは構成出来ないということが分かります。幅のない長さは線ですので、点から線は構成出来無いとなります
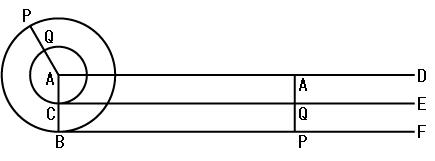
図3.点と長さの関係
やや煩雑になりますが、その理由を考察します。点から線を構成しようとすれば、必ず隣接する点が必要となりますが、隣接する点は存在し得ません。もしも隣接する2点間の距離が0であれば、2点は1点になってしまいます。もしも隣接する2点間に距離があれば、そこには線があることになり、線は無限分割可能なので、隣接する2点間には無限の点があることになります。つまり隣接する2点は有り得ません。2点の間には必ず長さ、すなわち線が存在します。そうすると点は線の端になります。
ここで点を認識することを考えます。単独の孤立点は幅も長さも0なので、検出する方法がありません。大きさ0の孤立した点は存在していないと考えるべきでしょう。それに比べると、線の端としての点は検出可能ですので、存在していると見なすことが出来ます。こう考えると、大きさ0の点は最初から存在すると考えてはいけないとなります。むしろ線を切断すると線の端として生じると考えるべきです。線分の1回の分割で、2個の点が生じます。さらに複数の線分の端点となっている点は複数の点に分割可能です。例えば円の中心点は、任意の本数の半径の端点となりますので、任意の個数の点に分割可能です。元々は1点であっても、線の切断によって複数の線の端点になります。同様に任意の長さの線分は、任意の回数分割可能です。すなわち任意の長さの線分からは任意の個数の点が生じます。つまり点は可能性として存在しているとした方が合理的です。
そうなるとやはり、ユークリッド幾何を数論と結びつけるには、どうしても画素の存在を前提として理論を構築する必要があります。ユークリッド幾何の構成で述べたように、ユークリッド平面はビットマップ画像から画素を隠して得られたものですから、画素を前提とする必然性があります。
元々ギリシャ人は、図形は自然数1に対応する画素から構成されると考えていました。ここで画素の形を考えてみます。図4の黒い点はデジタルカメラの二つの光の検出器を表します。この二つの黒い点が画素の中心となりますが、両者から等距離にある地点は中央の黒い直線となるので、必然的に画素と画素の境界線は直線となります。これは人間の網膜の視細胞もに適用することが可能です。視細胞の中心点を黒い点とすると、等しい距離にある地点は直線となります。
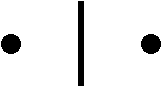
図4.画素と画素の境界線
画素と画素の境界線が直線で、画素が一様に分布しているとすると、画素の形は正多角形となります。平面を埋め尽くすことが出来る正多角形は正三角形、正方形、正六角形の三種類しかありません。他の正多角形を用いてもビットマップ画像は構成出来ますが、単位正方形はコンピューターで広く用いられていて、数学の全ての分野でも一般的です。単位正方形は自然数1に対応するので、単位正方形と他の図形の関係から、数論とユークリッド幾何の対応を考えます。
まず単位正方形を集めて長方形を作ります。ビットマップ画像の限界で述べたように、単位正方形で構成された長方形の面積は、長さかける幅となります。こうして単位正方形で構成された長方形と数の対応は明確になります。次に辺の長さが有理数の長方形に関しては、有理数は自然数の比と考えることができます。この場合も長さかける幅で面積が求められるとして問題有りません。さらに長方形を対角線で二等分すると直角三角形になります。後に述べるようにあらゆる直線図形は直角三角形に分割出来るので、直角三角形は数論とユークリッド幾何を結合する役割を果たします。
数論と幾何学を結びつけるのに大きな障害となるのが無理数です。無理数の存在を説明するために、古代ギリシャ人は多くの理論を考えました。その中で有力な理論の一つとして、デモクリトスの原子論があります。原子論によれば無理数は存在可能であり、しかも画素に近い分割不能な原子が存在します。さらに積分の創始者アルキメデスによると、デモクリトスは原子論を幾何学に適用して、円錐の体積が円柱の1/3であるという結果を得ていたとあります。
デモクリトスの著作は断片のみが残っていて、多くは失われていますがアリストテレスの著作から知ることが出来ます。原子論では世界は空虚と分割不能で変化しない原子からなり、原子には色々な形や色々な大きさの物があり、無限の種類があるとなります。原子は常に運動していて、結合したり分離したりしています。原子の形には直線も曲線もあるとなりますが、これは空虚の存在を認めているからです。これはかなり現実に合致していて、現代の視点でも良くできた理論です。
しかし、このままでは幾何学には適用できません。幾何学の世界には空虚が存在しないからです。幾何学に適用するためには、原子は無限の種類のある画素となります。幾何学の世界では画素は静止していて、図形は画素で埋め尽くされていなくてはなりません。そうすると、画素と画素の境界線は直線になります。原子論における画素は、一般的な同じ形で同じ大きさの画素とは異なるので、通常の画素と区別するために、原子論における画素を幾何学的原子と呼ぶことにします。
第一に幾何学的原子は、数論との結合を考えると、直線から構成されなくてはいけません。その上で、あらゆる直線図形を構成出来なくてはなりません。この条件に合致する図形は三角形です。図5-(1)を見てください、あらゆる直線から構成される図形は三角形に分割出来ます。次に図5-(2)に示したように、三角形は直角三角形に分割出来ます。直角三角形の面積は非常に簡単に計算できるという利点があるので、直角三角形を図形の原子と考えます。そして無限の種類の直角三角形が幾何学的原子として存在するとします。このような幾何学的原子は、解析学との相性がよいのです。合同な直角三角形を二つ合わせると長方形になります。長方形は積分の基本的図形となりますし、直角三角形は微分の基本的図形です
例えば図5-(3)に示したように、二等辺直角三角形ABCは、多数の小さな二等辺直角三角形に分割出来ます。この例では、AB:BC:CA=√2:1:1となります。このように原子論を幾何学に適用すれば、無理数は存在可能になります。何よりも、ユークリッドのように大きさの無い点を基本概念としたのでは、図形どころか平面自体が構成出来ません。その点、幾何学的原子からは直線図形と平面自体は簡単に構成出来ます。しかも長さと幅をかけて面積になる必然性があります。
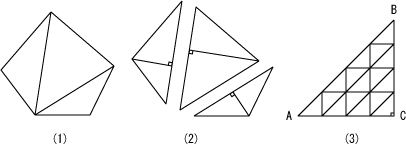
図5.図形の原子としての直角三角形
あらゆる形の直角三角形を幾何学的原子と考えますが、面積0の直線は幾何学的原子に含みません。このようにして直角三角形を幾何学的原子として、あらゆる直線図形を構成することが可能です。直角三角形の面積は簡単に計算出来るので、どんな直線図形の面積でも計算できます。これが画素から自然に連続的なユークリッド空間を導く方法です。
人間にとって曲線を認識するのは意外に困難です。ギリシャ人も長い間、円と直線しか知りませんでしたが、これは必然です。ヒューベルとウィーセルが明らかにしたように、脳の一次視覚野の単純型細胞で認識されるのは直線だけなのです。だから人間の脳で、画素を消して構成される図形は、最初は直線から構成されているのです。そして曲線はより高次の視覚野で構成されます。人間の作った多くの物が、直線から構成されているのは当然なのです。例えば箱、部屋、机、本、ノート、テレビ等々です。
次の問題は、ユークリッド幾何の構成で述べたように、点から線は構成出来ないので、ユークリッド平面で曲線を構成するのは不可能であるということです。曲線を定義するには、現代では一個の点の位置を方程式で決めて、曲線は点の集合として定義するのが自然です。例えば円であれば中心から等しい距離にある点の集合となります。例えば原点中心の半径1の円を式で表せばx2+y2=1となります。このような方法では長さが構成できないので、曲線は構成できません。無理に曲線を点の集合として定義すれば、アリストテレスのパラドックスで示したように、あらゆる円周の長さは等しくなります。つまり曲線の長さという概念が成立しなくなるのです。このような困難を切り抜けるため、ユークリッドは原論(Elements)で以下のように円を定義しました。
第7巻 定義
15. 円とは一つの線にかこまれた平面図形で、その図形の内部にある1点からそれへひかれたすべての線分が互いに等しいものである。
最初に線という言葉を出し、その線の性質として円を定義する。これは非常に巧妙な方法です。このやり方はユークリッドの常套手段で、面から線を定義し、線から点を定義したのと同じやり方です。最初に曲線が存在するものとして、そこから曲線上の点の性質を決めていくという手順になります。一見すると上手く切り抜けたように見えますが、これでは曲線の長さは定義できません。
それどころか、ユークリッドは自己矛盾に陥っています。原論の定義では幅の無い長さは線ですが、そうすると線には直線しか存在しなくなります。線という概念と長さという概念は切り離せなません。曲線の長さという概念が成立しないので、曲線自体が存在し得ないのです。これではユークリッド幾何の構成に無理があると考えるしかありません。
むしろ幾何学的原子を用いて幾何学を構成する方が自然なのです。唯一の欠点は曲線が存在できない点ですが、それはユークリッド幾何でも同様です。幾何学的原子を用いれば、微分積分によって曲線をいくらでも近似できます。曲線はいくらでも近似できる存在ですし、曲線の方程式を求めることも可能です。私はこの部分は人間の視覚情報処理の欠点であると考えていて、別の機会により詳細に議論したいと考えています。
積分の創始者はアルキメデスですが、アルキメデスは円周率の近似値を求めています。その方法を図6に示します。円周を内接する正多角形と外接する正多角形で挟みます。こうすると円周の長さは、内接する正多角形の周囲の長さより長く、外接する正多角形の周囲の長さより短くなります。こうして正多角形の辺の数を増やしていけば、円周の長さはいくらでも精確に近似出来ます。この図では正六角形と正十二角形を示しました。アルキメデスは辺の数を倍々と増やしていき、正九十六角形にまで到達しました。
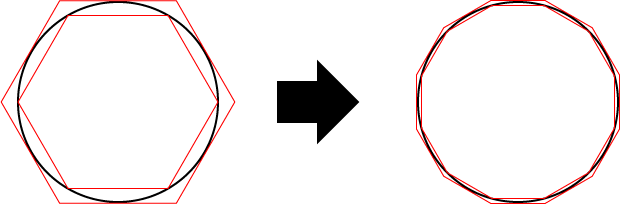
図6.多角形による円の近似
こうして円周の長さはいくらでも近似出来るのですが、ここで根本的な問題があります。円周の長さとは何かということです。直線は、幅のない長さとして定義されます。2点間の距離は、2点間の直線の長さです。円は直線を含まない図形なので、簡単には円周の長さを定義出来ないのです。アルキメデスの仕事は当時から、存在するとは限らない物を存在するものとして近似していると批判されていました。この問題に関しては別の機会に考えてみます。
曲線が存在するかどうか、その問題は一時棚上げとします。その上でユークリッド空間の点と実数を対応させたのが解析学です。そして曲線は存在するものとして、曲線の方程式を求めます。ところが曲線図形の面積や曲線の長さを求めるには、やはり幾何学的原子が必要です。面積を求めるためには長方形が基本図形となり、曲線の長さを求めるためには直角三角形が基本図形となります。積分には幾何学的原子が必要です。図7は積分の説明でよく使われる図なので、似たような図を誰もが見たことがあると思います。
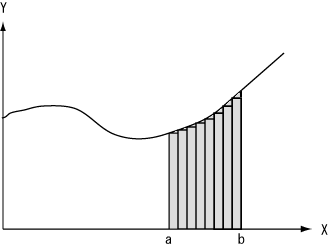
図7.積分の考え方
図7には曲線のグラフを示します。区間[a,b]について、曲線とX軸に挟まれた灰色の部分の面積を求めます。普通は曲線に囲まれた図形の面積は単純には計算出来ないので、小さな長方形に分けます。そのために区間[a,b]をn等分します。そうすると長方形の幅は(b-a)/nとなります。長方形の高さはX軸から曲線までの長さとなります。曲線の式をy=f(x)とすれば、点aでの高さはf(a)となります。こうして細い1個の長方形の面積を求め、全ての長方形の面積を合計します。ここで幾何学的原子に無限の種類があることが役に立ちます。nをいくらでも増加させることが出来るので、細い長方形の総面積は求める面積にいくらでも近づきます。これが積分の考え方です。より詳しく説明するために図8に積分の原理を示します。
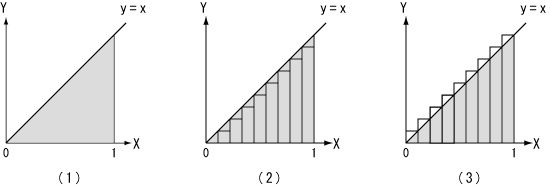
図8.積分の原理
ここでは計算を単純化するために直線に囲まれた面積を積分を用いて求めますが、原理は曲線の場合と全く同じです。図8-(1)にはy=xのグラフを示します。区間[0,1]においてX軸とグラフに挟まれた灰色の部分の面積を、積分を用いて求めます。まず区間[0,1]をn等分すると、細い長方形の幅は1/nとなります。
最初はn等分した区間の左側の点における関数の値を細い長方形の高さとします。関数y=xは単調増加するので、この長方形の面積の合計は求める面積より小さくなります。図8-(2)に区間の左側を高さとする長方形による近似を示し、これをLEFT(n)と表します。

次に同様にして、区間[0,1]をn等分して、n等分した区間の右側の点における関数の値を細い長方形の高さとします。関数y=xは単調増加するので、この長方形の面積の合計は求める面積より大きくなります。図8-(3)に区間の右側を高さとする長方形による近似を示し、これをRIGHT(n)と表します。
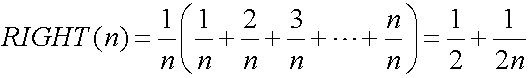
求める面積をSとすると、SはLEFT(n)より大きく、RIGHT(n)より小さくなります。nを増加させるとLEFT(n)もRIGHT(n)もSにいくらでも近づきます。Sは間に挟まれているので、Sの値はいくらでも精確に近似出来ます。ここでnをどんどん増加させていくと、Sは1/2にいくらでも近づきます。
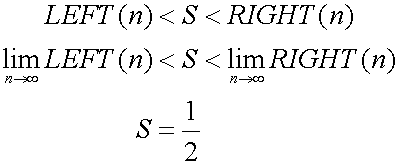
この場合は二重期謬法が使えます。まずSが1/2ではないと仮定します。例えば差が|S-1/2|=dであったとします。d>1/2nとなるようにnをとれば、Sが1/2より大きくても小さくても矛盾を導けます。必然的にS=1/2でなくてはいけません。これは二重帰謬法と言います。この方法の弱点は、確かにが存在していることを証明できないことです。この例の場合は単純化するために直線ですから、正しい値は1/2で間違いありませんし、二重帰謬法も問題ありません。それでもこの方法では、直接Sを求めることは出来ません。
同様に、この方法を一般の曲線に適用した場合、曲線で囲まれた面積を近似することは出来ますし、nを増加させることによって近似の精度はいくらでも上げることが出来ます。ところが二重帰謬法を用いても、曲線の存在自体を証明することは出来ません。幾何学的原子は長方形または直角三角形ですから、図形が幾何学的原子で構成されているなら、真の曲線は存在しないことになります。
それでも幾何学的原子を導入すると、ユークリッド幾何の欠点を補うことが出来ます。点から図形も平面も構成出来ないのがユークリッド幾何の最大の欠点ですが、幾何学的原子から平面は容易に構成出来ます。幾何学的原子を導入する最大の利点は、曲線の長さ、曲線図形の面積を計算出来ることです。しかも通常の画素からなる幾何学との相性も良いので、現実への適用も容易です。