PyQtでお手軽GUI開発♪―――は可能だったか? 第15回 無量大数の彼方に!編
さて、ついにリモートマンデルブロ並列システムの作成に入ることにします。
ワーカーリストの作成
まずはワーカーリスト(=外部からのconnectionのリスト)を作るスレッドです。
やることは下記のように超シンプルなので、チャットクライアントのときのように、スレッドの機能は単なる関数として書いて、Threadのコンストラクタで呼び出す方式にします。
def getcalcprocess(self): """外部からのコネクションリストを作成する""" address = ('192.168.10.8', 6000) with Listener(address, authkey=b'secret password') as listener: print('start mandel server') while True: #acceptが来たときしかループは回らない conn = listener.accept() print('connection from', listener.last_accepted, conn.fileno()) self.workers.append(conn)
そしてMyFormの__init__の中で以下のように初期化します。
self.living = True
self.workers = []
self.mandelserver = Thread(
target=getcalcprocess, args=(self,), daemon=True)
self.mandelserver.start()
- スレッドが動き出すと止める仕組みが面倒なので、デーモンにしています。
マンデルブロサーバー
マンデルブロ集合の計算を行うサーバーは以下のような物です。
ただしサーバーではもう計算そのものはまったく行わず、パラメータをリスト化してワーカーに送り、結果を集計しているだけです。
以下の例では各ワーカーに対して10行分のデータを計算して返してもらうようにしています。
送りあうデータは(':コマンド', データ)という形式のタプルで定義しています。
def mandel_i_rp(self, aF, bF , pwF, zoom, iw, ih, cmax, calc, app): """16Lリストの自前固定小数点化(リモート並列処理) self: MyForm aF,bF: 計算開始位置の座標(fdecタプル) pwF : ピクセルのサイズ(fdecタプル) zoom: 拡大率(この描画における小数点桁数の基礎となる) iw,ih: 計算する領域の幅と高さ(pixel) cmax: ループの最大回数 calc: 計算関数(a0, b0. cmax, dig, C4) app: QApplication """ if len(self.workers) == 0: print('計算プロセスがいません') return dig = zoom + 12 C4 = fdec.setint(4, dig)[0] #プログレスバー処理 t = time.perf_counter() self.ui.progressBar.setMaximum(ih) self.ui.progressBar.setValue(0) self.ui.progressBar.show() self.esc = False self.ui.statusbar.showMessage('Escで中断するよっ!') self.ui.statusbar.update() app.processEvents() #基本的なパラメータを指定桁数で整数化 a = fdec.setdigit(aF, dig)[0] b = fdec.setdigit(bF, dig)[0] pw = fdec.setdigit(pwF, dig)[0] #ls行ずつまとめた計算パラメータを作る ls = 10 #まとめて処理する行数 params = [] p = [] for j in range(ih): b0 = b + pw*(ih-j) p.append((a, b, b0, pw, iw, ih, cmax, dig, C4, j)) if len(p) >= ls: params.append(p) p = [] if p != []: #端数が出ていた場合 params.append(p) #ワーカーに初期化命令を送る for rp in self.workers: rp.send((':init', )) #送った分が戻ってくるまで回してないといけない rest = len(params) while True: for rp in wait(self.workers): #結果はリストなのでforでも回す msg = rp.recv() print('from {} - command: {}'.format(rp.fileno(), msg[0])) #計算結果が来た場合 if msg[0] == ':data': for l in msg[1]: self.mandeldata[l[0]] = l[1] #結果には行番号も含まれている rest -= 1 #パラメータ要求が来た場合 elif msg[0] == ':request': if params: rp.send((':param', params.pop(0))) #プログレスバー処理 if time.perf_counter() - t > 0.25: self.ui.progressBar.setValue(ih - rest*ls) app.processEvents() if self.esc == True: #ESC処理では self.resetClient() #ゴミが残るのでいったん切ってつなぎ直す rest = 0 t = time.perf_counter() #結果を全部受け取ったら終了 if rest == 0: self.ui.progressBar.hide() return def resetClient(self): """リモートクライアントをリセットする ※ディスコネクトしたら5秒後くらいにつなぎ直してくる """ for rp in self.workers: rp.send((':disconnect', )) time.sleep(0.5) self.workers.clear()
今までのものに継ぎ足し継ぎ足しで作ってるんで結構長い関数になっちゃってますが、まあ各ブロックの機能は難しくないと思います。
マンデルブロクライアント
マンデルブロ集合の計算に関しては、全てクライアントが行います。
クライアントはサーバーからパラメータリストを取得し、結果を計算して送り返します。
パラメータリストは例えば10行単位とかでやってきますが、今回の場合マシンが異なるので各プロセスの計算時間はまちまちで戻ってくる順序も不同です。そのため結果には行番号も含まれています。
- imapメソッドの場合は返ってくる順番が保証されていたので、行番号は不要でした。
# -*- coding: utf-8 -*- """ Created on Mon Mar 20 10:37:12 2017 マンデルブロ計算リモートクライアントプロセス @author: Lum """ import sys import time from multiprocessing import Pool from multiprocessing.connection import Client def multifunc(args): """1行単位で結果を計算 1行の結果を納めたリストを返す """ a, b, b0, pw, iw, ih, cmax, dig, C4, j = args r = [0]*iw for i in range(iw): a0 = a + pw*i x0, y0 = a0, b0 xx0 = (a0*a0) >> dig yy0 = (b0*b0) >> dig for n in range(cmax): x1 = xx0 - yy0 + a0 y1 = (((x0+x0)*y0) >> dig) + b0 xx0 = (x1*x1) >> dig yy0 = (y1*y1) >> dig if xx0 + yy0 > C4: break x0 , y0 = x1, y1 r[i] = n return j, r #行番号と結果のタプルを返す(どのプロセスが早く終わるか分からないので) def culc(params, p, conn): """マンデルブロ計算を行う""" t = time.perf_counter() res = [] for r in p.imap(multifunc,params): res.append(r) if time.perf_counter() - t > 0.5: conn.send((':bleath',)) #長時間止まるので時々サーバーに息継ぎを送る t = time.perf_counter() return res def main(): """サーバーに接続する""" endcode = False address = ('192.168.10.8', 6000) with Client(address, authkey=b'secret password') as conn: print('接続開始') processcount = 3 with Pool(processcount) as p: #poolを作ったり消したりしてると遅いので最初に作る while True: if conn.poll(0.001): msg = conn.recv() if msg[0] == ':param': r = culc(msg[1], p, conn) #来たパラメータを振り分けて計算 conn.send((':data', r)) #データを送り返す conn.send((':request', )) #続きのリクエスト elif msg[0] == ':init': #初期化の場合 conn.send((':request', )) elif msg[0] == ':disconnect': #終了の場合 break elif msg[0] == ':terminate': #クライアントのリモート終了の場合 endcode = True break conn.close() print('disconnect') return endcode if __name__ == '__main__': while True: try: if main(): break except ConnectionError: pass except: raise time.sleep(5) #接続が切れたら5秒待ってつなぎ直しにいく print('mandelclient 終了') sys.exit()
前回のマルチプロセス版をベースに作成しているので2段階構成で複雑になっていますが、シングルプロセスにして必要な数をOS上で立ち上げるというのもありだったかもしれません。そうしたらもっとシンプルな構成になったでしょう。
あと、エラー処理とかも適当ですが、気にしないようにしましょうw
努力は報われたか?
それは何はともあれ速度を測ってみることにします。
まずはいつも通りのパラメータでループ回数2000回でやってみます。
使ったサブマシンはIntel Core i5-2410M 2.30GHzの搭載されたノートパソコンで、このCPUも2コア4スレッドです。
すると……
#ループ2000回
関数 実行時間 速度比 補足
-------------------------------------------------------------------
i_mandel1 34,239 ms 1.00 シングルプロセス(メイン)
i_mandel2 19,391 ms 1.77 マルチプロセス(メイン)
i_mandel2 21,080 ms 1.62 マルチプロセス(サブ)
i_mandel3 19,623 ms 1.74 リモートプロセス(メインのみ)
i_mandel3 20,869 ms 1.64 リモートプロセス(サブのみ)
i_mandel3 10,756 ms 3.18 リモートプロセス(メイン+サブ)
-------------------------------------------------------------------
サブマシンはCore i5ですが少し古いので、メインマシン(Intel Core i3-4000M 2.40GHz)とほぼ互角といっていいでしょう。
マルチプロセスとリモートプロセスではほぼ時間の差はありません。サブマシンの方はむしろリモートプロセスの方がやや速くなっています。これはリモートクライアントの場合Poolオブジェクトを最初に一回作ってそれをずっと使っているので、それで転送時間のロスなどが相殺されているのかもしれません。
そしてそんな2台を並列したら、シングルプロセスのときの3.2倍弱となっています。
何だか思ったほどでもないような気がしますが―――しかし計算時間が短いといろんなオーバーヘッドが効いてきそうなので、ループ回数を増やしてやってみます。
#ループ4000回
関数 実行時間 速度比 補足
-------------------------------------------------------------------
i_mandel1 67,888 ms 1.00 シングルプロセス(メイン)
i_mandel2 37,823 ms 1.79 マルチプロセス(メイン)
i_mandel3 20,956 ms 3.24 リモートプロセス(メイン+サブ)
-------------------------------------------------------------------
さっきより速度比が上がってきました。ではもう少し回数を増やしてみると……
#ループ8000回
関数 実行時間 速度比 補足
-------------------------------------------------------------------
i_mandel1 135,349 ms 1.00 シングルプロセス(メイン)
i_mandel2 74,246 ms 1.82 マルチプロセス(メイン)
i_mandel3 38,542 ms 3.51 リモートプロセス(メイン+サブ)
-------------------------------------------------------------------
時間が長ければ速度比もUPしています!
マルチプロセスのときの速度比が1.8倍くらいなので、1.8×2 = 3.6倍がリモート並列処理で出せる限界と考えれば、まあまあな結果と言えるでしょうか。
それでは続いてもう一台追加して3台でやってみましょう。
今度のマシンは一応デスクトップですが、搭載されているのはAMD E2-1800 APU 1.70GHzというショボい奴で、動画視聴専用に買った物だったんですが、まずループ2000回でやってみると……
描画時間: 9316.7 ms
何だかほとんど変わってませんが……
ループ4000回だと?
描画時間: 23480.7 ms
えっと―――2台のときの20,956 msより遅くなってます!
ls値(1回にまとめて計算する行数)を調整したら一度は17827.3 msなんて値も出ましたが、基本的にばらついて一定しません。
そこで追加したマシン単体で速度を測ってみると、ループ500回で……
描画時間: 18831.2 ms
メインマシンでは5,732 msぐらいですから、3倍以上遅いです。
要するに速度が揃っていないマシンで並列処理する場合は、個々の速度に合わせて送るデータ量を変えるようにしないとダメなのだということのようです。
しかし、今のルーチンでは一律の分割にしか対応していないので、プロセスごとに行分割数を変えられるように修正しなければなりませんが―――そもそも3倍も遅ければ頑張ってそんな調整をしてもよくて30%くらいしか速度上昇は期待できないわけで、さすがにそろそろ疲れてきたのでやめることにします。
無量大数の彼方
というわけでとりあえずこのくらいが我が家できる限界のようです。
結局シングルプロセスの場合に比べて3.5倍程度だったということですが―――Numbaのときに170倍なんて数字を見たあとなので大したことのない結果のように見えますが、1時間かかっていた描画が20分以下になるわけですから、一般的には相当の成果というべきでしょう。
それにちょっとした小技を駆使すれば、これでもマンデル世界周遊は十分堪能できます。
というのは、表示していた画像の1辺の長さを1/4にすれば面積は1/16、すなわち16倍の速度で描画できます。更にそれが3.5倍ということは、そんなサムネイル画像なら56倍の速度で描けるということです!
- またさきほどの画像(ループ8000回)をCython関数で表示してみれば 1,128 ms 程度かかったのですが、今の結果はそれよりたった34倍しか遅くないとも言えますし♡
また周遊していて「あ、これは取っておきたいな!」という場所はそうそうはないわけで、ならば普段はサムネイルで見ていて、ここぞというときだけ拡大表示をすればいいわけです。
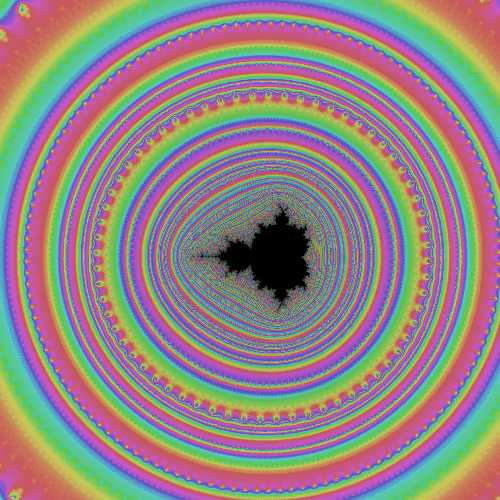
―――というわけで以下の画像はそんな風にして見つけた、我が家の最小マンデル画像です。
画像のパラメータは以下のようになります。
a=-121196956243322476017002630862464943201162004021012714960012871046886647962260363002×2-275
b=-5977620834308090852731453170213033535974435018005854755714623171861131107732042×2-275
pw=2-275
cmax=100000
10進小数で表してみれば……
a=-1.99637859817836551138524329341609141317919645181161071798016214240476678608697459760874
b=-0.00009846447197633543694465711869726262041015803722893731276473986449846432076683881463
pw=0.00000000000000000000000000000000000000000000000000000000000000000000000000000000001647
ちなみに前述の通り、数字の桁数が増えればその2乗に比例して計算時間がかかるようになるので、精細になればなるほどどんどん時間がかかるようになります。また細かければ細かいほどループ回数を増やす必要も出てきます。
そんなわけで上の画像の場合、125*125のサムネイルでも2分以上かかってしまい、実際に描画するのには1時間近くが必要になります。
下は低倍率で見たマンデルブロ集合の全景ですが、上のちびマンデルと見た目の大きさは大体同じです。下の1ピクセルサイズが2-6なので、上記の画像は左に伸びた尖った角の先端部付近を2269倍拡大しないと見えてこないことになりますが……
これがどんな数かというとPythonなら簡単に計算できて、普通に書き表せば……
2269 = 948568795032094272909893509191171341133987714380927500611236528192824358010355712
―――指数表記で表せば約 9.485687950320943×1080となりますが、ウィキペディアによれば観測可能な宇宙の大きさは直径930億光年 = 8.798×1026m なんだそうで―――これでは全然足りません。
物理的な意味を持ちうる最小の距離をプランク長といって、その長さが1.616×10-35m なのでこれを単位に表せば、宇宙の大きさは約5.444×1061(= 約54那由他)プランク長になりますが、これに比べても1.744×1019倍 = 1700京倍ほど大きい値です。
那由他とか京なんて単位が出てきたんでついでに日本語で表せる一番大きな数といえば9999無量大数9999不可思議9999那由他9999阿僧祇9999恒河沙9999極9999載9999正9999澗9999溝9999穣9999𥝱9999垓9999京9999兆9999億9999万9999 = 1072-1 ですが(これにも色々流儀があるようですが)それよりも9億4千倍ほど大きい値です。
もう本当にすごくすご~~~~~~~く大きな数です。
とはいっても大きさ比べを始めたらWeb上には10100や10200にチャレンジしてる人もいたりするので、それこそ四天王どころかザコもザコでしょう。
しかしPythonを使って普通のノートパソコン上で試行錯誤しつつ2週間程度でちょこちょことやった結果とすれば、わりと頑張ってるのではないでしょうか?
まあともかく何よりも楽しかったんでそれでよしにしましょう。
というわけでPyQtやマンデルブロ集合へのチャレンジはこのへんで終わりにしたいと思います。
次回は最後のまとめとして、そもそもの表題が「PyQtでお手軽GUI開発♪―――は可能だったか?」などという疑問文になっていたわけですが、それに対する自分なりの答えを出してみたいと思います。
- なお、何か間違いなどがありましたらこちらの方にコメントしてください(質問等でも構いませんが、多分答える能力があまりないのではないかと思います)