|
電卓とコンピューターの違い | ||||||||||||
|
この章では最も基本的な疑問である「コンピューターとは何か?」ということに関して説明します。 さて、コンピューターとはよく「電子計算機」と訳されます。それではコンピューターでない今までの「計算機」たとえば算盤とか計算尺とか手回し計算機(これを見たことのある人は相当ご年輩のはずです)とか電卓とはいったいどこが違うのでしょう? ちょっと青春の気分にそれではちょっと昔に戻って、二次方程式のことを思い出してください。 え?思い出すのもいやだって?困りましたね。もしコンピューターのことをある程度理解しようと思ったら、中学から高校1年程度の数学の素養がどうしても必要になります。 といってもどうしてもイヤだという人に無理強いする気はありません。今まで何千年も人はコンピューターなしで生きてきたのですから。はっきり言って、そういう生き方の方が人は幸せかもしれないですしね。(→私もそう思う) 以後は少し我慢してでもコンピューターのことを知りたい人向けです。でも大した数式は出てきませんから安心してください。 さて、二次方程式とは以下のような式を満たすχを求めなさいという問題です。中学校で習ったはずです(旧制中学ではどうだったかは知りませんが)
上の式で、a,b,cがたとえば3,4,−1であったとすれば以下のようになります。
さてここで忘れているかもしれませんが、二次方程式には有名な解の公式というのがあります。 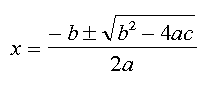 これが便利なのはこの式さえ覚えておけば、式の中のA,B,Cを上の例ならば3,4,−1とそれぞれ置き換えれば答えが出てしまう点にあります。 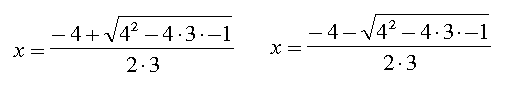 では上の式を電卓で計算してみましょう。ここで使う電卓は、ウィンドウズのおまけについているような、四則演算(+−×÷)と平方根(ルート)と簡単なメモリー機能があるだけとします。 そのためにはだいたい以下のようにキーを押す必要があるでしょう。以下の例はウィンドウズにおまけで付いてくる電卓ソフトを元にしています。
やる気が失せてきますね。こんな問題が100題出されたとしたら、ほとんど拷問です。 もっとも正しい選択は、そんな羽目に陥らないようにすることなのですが・・・ 拷問されてしまった場合人生、運が悪いことはよくあります。上のような無理難題を吹っかけられても、逃げられないようなこともあるでしょう。ともかく生きていく以上は、文句を言っても始まらない状況はたくさんあります。そんな場合はどうしたらいいのでしょう? いかに楽をするかという課題は、人類の進化の原動力です。獲物を解体するためには、歯で食いちぎるよりは石器を使った方が楽でしょう。苦労して歩き回って獲物を狩るよりも、動物を飼育して増やした方が楽でしょう。銃剣で一人一人刺し殺すよりも、核爆弾を使った方がとっても楽です。 すなわち、ここであきらめてせこせこと計算を始めては、私たちの先祖に申し訳が立ちません。 ではどういう方法があるのでしょうか? まず考えられるのは奴隷を使うことです。少々抜けていても我慢強い人を言いなりにできれば、それに越したことはありません。 しかしそのためには懐柔したり弱みを握って脅したりといった不断の努力が必要です。しかも奴隷は時々反乱したりします。その上、人間ではいざというときあまりあてにはなりません。かといってほかの動物ではもっと大変です。 だとすれば残る道は、そういう機械を作る方法しかありません。でもそんなことができるのでしょうか?(できてるんですが) 答えはこうです。 あなたが例の二次方程式100問を解き始めたとします。すると何問も解かないうちに、数値だけは変わっているが、やり方そのものは全く同じことに気がつくはずです。 そこである人が計算機にこの計算のやり方を覚えさせることができないだろうか?と考えたわけです。そうすれば人はデータを入力するだけで良く、後は機械が勝手に計算してくれると。そう考えた人はフォン・ノイマンという人でした。 このフォン・ノイマンという人は天才だったので、本当にそういう機械を作ってしまいました(ただし彼の暗算能力は作った機械を越えていたという話ですが) 時は二次大戦のさなか、できた機械の名前は「ENIAC」といいました。この機械は部屋いっぱいの真空管でできていて、一秒間に3000回の足し算ができたといいます。彼らはその機械を使って大砲の弾の弾道計算をしました。 この機械が一昔前にはコンピューターの元祖だと言われていました。なぜ一昔前かというと「いや実はABCマシンこそが真の元祖だ」とか「実はバベッジの解析機関までさかのぼる」とか主張する人が現れて、現在おおもめにもめている最中だからです。どうでもいいことですけどね。 コンピューターソフトなければ・・・以上、何が言いたかったかというと、要するに 「コンピューター」とは計算の手順を覚えておくことができる計算機 なのです。 もう少し具体的に言うと、コンピューターとは以下のような動作をする計算機です。
ここで重要な点は、1の計算の手順で、違った手順を入れておけば、コンピューターは全く違った動作をするということです。 コンピューターは二次方程式を解く手順を入れておけば二次方程式を解きますが、代わりに連立方程式を解く手順を入れておけば、連立方程式が解けます。そのほか統計計算でも何でも、計算手順を交換することでできるようになるのです。 この「計算の手順」のことを「プログラム」といい、「プログラム」と「データ」をひっくるめて「コンピューターのソフトウェア」といいます。 さて、上のような動作をさせるためには計算機には少なくとも以下のような部品が必要です。
これらをひっくるめて「コンピューターのハードウェア」と言います。 ここまでくれば「コンピューター、ソフトなければただの箱」ということわざの意味はもうおわかりでしょう。ソフトウェアを入れ替えることでコンピューターは様々な動作をしますが、逆に言えばソフトウェアがなければコンピューターは何もできないのです。 コンピューターは算盤の成り上がりか?さてここまでコンピューターは計算機だと表現してきました。しかし普通の人はコンピューターをあまり計算には使っていないのではないでしょうか。 たぶんほとんどの人はワープロで文書を作ったり、ゲームをしたり、インターネットでHな画像を集めたりするのに使っているだけのはずです。 実際、二次方程式のような「計算」しかできないのであれば、コンピューターの用途は非常に限られたものでしかありません。それでは元が算盤の成り上がりのような物が、どうしてワープロに化けることができるのでしょうか? それはコンピューターにメモリーがあって、それにいろいろなデータを書いたり読んだりできることにあるのです。 書いたり読んだりできるというのはどういうことでしょう?これは、メモリーの好きな場所にデータを書き込むことができるし、好きな場所のデータを読むことができるということです。当たり前ですね。この程度のことができなければ困るのはわかるでしょう。 さてそれではメモリーのある場所に以下のような数字列が書いてあったとします。
この数字列に以下のような操作(読んで書くだけです)をします。 1)真ん中の456を読み出して、適当な場所にその値を書き込む。
2)789を読み出して元の456の場所に書き込む。
3)元の789の場所を空にする。
4)後ろの456を読み出して元の789のあった場所に書き込む
これは何でしょう?操作1〜3をワンセットで考えれば、ワープロなどでよくあるカットとか切り取りと言われる操作そっくりです。同様に操作4はペーストとか張り付けと言われる操作そっくりです。 実はあの操作は内部的にはほとんどこれと同じようなやりかたをしているのです。 これが可能ならば、同じように挿入・削除や検索・置換なんかもできそうだと思うでしょう。 コンピューターがワープロになれる最大の理由は、このようにコンピューターがメモリー操作をする機能を持っているからに他なりません。 コンピューターが今までの計算機以上の機能を持てるのは、ほとんどこの点に尽きます。このメモリー操作ができるために、コンピューターはほとんど無限に近い可能性をもっているのです。 果てしなき野望かくしてうまくソフトウェアを作ってやれば、コンピューターは非常に多彩な動作をすることができるのです。そこから極論、 コンピューターはなんでもできる!でもこれは嘘です。信じてはいけません。 なぜ嘘なのか、それが今後の重要なテーマになってきます。 |