|
2020/5/10(日) (雨)
[健康] |
|
新型コロナを占ってみる(5) 新規感染者数は減りつつあるが、思ったほど減ってないということで、予定通り5月末まで延長。 発表内容として、結局たいした中身が無かったのでまた改めて考えることにします。 そもそも日本はどこに向かおうとしているのか。 都会では病院がひっ迫して、ほぼ限界というのを伝え聞くので、病床数がどうなっているかを加味してみます。 新型コロナ対策病床数 26,187床。日本の人口1億2000万人で割ると、全国平均で1.82床/1万人。 5万人都市の場合、使える病床は1.82×5=9.1床。 病床上限値(青線)をグラフに書き込むと、 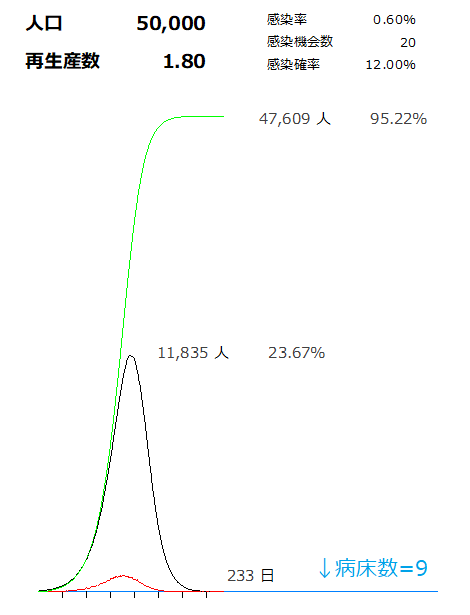 「ここまでなら感染者が増えていい」という余裕幅が見えません。 ちなみに、日本の急性期医療病床数は84床/1万人ほどですが、その線を引いたとしてもグラフは全く変わりません。 このグラフ自体は再生産数=1.8で推移したグラフなので、ピーク時には11,835人(人口の23.6%)もの感染者が出ているという結果を示しているので、すべての病床を新型コロナ用に転用しても全く収容できません。 「感染者数をコントロールして集団免疫を形成すれば」という作戦は到底無理です。 仮に感染者数をうまくコントロールできたとしましょう。 1人の感染者が病室を15日間占有すると仮定して、5万人が都合よく順に感染した場合、ベッドが1個しか使えないとき、すべての人が感染し切るまで15日×5万人=2000年。ベッドは9床使えるので、効率よく回せば期間を1/9にできますから、228年で全員に免疫がつくことになります。 その前に寿命で死んでますがな、という結果。 実効再生産数<1 を維持するしか生き残る道はありません。 実際に現状では実効再生産数が1を下回っているようなので、以後、グラフの縦軸を25倍にして検討してみたいと思います。 先ほどと同じグラフ(縦軸25倍版)。 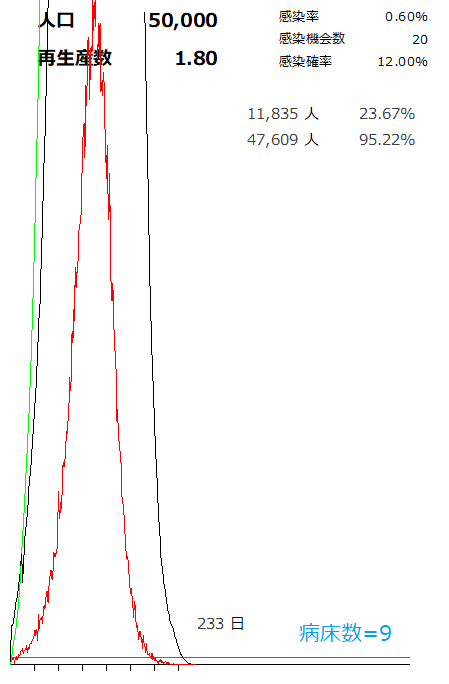 |
|
2020/4/27(月) (快晴)
[健康] |
|
新型コロナを占ってみる(4) コミュニティの大きさでどう収束するかの差を見てみました。 乱数でシミュレートしているので3回試行した結果です。 1万人都市に500人の感染者を作った場合 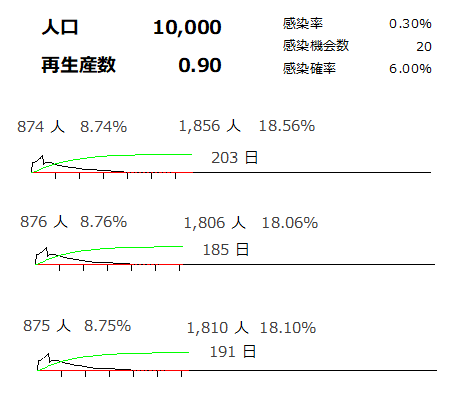 5万人都市に500人の感染者を作った場合 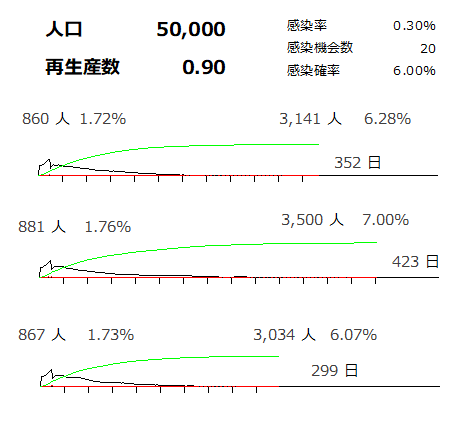 都市の大きさが大きいほど収束しにくいことがわかります。 GWの帰省という「コミュニティの大きさを広めてしまう行為」が収束を遅らせることを示唆しています。 |
|
2020/4/26(日) (曇り)
[健康] |
|
新型コロナを占ってみる(3) もう少し抑制して、再生産数を1.1程度まで抑えてみます。 累計感染者数は27%に抑えられますが、収束に3年かかります。 再生産数が1に近づくほど、ピークが低くなり、感染者数も少なくなる一方、収束に途方もない期間がかかることになります。 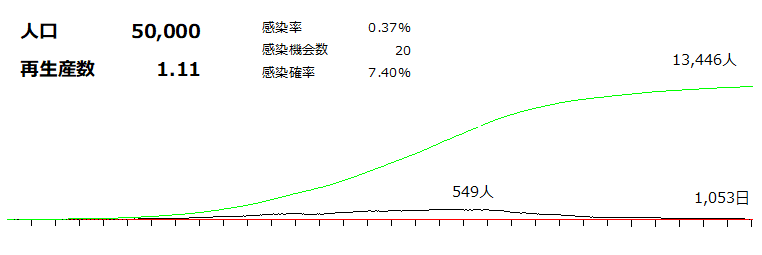 さらに抑えて再生産数が0.9になるようにすると、速攻で収束が始まります。 初期感染者数を10人として開始しているので、そのまま収束してグラフにならなくなります。 累計感染者数が43人、ピーク時の感染者数が14人というレベルで収束してしまいます。  再生産数が1を下回っている状態の外出自粛でどこまで抑え込めるか。 感染者500人を作ってシミュレーションしてみると 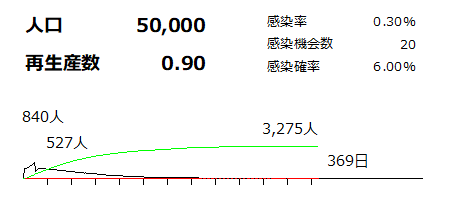 という結果。 500人という大量の感染者を解き放ったわりに感染力が無いので、次の人に感染できなかった感染者が一気に完治してガクっとピークダウンし、あとはダラダラと感染者が減っていきます。 もちろん、元の感染者数が少ないほど短い期間で収束します。 |
|
2020/4/23(木) (曇り)
[健康] |
|
新型コロナを占ってみる(2) 先日の10万人のシミュレーショングラフはプログラムの精度上の問題で正しく描画できてませんでした。 10万人規模の方が切りがいいのですが、最大5万人規模で勘弁してください。 日本人はハグ、キス、握手は滅多にやらず、土足で家に入らず、マスクが大好きなので再生産数が2.9なんていう数字にならないはずなので、ひとまず再生産数を半分に落としてみます。 黒の線が感染中の人数、赤の線が新規感染者数、緑の線が累計で、累計だけ高さを半分に圧縮しています。 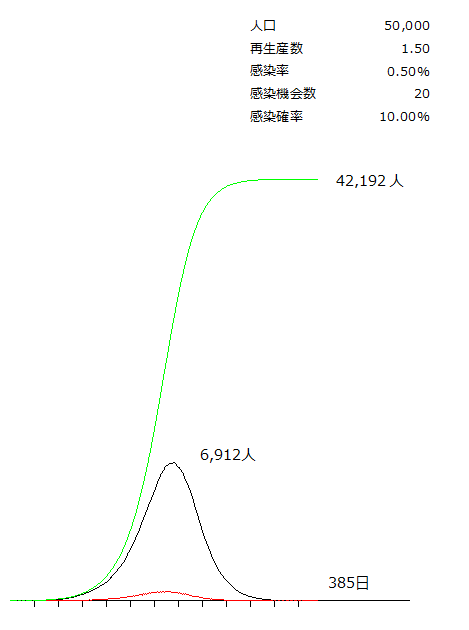 グラフのスケールは昨日と変えていないので、だいぶピークが抑えられていることがわかります。 それでも最終的に人口の8割にまで感染が広まり、ピーク時の感染者数は7000人(人口の14%)近く、収束に1年以上かかっています。 もう少し抑止して、再生産数を1.2まで落としてみます。 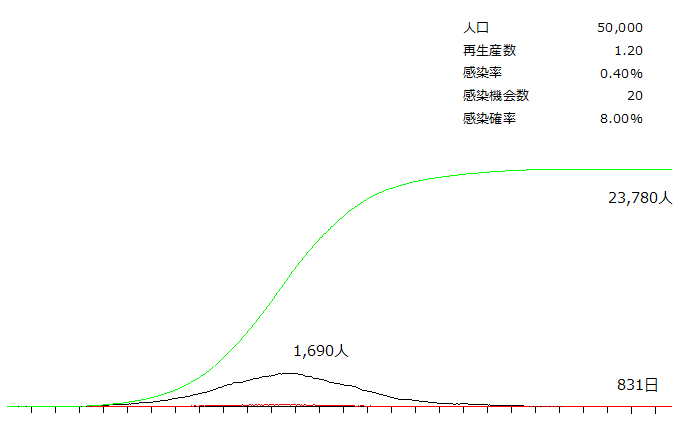 感染は人口の5割で食い止められ、ピーク時の感染者数も1700人程度と低くなりました。ただ、収束に2年程度費やすことになります。 乱数でシミュレーションしているので、毎回結果が微妙に変わるのですが傾向としてはだいたい同じになります。 |
|
2020/4/22(水) (曇り)
[健康] |
|
新型コロナを占ってみる 最近の話題は、新型コロナウイルス。 緊急事態宣言が5月6日に解除されるのかどうか、シミュレーションで考察してみたいと思います。 いろいろなシミュレーションモデルがあるそうですが、「ものすごくざっくり」やってみたいと思います。 感染してから発症するまでの潜伏期間は5-6日、発症前から感染力を持つと言われているので、感染5日目から感染させることができるとします。 完治基準がいまだにハッキリしませんが、2週間が目安になっているので、潜伏期間と合わせて完治まで20日かかることとします。つまり、5日目から19日目まで感染する力を持ち続けます。 シミュレーションですので、20日目でキッチリ完治します。 所定の人口の閉鎖都市を想定して、その中に10人の感染者を送り込みます。 それぞれの人は、1日に20人の人とランダムに接触し、所定の確率で感染が起きることとします。感染者となった人は4日の潜伏期間を経て感染する能力を持ち、またランダムに20人に接触して、一定の確率で感染させていきます。 完治した人は免疫を獲得するので、以後感染することはありません。 つまり、感染者がランダムに接触する人の中に免疫獲得者がいた場合、感染しません。 というだけのモデルです。 感染の能力を示す値には再生産数という値があり、1人の感染者が何人に感染させるかを示すパラメータです。 WHOの調べでは新型コロナウイルスの基本再生産数は2.9人とされています。 このシミュレーションでの再生産数は、20人×1%×15日=3.0人、という値になります。 とりあえず、無対策で放置した場合のシミュレーション結果から得られた感染者数推移をグラフを描いてみました。 人口が5万人の場合。 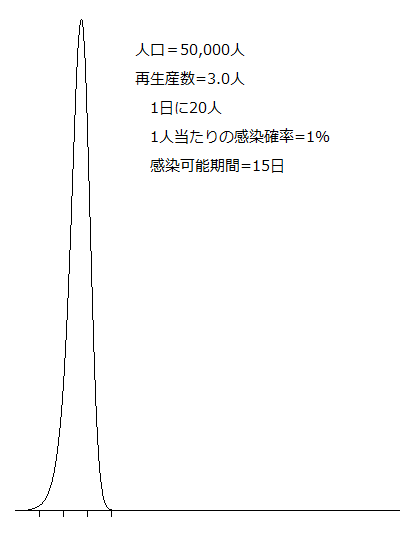 こちらが10万人の場合。 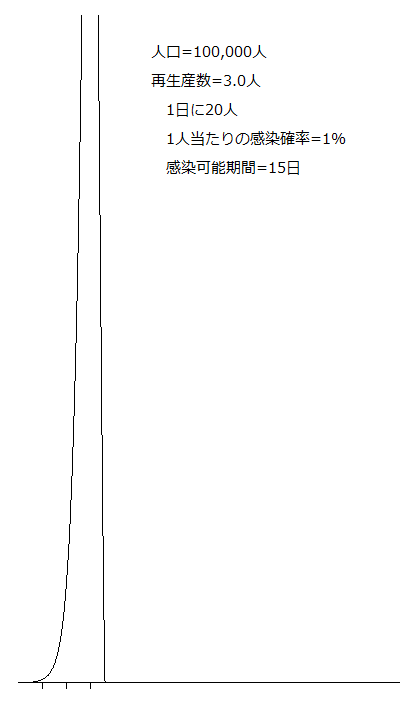 下の目盛りは30日ピッチなので、人口問わず、だいたい4か月で収束することになります。ただ、非常に鋭いピークを持つので、病院は確実にパンクします。 今日はここまで。 |
|
2020/4/20(月) |
|
-本日の更新- ・SXP2赤道儀 レビュー(4/20) Update |
|
2020/4/20(月) (雨)
[天文一般] |
|
復活 ざっくり2年ぐらい放置してましたが、復活することにしました。 あ、いや、SXP2を買ったもので。 機材も変わってきたのでレビューしつつ。 |