|
���@�藝�����̗D���_�� ��� �n粁@�� �����ٌc�ˍ��Z�E���ԍu�t �Q�O�O�Q�N�P���P�Q�A�P�R�� ���������Z�T�[�N������E�V�N��E��� |
���ӎ�
�@�@���@�藝������X�����Ă���`�Œ�N�����̂̓��M�I�����^�k�X�ł���ƁA�e�E�J�W�����Ȃǂ������Ă���B�O���o�ٍ̐e�w���@�藝�����̗D���_���x�ł́A���M�I�����^�k�X�́w�O�p�@�S���x�ɂ́A���@�藝��������Ȃ����Ƃ��q�ׂ��B����ł́A�������ꂪ����𐬂����̂��낤���B
�@�����H��̎R���i�搶�ɁA���M�I�����^�k�X�Ƃ��̌�̉��@�藝�̕��������u�������Ƃ���
�`�@Source�@Book�@in�@Mathematicsby�@David�@Eugene�@Smith�ADOVER�@PUBLICATIONS
INC.�@NEW�@YORK�@1959�@�G�i������w���w���T�x�ƌĂԁj���Љ�ꂽ�B
�@���̖{��ㆂ��Ă���ƁA�N�����B�E�X�ƃs�e�B�X�N�X��Prosthaphaeresis�u�����@�v�Ƃ����͂�����A���̒��ʼn��@�藝���̂��̂ł͂Ȃ��A���̉��p�Ƃ��āA
cos(�`�|�a)�|cos(�`�{�a)=2sin�`sin�a
����
sin�`sin�a��1/2[cos(�`�|�a)�|cos(�`�{�a)]
��p���āA���ӂ̐ς��E�ӂ̉��@�E���@�œ�����@���L�ڂ���Ă����B�܂�A�ނ�̖��ӎ��́A��@�����@�E���@�Ő��s���邱�Ƃɂ������B����́A�l�C�s�A�ɂ��ΐ��̔����O��̗��j�I�o�����ł������B
�@�N�����B�E�X�����@�藝���ؖ����Ă���}�́A���݉�X���ڂɂ��Ă���}�ɋ߂��B�ȉ����̗v�_�������L����
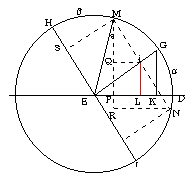 �ڂf�d�c�����A�ڂl�d�g�����@�Ƃ���B
�ڂf�d�c�����A�ڂl�d�g�����@�Ƃ���B
�@���f�d�j�䁢���d�k�@����@�f�d�F�f�j�����d�F���k�@����@�@
�f�d�́A���a�ł�����P����B�f�j��sin���A���d���l�r��sin��
�@�́A�P�Fsin����sin���F���k�@����@�A
�@�l�C�m�́A�d�f�Ɋւ��đΏ̂Ƃ���ƁA
�@�l�������m�A�l�m���Q�l��
���l�q�m�䁢�l�p���@
�@�䂦�ɁA�l�p�F�l�q���l���F�l�m
���Ȃ킿�A�l�p�F�l�q���P�F�Q�@������A�l�p��1/2 �l�q�A���������āA�@�l�p���p�q
�@�l�����o�q�@�ƂȂ�悤�ȓ_�����l�o��ɂƂ�B
�l�p�|�l�����p�q�|�l���A������A�l�p�|�l�����p�q�|�o�q�A���Ȃ킿�@���p���p�o
�p�o��1/2 ���o��1/2(�l�o�|�l���j��1/2(�l�o�|�o�q�j�A
���k���p�o��1/2(�l�o�|�o�q�j����@�B
�Ƃ���ŁA�l�o��sin�l�c��sin(�l�f�{�f�c)��sin(90���|�g�l�{�f�c)��sin(90���|���{��)
�@�@�@�@�@�@�@��sin(90���|���|��)��cos(���|���j��cos(���|��)
�@�@�@�@�@�o�q��sin�c�m��sin(90���|�f�c�|�m�h)��sin(90���|���|��)��cos(���{���j
�B�́A���k��1/2 [cos(���|��)�|cos(���{��)]�]���āA�A��
�P�Fsin����sin���F1/2 [cos(���|��)�|cos(���{��)]
������Asin��sin����1/2 [cos(���|��)�|cos(���{��)]
�@�ȏ�̂悤�ɁA�N�����B�E�X�́A�Ώ́A�����A��Ꭾ��p���ē����Ă��āA�Ñ�̕����̍������邪�A���a���P�Ƃ���P�ʉ~�����Ă��邱�Ƃ́A����I�ł���B
�@�ނ��ӎ������̂́A���@�藝�ł͂Ȃ��āA�v�Z�p�Ƃ��āA�O�p���𗘗p���邱�Ƃł������B�]���āAcos(���{���j���H�A�Ȃǂ̈ӎ��͖��������悤�Ɍ�����B
�@����̉�X�́A�ȒP�ɗ]����p���邪�A�ނ́A�]�p�̐����A�܂��͗]�ʂ̐����Ƃ��Ă���B���������I���A���邢�́A��̊��\�������ɂ��]���ɂ������Ɏg���邱�ƂŖ������Ă����Ǝv����B
�@�t�����A���E�J�W�����w�������w�j�x���q���V���E��o����ɂ��A���M�I�����^�k�X�́A(1436�`1476�j�P�[�j�X�u���O�ɏZ�ݔӔN���[�}���c�ɏ�����ă��[�}�ɕ��������Ő��U������B
���M�I�����^�k�X���a�S�N��ɁA�N���X�g�b�t�F���E�N�����B�E�X(1537�`1612)�W�F�X�E�B�g���̑m�����o�����A���㐏��̐��w�҂Ə̂���ꂽ�B�s�`�X�N�X(1561�`1613)�́A�h�C�c�̖q�t�Ő��w�҂Ƃ��ėD��A�O�p�@�̋��ȏ��������Ă���Ƃ���B
�@��L�ŏЉ���ؖ��́A1593�N���[�}�ŏo�ł��ꂽ�A�N�����B�E�X�̒���w�A�X�g�����r�E���x�ɋL�ڂ���Ă���Ƃ����B�iastro���A�V���A�{labium���ꁁastrolabium�V���p�ꎫ�T�j
�@�ȉ��́A�n粂��w���w���T�x�̓��Y����PP�D455�`462����{��ɖ|�����̂ł���B���̍ۂɁA���T�̌���������Ă������B
�@�w���w���T�x�̍\���́A���e����i�܂��͉p��ȊO�̌���j����p��ɖ|�����҂̉���������āA���p�����ׂ��{���������A���O�ɒ��҂̒�������B
�N�����B�E�X�@�Ɓ@�s�`�X�N�X
�u�����@�v�ɂ����i�n粒��j
�i���e���ꂩ��̖�̓j���[���[�N�s�C�F�V���@��w�A�W���N�e�B�[���E�M���X�u���O�����ɂ��B�j
�@�ΐ��̔������ߎ����ɁA���w�ҒB�́A�揜�������ɒu��������u�����@�v�ƌĂ����@��p���Ă����B���̕��@�́A���̌����Ɋ�Â��Ă����B
cos(�`�|�a)�|cos(�`�{�a)=2sin�`sin�a
�j�R���E�X�E���C�}���X�E�E���X�X�E�f�B�g�}���X�X�́A���ʎO�p�̉�@�ł�����g���Ă����B�����ł́A���a�A�@�@sin�`�Asin�a�ɑ��đ�l�̔䗦�����߂邽�߂ɕK�v�ł������B�N���X�g�t�@�[�E�N�����B�E�X(1537�|1612)�́A���̕��@�𐳊��Ɛ��ڂɂ܂Ŕ��W�������B���ہA�ނ́A�C�ӂ̓̐ς̋��ߕ������̕��@�Ɉ˂��Ď������B����́A�ΐ��̌�����\��������̂ł������B
�@�ȉ���o�̑����p�ӏ��ł́A�N�����B�E�X���A��̐����̐ς��u�����@�v�����ŋ��߂����@�������Ă���B����́A���C�}���X�E�E���X�X�����������̌����i�ؼ��٥��ݼ�فj�������Ă���悤���B��v�f�̂��ꂼ�ꂪ���a��菬�����Ƃ��̂݁A���̔��a������ʂ̐����ƌ��Ȃ����A���̕��������p�\�ł���B
�@�����p�ӏ��ɂ́A�N�����B�E�X�́A�ꐔ�����a���傫�����̏ꍇ�ɂ܂ŁA�i�W���������@�������Ă���B
�@���҂́A�w�A�X�g�����r�E���x�i���[�}�A1593�j�A�ꊪ�A�����}53�ɂ���B
�����p�ӏ�
�@��Ƃ��āA�i������́j��O�{17��45���̐Ԉ��i�P�j�����߂��������Ă݂�B���a�u�ő�Ԉ܁v�i�Q�j�́A�^����ꂽ�����_�̋߂��̓_����̋����̐����Γ����_�̐Ԉ܂̐����ɓ������B�i�R�j
|
|
�i�n粒��j�m�@prosthaphaeresis�́A�n�d�c�ɂ��A�M���V����R���̃��e����ŁA�V���w�p��A�����A�@�ꌹ�́A
�@�@�@�σ̓ЃƃÁi�ˁjbefore�{���Ӄ��ǃσÃЃǃ�subtraction�@�Ƃ���B
�������A����ł́A�u�O�Ɉ������Ɓv�A�u�O���@�v�A�u�挸�@�v�ƂȂ�A�Ӗ��s���ɂȂ�B�@The
Pocket Oxford Greek Dictionary�i�I�b�N�X�t�H�[�h�E�M���V���ꎫ�T�j�ɂ��ƁA�σ̓ЃƃÃЃǃЂ́A������addition�A������Ӄ��ǃσÃЃǃЂ́A������taking
away�Asubtraction�Aabstraction�@�Ƃ���B���������āA���̓�̖�������������ƁA�σ̓ЃƃÃЃǃЁ{���Ӄ��ǃσÃЃǃЁ��σ̓Ѓ����Ӄ��ǃσÃЃǃ�
������u�����@�v�Ƃ��Ă������B]
��(1)�G�Ԉ܂́A�V����̓_����ԓ��܂ł̋����ł���B�i�����͂������q�ߐ��ɉ����đ�����B�j
�@17��45���́A�����P�Q�{�̑�O�{�̓_�ł���B�����P�Q�{�̊e�{��30�x���ł���A���{�͐ԓ��Ɖ����Ƃ̌�_����n�܂�̂ŁA��_���炻�̓_�܂ł̋����́A30���{30���{17��45����77��45���ɓ������B ��(�Q)�G�ԓ��Ɖ����Ō`�Â�����p�x�B[����I�\���ł́A�u�����X�Ίp�v�i�n粒��j] �@�����ŁA�u�����@�v�ɂ��ƁA �]�p�Ə��������̌ʂ̘a�G35��45���B���̐����G3842497 �]�p�Ə��������̌ʂ̍��G11��15���B���̐����G1950903 �����̘a�G�@�@7793400 ��̘a�̔����G3896700�B�Ԉ�22��56���i�S�j ��(�R)�G �`�a��ԓ��̌ʂƂ���B�`�b�������̌ʂƂ���B�`�́A�ŋߓ_�i�t���_���H���_[�n粒�]�j�|�|�|�����ԓ��Ɖ����Ƃ̌�_�|�|�|�b��������O�{�̓_�ł���B�_����̋����`�b�́A�Q�{���{17��45������77��45���ł���B�ԓ�����b�_�܂ł̋����b�a�́A�q�ߐ��ɉ����đ�����B�b�a���`�a�̐����ł���A�O�p�`�`�a�b�́A���p���ʎO�p�`�ł��邱�Ƃ��킩��B�����ŁA���̎���B sin�a�Fsin�`��sin�`�b�Fsin�b�a �����ŁA sin�a��sin90�����P(���a�j�A�`��23��30�� �ł���B�i����́A�ԓ��Ɖ����Ƃ̊p�Ƃ��Ēm���Ă���B[�u�����X�Ίp�v�i�n粒��j]�j sin�`�b��sin77��45���A�ł���A�b�a���v�Z�����ׂ��ʂł���B�����ŁA����I�\�L�ɏ]���A�@ �@�@�@�P�Fsin23��30����sin77��45���Fsin�b�a �ƂȂ�A�u�����@�v�K���Ɋ����Ă���B ��(�S)�G�����B�N�����B�E�X�ɂ���ďؖ����ꂽ�藝�ɏ]���A �@�@�@�P�Fsin�`��sin�a�F1/2[sin(90���|�`�{�a�j�|sin(90���|�`�|�a)]�@�@�@ �����ŁA�`��77��45���A90���|�`��12��15���A�a��23��30���G �@�@�@�@90���|�`�{�a��23��30���{12��15����35��45�� �@�@90���|�`�|�a��23��30���|12��15����11��15�� sin(90���|�`�{�a�j��sin(90���|�`�|�a)�́A90���|�`���a���傫�������������ɂ���āA������ꂽ��܂��́A�����ꂽ�肳���B�䂦�ɁA���߂�ׂ��ς́A �@�@�@sin23��30���~sin77��45����1/2sin35��45���|1/2sin11��15�� �����p�ӏ� �@���a�Ɣ��a��菬�������Ƃ̔�́A���a�����傫�����Ƌ��߂�ׂ����̔�ɓ������Ƃ��A�� �@���̂悤�ɂ��ē���ꂽ��l�̔䗦�ɁA��L���@�̏��Ə��������̐��Ƃ̐ς���������B(5�j ��(�T)�G�����Ƃ��āA�N�����B�E�X�́A3,912,247�~11,917,537��A�@10�V�F391,247��11,917,535�F���A �̑�O��11,917,535��10�V���傫���ƌ��Ȃ��Ă���B�����10�V�Ŋ���ƁA���͂P�ŁA�]�肪1,917,535�ł���B�N�����B�E�X�́A�⏕��Ꭾ�A�@�@�@10�V�F391,247��11,917,535�F���A���l���Ă���B �\����A391,247��sin23���Q���A1,917,535��sin11��3���������Ă���B�����ŁA�䗦�́A���̂悤�ɂȂ�B �@�@�@10�V�Fsin23��2����sin11��3���F���@�@�ނ́A�ȏ�̂悤�ɐi�߂āA �@�@�@10�V�Fsin23��2����sin11��3���F1/2[sin(90���|23��2���{11��3��)�|sin(90���|23��2���|11��3��)]�@����́A�����ɓ������B �@�@�@10�V�Fsin23��2����sin11��3���F1/2[sin78��1���|sin55��55��] ����ɂ��A����749,923�@�ƂȂ�B ���̌��ʂɁA���391,247�~���P��������B �s�`�X�N�X�u�����@�v�ɂ����i�U�j �@���P�B�O�����m���Ă����Ꭾ���^������B��ꍀ�����a�ł���A��A��O���������ł���B��@�A���@������āA���̔�Ꭾ�������B �@�����ɑΉ�����ʂ̗]�p�̍��v���Ƃ�ƁA���p���ʎO�p�`��B���ʎO�p�`�̑�l�̗�ɓK�����Ă��āA�u�����@�v�݂̂ʼn������Ƃ��ł���B �@�@�@�@�@���a�`�d�Fsin�d�e��sin�`�d�Fsin�a�b ��A��O�����̌ʂ`�d�A�ʂd�e�ɑ���]�ʂd�c�A�]�ʂa�d�����߂�ƁA�O�p�`�a�d�c��B���̎O�p�`�͂d�����p�ł���B���߂�ׂ��ʂa�b�́A�ӂc�a�̗]�ʂł���B���ʎO�p�ɂ��Ă̑�l�����ɂ���āA�揜�Ȃ��ɂ�������߂邱�Ƃ��ł���B �@�ӂ`�a��42���Ƃ��A�d�e��48��25���Ƃ���A�a�d��48���A�c�d��41��35���@�ł���A�ȉ��̂悤�ɎZ�o����B �@�@�@�@�c�d��41��35���@��41��35���@ �a�d��48���F�]�p�G42�� �a89��35��83��35��sin�@�@9937354 ��0��25���@�@�@�@�@�@�@sin�@�@�@72721 �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�a�@10010075 ����5005037 ���ꂪ�A���߂�ׂ��ʂa�b�̐����Ȃ̂ŁA�a�b��36��2���ƂȂ�B �N�����B�E�X �O�p�@�ɉ��p�����u�����@�v�ɂ��� �i���e���ꂩ��̖�́A�j���[���[�N�s�A�C�F�V���@��w�A�ު�è�فE�M���X�u���O�����ɂ��j �@���̈��p�����́A�N���X�g�t�@�E�N�����B�E�X�w�A�X�g�����r�E���x�i���[�}�A1593�jpp.179�`180�D���̖{�ɂ́A�����̎��̏ؖ�������B cos(�`�|�a)�|cos(�`�{�a)���Qsin�`sin�a �N�����B�E�X�́A���̏ꍇ�ɕ����čl�@���Ă���B �@�@�@�@�@1)�@�`�{�a��90�� �@�@�@�@�@2)�@�`�{�a��90�� �@�@�@�@�@3)�@�`�{�a��90�� ���̏ꍇ�́A���̂悤�ɂȂ�B �@�@�@�@�@�@�@sin�Q�`���Qsin�`cos�` �N�����B�E�X�́A���̒藝�����̖��_���A�j�R���E�X�E���C�}���X�E�E���X�X�E�f�B�g�}���X�X�ɗ^���Ă���B�������A�`�E�u���I�E���~���[���w�O�p�@���j�u�`�xp.173�Ɉ˂�A��҂͓�̏ꍇ�A�������A��O�̏ꍇ�����ؖ����Ă��Ȃ��Ƃ����B������ɂ���A�N�����B�E�X�́A�藝�Əؖ������S�Ȍ`�Ō��ɂ����ŏ��̐l���ł���B �@�ނ̒��ɂ��A�N�����B�E�X�́A�u�����@�v�̓����Ƃ��āA���̒藝��p���Ă����B���̒�����A�l�C�s�A�ɂ��ΐ��̔��������邪�A���̒藝�́A���C�}���X�E�E���X�X��A�r�����M�A�N�����B�E�X�Ȃǂ̐��w�҂ɂ���āA�揜�������ɒu�������邽�߂ɗp�����Ă����B�ΐ��̗��_�ƁA���ꂪ�����łȂ��Ă��A�������̊W�͖��炩�ł���B��͈ȉ��B �⏕�藝�k�T�T�T�|�|�|�O�A�l�N�O�A�j�R���E�X�E���C�}���X�E�E���X�X�E�f�B�g�}���X�X�́A����̃��[�t���b�g���o�ł����B���̒��ŁA�u�����@�v������(1)�����̋��ʎO�p�`�������I���ȍH�v�������Ă���B�������A��Ꭾ�̒��ŁA������������S���A���a�����̈ʒu�ɂ���Ƃ��̂݁A���̕��@�͎g�p�\�ł���B�����ł́A����ʓI�Ȓ藝����낤�Ǝv���B����䂦�ɁA�����ɑ��Ă���łȂ��A���ځA�]�ځA�]���⑼�̐��ɑ��Ă��A�܂����a�����ʒu�ɗ��Ȃ���Ȃ�Ȃ��Ƃ������ƂłȂ��Ă��A���̒藝�͗L���ł���B���Ƃ��A���a���n�߂ɂ��낤�ƁA���I���ɂ��낤�Ƃ��A�^�ɂ��낤�Ƃ��A���ꂪ�S�R�Ȃ��Ă��A���̒藝���L���ł���B�����̎����́A�a�V�ŁA��тƖ����ɖ����Ă���B �@�藝�B�|�|�|���a�ΔC�ӂ̌ʂ̐����́A���̔C�ӂ̌ʂ̐���������̌ʂ��琬��ʂł���A���̗ʂ́u�����@�v��悤�Ɍ`�������B���������̐����A�傫�����̐��̗]�p�ɉ������A���v�̐��������߂���B�i�Q�j �䂦�ɁA �@�P�D�����A�����������傫�����̗]�p�ɓ������Ƃ��A�����A��̌ʂ����Ɏl���~�ɓ������Ƃ��A�v�Z���ꂽ�����̔�������Ꭾ�̋��߂�ׂ���l���ɂȂ�B�i�R�j �@�Q�D�������A���������������傫�����̗]�p��菬����������i����́A��̌ʂ̍��v���l���~�����������Ƃ��ɂ����邪�j�������ʂ͑傫�����̗]�p���猸�����A����ɂ���ĉ�������ȑO�̌ʊԂ̍���B���̍��̐������i�S�j�A�ȑO�ɋ��߂��������猸������B���̔��������߂�ׂ���Ꭾ�̑�l���ɂȂ�B�i�T�j �@�R�D�������A�������������̌ʂ��傫�����̗]�p���傫����A�i�����������Ƃ́A��̌ʂ̍��v���l���~�����傫���Ƃ��j�傫�����̗]�p���A�����������猸������B���̌��ʁA�ȑO�ɑ�������ʂ̍���B���v�̔�������Ꭾ�̒��ŋ��߂�ׂ���l���ł���B�i�U�j �@����́A��L���҂̒藝�ł���A�ȉ��̕��@�ŏؖ������B �@���̐}�ŁA�d�f�́A���a�ł���B����ɁA �@ �������ʂf�c�́A�傫�����̌ʂh�c�̗]�ʂł���i���邢�́A�����f�c���傫�����̌ʂł���h�c�����������Ȃ�A�h�c���c�h�ɂ��A�h�c�͑傫�����̌ʂf�c�̗]�ʂł��邪�j�A���߂�ׂ���Ꭾ��l���́A�o�p�ł���B����́A�ʂl�c�̐����l�o�̔����ɓ������B�ʂl�c�͌ʂc�f�Ƃf�l���琬��A�ʂg�l�̗]�ʂł���B �@���A��O�̐}�ŁA�d�f�͔��a�ŁA �@�@�d�f�F�f�j�i�ʂf�c�̐����j���d���i�ʂh�m�A�g�l�̐����j�F���k�i���̐����j ���}���̌ʂf�c�́A�ʂh�m�̗]�ʂf�m��菬�����̂ŁA�i�������R�ɁA�f�c���傫���āA�h�m���������Ƃ��A�h�m���ʂf�c�̗]�ʂ����������Ȃ�̂Łj�A���߂鐳���o�p�i������Ꭾ��l���j�́A�ȉ��̂悤�ɋ��߂�B ���c�m�̐����q�o(�l���ɓ������j�́A�l�o���������A���̌��ʂ��A�ʂc�f�ƌʂg�l�̗]�ʂf�l���琬��ʂl�c�̐����ł���B�����o�p�́A�o���̔����ɂȂ�B���x�p�q���l�q�̔����ł���̂Ɠ����ł���B�i�V�j �@�����A���ɂf�c���傫���A�h�m���������Ȃ�A�Ƃ������l�o���ʂl�a�̐����ɂȂ�B�ʂl�a�́A�ʂl�g�ƌʂf�c�̗]�ʂg�a���琬��B �@��O�}�ɂ����āA�h�m���f�c�̗]�ʂh�c���傫���̂ŁA�i�܂��́A�������ɁA�f�c���������A�h�m���傫���Ƃ��A�f�d���ʂh�m�̗]�ʂf�m��������ł��낤���j�A���߂�ׂ���Ꭾ��l���́A���m�c�̐����q�o�������ē�����B�����l�����q�o���l�o�ɉ�����B�l�o�́A�ʂl�a�̐����ł���B�ʂl�a�͌ʂg�l�ƌʂg�a����Ȃ�B�����o�p�́A�������o�̔����ł���i�Ȃ��Ȃ�p�q��1/2�l�q�j�A���߂�������k�ɓ������B �@�����A���ɁA�ʂf�c���������A�ʂh�m���傫����A�l�o�́A�Ƃ������ʂl�c�̐����ɂȂ�B�ʂl�c�́A�ʂf�c�ƌʂg�l�̗]�ʂf�l���琬��B ��(1)�@178�łŃN�����B�E�X�́A�u�����@�v�����@�ƌ��@�݂̂��p��������@�Ƃ��Ē�`���Ă���B��(2)�@�����ʂ��`�Ƃa�ł���Ȃ�A���̑���́Asin(90���|�a�{�`)���Ƃ鎖�Ɠ��l�ł���B ��(3)�@����́A����I�\�L�ł́A�@�P�Fsin�`��sin�a�F1/2
sin(90���|�a�{�`) �܂��́A�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�P�Fsin(90���|�a)��sin�a�F1/2
sin(90���|�a�{90���|�a) �ȒP�ɂ��ā@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�P�Fcos�a��sin�a�F1/2
sin�Q�a �����@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@sin�Q�a���Qsin�acos�a ��(4)�@�����Asin(90���|�`�|�a) ��(5)���̔�Ꭾ�́A���̌`�ł���B�@�@�@�@�P�Fsin�`��sin�a�F1/2[sin(90���|�`�{�a)�|sin(90���|�`�|�a) ����́A���̎��Ɠ��l�ł���B�@�@�@�@�@�@�@�P�Fsin�`��sin�a�F1/2[cos(�`�|�a)�|cos(�`�{�a) ��(6)�@����I�\�L�ł́A�����a��90���|�`�i�����@�`�{�a��90���j�Ȃ�A���@�̂�����ς���B �@�@�@(90���|�`)�|�a�̑���ɁA�a�|(90���|�`)�Ƃ���B ��(7)�@����I�L�@�ł́A �@�@�@�@�l�o��sin�l�c��sin(�c�f�{�f�l)��sin(�c�f�{90���|�g�l)��cos(�c�f�|�g�l) ����ɁA���l���p�䁢�l�m�q�@����@�l����1/2 �l�m�A�䂦�ɂp�q��1/2 �l�q
�O�̃y�[�W�ɖ߂��B�@�@�@�@�@�}�T���́@home�@page�@��
 ���̂悤�ɐi�߂�B���a���傫����O�̐��́A���a�ɂ���Ċ����Ȃ���Ȃ�Ȃ��B���́A�E���ŁA�V�̐������폜���ē����鐔�ł���B�����̂V�̐����́A�]��𐬂��B�䂦�ɁA�䗦�G���a�Ώ��Ȃ����A�]����߂鐔�A�́A�u�����@�v���K�p�����A�������������Ɨ]��̌ʂ������ƌ��Ȃ����Ƃ��A�\���瓾����B
���̂悤�ɐi�߂�B���a���傫����O�̐��́A���a�ɂ���Ċ����Ȃ���Ȃ�Ȃ��B���́A�E���ŁA�V�̐������폜���ē����鐔�ł���B�����̂V�̐����́A�]��𐬂��B�䂦�ɁA�䗦�G���a�Ώ��Ȃ����A�]����߂鐔�A�́A�u�����@�v���K�p�����A�������������Ɨ]��̌ʂ������ƌ��Ȃ����Ƃ��A�\���瓾����B �@�Ⴆ�A���̔�Ꭾ���^����ꂽ�Ƃ���B
�@�Ⴆ�A���̔�Ꭾ���^����ꂽ�Ƃ���B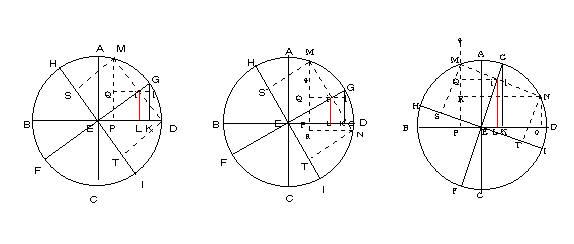 �@�d�f�F�f�j�i�ʂf�c�̐����j���d���i�ʂh�c�A�g�l�̐����j�F���k�i���̐����j
�@�d�f�F�f�j�i�ʂf�c�̐����j���d���i�ʂh�c�A�g�l�̐����j�F���k�i���̐����j