乽旝暘仼仺愊暘乿婍嶌惢偵偮偄偰
搉绮丂彑乮嶥杫嬚帡岺嬈崅峑乯
摴悢嫤崅峑僒乕僋儖侾寧椺夛
俀侽侽侾擭侾寧俋丆侾侽擔
嶥杫巗杒嬫丄偁偗傏偺椃娰
丂侾丏栤戣堄幆丟旝愊暘偑屳偄偵媡墘嶼偱偁傞偙偲傪帇妎偵慽偊傞桳岠側庤抜偑梸偟偄丏
丂俀丏侾俋俋俆擭慡崙嫵尋乮嶥杫乯敪昞丄旽桬堦愭惗乮嶉嬍擖娫岦梲崅峑乯偺
丂丂丂丂儗億乕僩亀拰忬僌儔僼偵傛傞旝暘丒愊暘朄偺巜摫亁偵巋寖傪庴偗偨丅
丂俁丏旽儗億乕僩偺奣梫偼師偺傛偆側傕偺偱偁傞丅丂
丂嘆丂娭悢偺僌儔僼傪拰忬偱昤偔丅僷僜僐儞墖梡丂
丂嘇丂嵎暘傪怓暘偗偟偰丄摨條偵拰忬僌儔僼偵昤偔丅旝暘學悢偺嬤帡抣偲偟偰偼廲幉曽岦偵弅彫偝傟傞丅丂丂
丂嘊丂廲幉曽岦偺弅彫傪夝彍偟偰拰忬僌儔僼偱昤偔丅偙傟偑摫娭悢偺拰忬僌儔僼偱偁傞丅丂丂
丂嘋丂摫娭悢偺僌儔僼傪拰忬偵昤偔丂丂
丂嘍丂廲幉曽岦偵弅彫偡傞丅嵎暘偑昞傟傞丅丂丂
丂嘐丂嵎暘傪弴師愊傒忋偘偰偄偔丅弌棃傞偺偑尨巒娭悢偱偁傞丅
丂係丏僷僜僐儞偵埶傜側偄偱捈愙栚偵尒偊傞嫵嬶傪嶌傞丅丂丂
丂丂丂嵽椏偼丄昞巻巻乮敿柺敀岤巻乯丄屝丄敀巺丄僒儔儞儔僢僾丄
丂丂丂摴嬶偼丄僇僢僞乕丄珲丄僗僥傿僾儔乕丄恓丄愮枃捠偟
丂俆丏弌棃忋偑傝丟惗棃偺晄婍梡偱墌妸偵摦偐側偄丅忋庤偵偮偔傟偽偆傑偔摦偔丅丂丂
丂丂丂偨偩偟丄摫娭悢偑尨娭悢偐傜嶻傒弌偝傟傞夁掱丄摫娭悢偑嵎暘偺嬌尷抣偱偁傞偙偲摫娭悢偐傜尨巒娭悢傪嶌傝偁偘傞夁掱偑傒偊傞丅
丂俇丏寚揰丟嵎暘偼旝暘學悢偦偺傕偺偱側偄丅摫娭悢偑弅彫偝傟傞丅丂丂丂丂
丂丂丂丂 丂丂
丂丂
丂丂僌儔僼偵弌偰偔傞偺偼儮倷丄儮倶亖0.1丂側偺偱丄廫暘偺堦偵弅彫偝傟傞丅
丂俈丏夵慞揰丟億僀儞僩偼丄抁嶜偺惛枾壔 嵽椏傪栘惢丄僾儔僗僠僢僋偵偟偰丄嬫暘傪傕偭偲彫偝偔偡傞丅丂丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂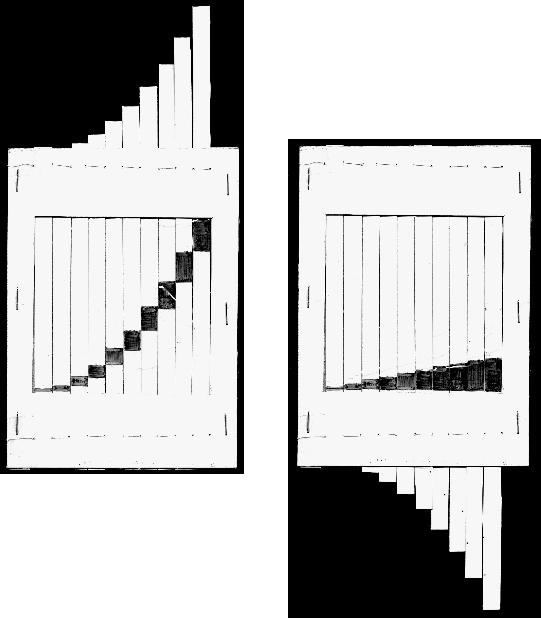 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂丂嵍偼丄擇師娭悢偺僌儔僼丄怓偑晅偄偰偄傞晹暘偼嵎暘丂丂丂丂丂
丂丂丂塃偼丄嵎暘偩偗傪暲傋偨傕偺丄偙傟偼丄摫娭悢傪昞偟偰偄傞丅
丂丂丂偨偩偟丄摫娭悢偺廲幉偼弅彫偝傟偰偄傞丅丂丂
丂丂丂塃偐傜嵍傪尒傞偲丄嵎暘傪愊傒廳偹偨偲偙傠丄懄偪愊暘偝傟偨忬懺傪昞偟偰偄傞丅
丂丂丂恾偺榞偐傜偼傒弌偰偄傞侾侽枃偺抁嶜傪摦偐偡偙偲偱旝暘偟偨傝丄愊暘偟偨傝偱偒傞丅
尦偵栠傞
儂乕儉儁乕僕偵栠傞
 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂