そこへ彼らと同じ部にいた、今は高校生になっている樺先輩が現れた。中学生の練習を見に母校にやってきていたのだ。　　　　　　　　　　　
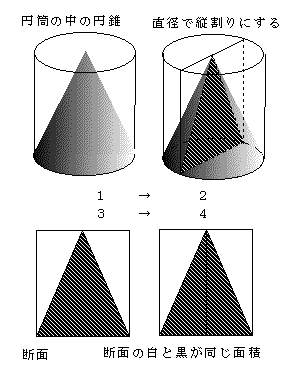
樺先輩「素男君のように縦割りでなくて横割りで考えられるよ。」
素男「どうやってですか？」
聡子「切る場所によって断面積が変わるのに、何か上手い手を考えたんですか？」
樺先輩「カヴァリエーリの法則というのでその問題は解けるよ。」
素男「河馬なんとかって何ですか？」
樺先輩「カヴァリエーリ！こんな図のように高さが同じ立体図形があって、同じ水準高の断面積が一方のｋ倍なら、体積もｋ倍になるという法則だよ。」
 

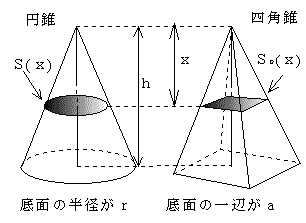聡子「ということは、最初に断面積の比を出して、次ぎに体積を出すときは、その比を使って一方の体積を他方の体積で表されるんですね。」
樺先輩「その通りだよ。二人で計算してみたらいいよ。」
素男と聡子は、樺先輩の手助けを得ながら下のように計算をした。

頂点から断面までの距離をｘ、円錐の断面積をＳ(ｘ)、四角錐の断面積をＳ０(ｘ) とする。断面積はｘに比例するから、円錐について、 　 これから　　四角錐について、 　これから　　円錐の体積をＶ、四角錐の体積をＶ０とすると、 カヴァリエーリの法則から、Ｖ：Ｖ０＝Ｓ：Ｓ０　即ち 式を簡略にして、 Ｖ：Ｖ０＝π２：ａ２　これより

素男「四角錐の体積Ｖ_０が分からないと、円錐の体積が分からないス」
聡子「四角錐の体積は”底面積掛ける高さ割る３”で出せるから、この場合、1/3ａ^２ｈだから、上の式に入れて、Ｖ＝1/3πｒ^２ｈ　となります。」
樺先輩「その通りだよ。聡子君は計算が正確だね。」
素男「先輩！僕は、円錐の体積を出すとき３で割ることが、納得できなかったのですが、今度は、四角錐の体積を出すときも３で割りますよね。どうして３分の１になるのですか？」
樺先輩「カヴァリエーリの考えを初めから言うと、鉛筆で定規に沿って線分を描くとするよ。一本描いては、定規平行にをすこしずらしてまた一本描くという具合に沢山描くとある図形ができるよね。」
聡子「平行線で出来た図形ですね。」
樺先輩「カヴァリエーリは、無数の平行線線分が面積をつくり、無数の平行平面分が体積をつくると考えたんだよ。」
素男「無数の線は引けるのかな？」
樺先輩「現実には引けないけど、引けるものとして考えるのさ」
素男「ちょっとインチキくさいスね。」
樺先輩「先ず面積だけど、正方形を対角線で分けると二つの二等辺直角三角形ができるけど、その面積が等しいことを、構成する平行線分が等しいからだと言ってるんだ」
素男「どうしてそうなるスか？」
樺先輩「ＢＣに平行なＰＱという線分をＢＣから初めてＡＤまでずらしながら線を引いていくとするよ。左のｘ′と等しい線分が右のｙに必ず現れる。逆に右のｙ′と同じ線分が左のｘに現れるので、線を引き終わったら結局同じ線分が等しく二つの三角形に在るので、面積が等しいということさ」
 

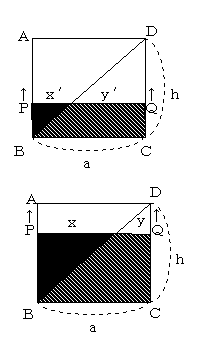素男「実際には線を引けないでないスか？」
樺先輩「そう、ＰＱを動かすことに主眼があって、ＰＱが動くとその後に無数の線が引かれたと考えたらしいよ」
素男「へぇー、運動すると自動的に線が引けるのか！？」
樺先輩「今のを式で表してみると、こんな風になるよ。」

無数の線を引いて面積ができることを、例えば、ｘの部分がＢからＡに向かって動いて三角形ができる場合、 と表し、ｙによる三角形の場合は、と表すとする。上の図と下の図を比較すると、上のｘ、ｙが下のｙ、ｘになっているように 必ずｘの相手方ｙに、同じ長さの線分が現れるので、 ところで、この二つで長方形ができるから  だから

聡子「三角形の面積の公式ですね。」素男「それで、四角錐の体積はどうして出したんスか？」
樺先輩「前の図でｘとｙを一辺とする二つの正方形を作り、ｘとｙを動かしていくと、無数の正方形によって二個の四角錐ができるよね。」
素男「よくわからないス」
樺先輩「それじゃ図を描いてみるか。ＰＱがＡＢからＣＤ方向へ動いて行くと左側に先端に向かう、右側には底辺に向かう角錐ができる。 ＰＱがＣＤに達したときには、同じ形の四角錐がふたつできるよ。」
 

素男「わかるス。それで体積はどうやって計算するんですか？」
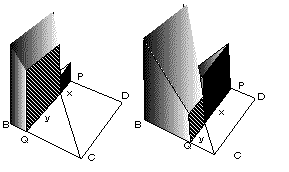
樺先輩「正方形を立ち上げる土台の平面をこんな風に、縦に二等分するＧＥという直線を引くよ。ｙの長さの中でＧＥより左にある線分をｚとするよ。ＰＱが動くときｘとｙから正方形を作っていったけれど、今度は、ｚを一辺とする正方形も作るんだ。」
 

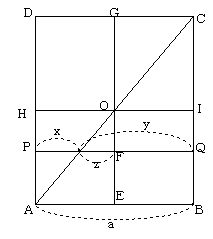素男「なんだかこんがらがってきたス」
樺先輩「そのなんとかスというのやめてくれない。ぼくは酢の物が苦手なんだ」
素男「はい、すいません。そうしまス」
樺先輩「それじゃ、また絵を描いてみるか。」
素男「ｚはＨＩ線に近づくと０になるけど、その先はどうなるんですか？」
樺先輩「今度はｘの中でＧＥより右にある部分をｚとするのさ」
素男「あっそうか」聡子「すると、ｚによっておなじ四角錐が二つ出来るんですよね」
 

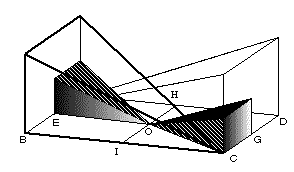樺先輩「そうだよ。それで、ｘによってできる四角錐とｚによってできる一個の四角錐の体積を比べてみると、ｚの方はｘの方の８分の１になるよね」
素男「えっ？半分じゃないの？」
聡子「正方形の一辺を半分にすると、元の正方形の４分の１になるでしょう。」
素男「ああそうだね。それで、体積になると？」聡子「直方体の一辺を半分にすると、元の体積の８分の１になるっしょ。」
樺先輩「直方体の例がでたけど、一般に相似の図形では、長さを半分にすると面積は４分の１，体積は８分の１になるよ。それで実際に計算してみるよ」

直方体の体積；∫ａ２＝ａ２ｈ、ところで、ａ＝ｘ＋ｙ　なので、 　　　∫ａ２＝∫(ｘ＋ｙ)２＝∫ｘ２＋∫ｙ２＋２∫ｘｙ＝ａ２ｈ　・・・�@、　 　　　ｘ＝1/2・ａ−ｚ、ｙ＝1/2・ａ＋ｚ、から、　ｘｙ＝1/4・ａ２−ｚ２。 ＰＱが中央線ＨＩを超えたら、　 　　　ｘ＝1/2・ａ＋ｚ、ｙ＝1/2・ａ−ｚ、から、　ｘｙ＝1/4・ａ２−ｚ２。 おなじ結果になる。 　ところで、∫ｚ２　は、ＡＥを始線として動線1/2・ａがＨＯまで行き、さらにそれを超えてＧＣまで行くときにできる立体図形の体積を表す。ＡＥからＨＯまでの図形は、求めるべき四角錐と相似で辺、高さが半分なので、体積は、８分の１になる、したがって、 　　　　∫ｚ２＝２･1/8∫ｘ２＝1/4・∫ｘ２ ゆえに、 　　　　∫ｘｙ＝∫(1/4・ａ２−ｚ２)＝1/4・∫ａ２−∫ｚ２＝1/4・ａ２ｈ−1/4・∫ｘ２ �@の式は、∫ｘ２＝∫ｙ２　を使って、２∫ｘ２＋２∫ｘｙ＝ａ２ｈ 上記の結果を使って、２∫ｘ２＋２(1/4・ａ２ｈ−1/4・∫ｘ２ )＝ａ２ｈ すなわち、3/2∫ｘ２＝1/2･ａ２ｈ 　　　　　∫ｘ２＝2/3･1/2･ａ２ｈ ＝1/3･ａ２ｈ

聡子「あっ。四角錐の体積。面積×高さ÷３だ。」
素男「あっ。ホントだ。やっと３分の１に出会った。だけど、回りくどくてなんかスットした気持ちになれないな。」
樺先輩「そうだけど、一般に理屈を追うと、本当に納得するまで時間がかかるよ。」
素男「先輩！四角錐は分かったんですが、円錐の場合はどうするんですか？」
聡子「さっきやったしょ！カヴァリエーリの法則だって！」
素男「おおそうだった。だけど、その法則はどうして出すんですか？」
樺先輩「書いて説明するよ」

例えば、さっきの三角形の面積から話を進めるよ。 動線分のｘを３倍して動かして作る三角形と元の三角形の面積を比較するよ。 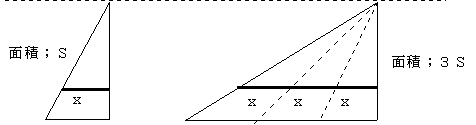　　　　　 ｘを総計すると∫ｘ＝Ｓ、３ｘを総計すると、∫３ｘ＝３Ｓ だから、　 ∫３ｘ＝３∫ｘ 　もう一つ、動面積を４倍にした四角錐の場合をみるよ。 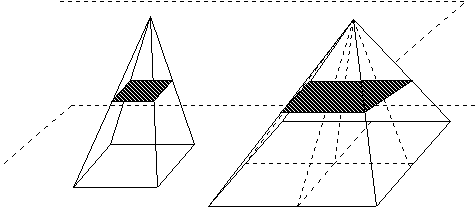　　　 　　　 動平面ｘ２を総計して、∫ｘ２＝Ｖ　ｘ２の４倍をを総計すると、 　　　　　∫４ｘ２＝４Ｖ　つまり、∫４ｘ２＝４∫ｘ２ 　一般に、∫ｋｘ＝ｋ∫ｘ 平行線の範囲内の全ての位置で、動線分がｋ倍ならば面積もｋ倍になる。また、 　　　　　∫ｋｘ２＝ｋ∫ｘ２ 平行平面の範囲内の全ての位置で断面積がｋ倍であれば、体積もｋ倍になる。これが「カヴァリエーリの定理」だ。

素男「それにしても先輩、ずいぶんカヴァリなんとか先生の説に詳しいですね。ひょっとして、樺先輩の御祖先ですか」
樺先輩「カヴァリエーリは１７世紀のイタリア人。今高校で習っている数学の渡邊先生から、カヴァリエーリのこと宿題に出されたんだ。それで、一寸前にレポートを書き終わって中学校にやってきたわけ。」
聡子「ああ、そんなんだ。さっきから樺先輩のこと尊敬しまくっていたんですよ」
素男「ところで、高校にはこんな変な宿題を出す先生もいるんですね」
聡子「そんなことより、線が動いて面をつくる。面が動いて体積を作るってすごく素敵なアイディアみたい。」
素男「それがさぁ。ちょっと変だよ。線が動いて面を作ると言うけれど線には幅がないだろう。幅がないのに面がでいるわけないよな。それに、面には厚さがないだろう。厚さが０の物がいくら沢山集まっても体積になるわけないよ！」
聡子「だけど、実際に今やったようにちゃんと体積が求まったでしょ。」
素男「それもそうだけど。どうも腑に落ちないな。先輩どうなんですか？」
樺先輩「今素男君が言ったこと。当時もずいぶん批判されたんだ。けれど、カヴァリエーリはキチンとした答を出せなかったんだ。どうやら線や面の運動に何かをつくり出す秘密があると考えたんじゃないかな」