エントロピー最大の確率密度関数は、正規分布関数である。
はじめに
小針日見宏著「確率・統計入門」1973岩波書店
「正規分布のことを、別名ガウス分布とも呼ぶが、ガウスは測量の仕事を長年やっている間に、球面幾何学と誤差の分布についての理論を作り上げたと伝えられている。整数論を本来の志としていた代数学者がガウスがこれである。大いに見習いたいものではないか。」(p.117)
かねてから、ガウスがどうしてあの正規分布の確率密度関数をみつけたのか興味を持っていた。
二項分布から導くのが一般的である。ただし、高等学校の指導要領にはこの導出はない。
教える側としては、一応マスターしておかなければならない事項だが、これとは別に、エントロピーを最大にする分布が正規分布であることが知られている。
かつて、私が卒業論文で情報理論を取り上げたが、その折に触れた事項でもある。今から四十年も昔のことで、いわゆる「60年安保」時代のことであった。今この卒論を読み返してみて、冷や汗がでるほど、論証が雑で、科学の論文らしくない、曖昧な用語が無造作に使われ、自分の未熟さを痛いほど知らされた。
この度は、再び、情報量から正規分布を導く過程だけをとりだして、復習してみた。以下はその概要である。何らかの参考にしてもらえれば幸いである。
情報量 参考文献;河田竜夫、国沢清典『現代統計学』下巻第15章p.p.163~185
ある情報(information)の“情報量”というものを考えよう。
「犬が人に噛付いた」という情報と「人が犬に噛付いた」という情報では、後者の方がニュースヴァリューが大きい。従って、その“情報量”も大きいと見る。
ある殺人事件の犯人が「男である」との情報とシャイロックホームズが言ったように「背が高く左利きの男で右足が跛で厚底の猟靴をはき、灰色の外套を着て、パイプを使ってインド産の葉巻を吸う奴でポケットにはよく切れないペンナイフをいれていたりする」という情報では、後者の方が“情報量”がはるかに大きい。
顕微鏡下の物体が、「植物である」という情報と、「桜の花の花粉である」との情報では、後者が“情報量”が大きいことは一見して解る。
従って、“情報量”を数量的に規定するには、その情報の基になる事象の出現確率で表現すればよいことがわかる。即ち、
珍しい事⇔出現確率が小さい⇔“情報量”が大きい。
ありふれたこと⇔出現確率が大きい⇔“情報量”が小さい
という図式が成り立つ。
もちろん“事象の情報量”と“事象の意義”とは別である。どこかのイワン・ペトロヴィッチ・某が死んだという事象とヨスィフ・ヴィサリオノビッチ・スターリンが死んだという事象では、死ぬ確率が数学的に同じでも、意義が非常に違う。そのような意義をここでは捨象してしまう。
出現確率が小さい事象すなわち珍しい事象がおこるかどうかは、不確実なものである。そんな事がおこるかどうか分からない事が起これば、それは、珍事でありそれだけその事象の情報量も大きいとみなす。即ち“不確実さ”と“情報量”は表裏の関係にある。従って、その量的表現がおなじであることになんら不合理はない。
数学的規定
1.前提
(ⅰ) 事象Eの出現確率P(E)=p、事象Eが出現したと言う情報の情報量を
I(E)とするとき、I(E)=I(p);情報量Iは確率pの関数である。
(ⅱ) I(p)≧0、p=1⇔I(p)=0;その値を非負にしておく。
(ⅲ) I(p)は、pの連続関数で、1/pにつき単調増大;稀なものほど値が大きい。
(ⅳ) I(1/2)=1;値の基準を定める。
(ⅴ) ![]() 、
、![]()
2. 関数形の決定
P(Ei)=p (i=1,2、…n) と仮定する。
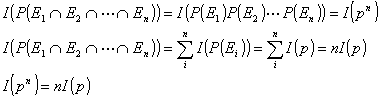
同様に
![]()
与えられたp、q、nに対して、適当なmをとって、次の式を作ることができる。
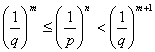 …①
…①
上記各辺を確率に持つ事象の情報量は、次のようになる。
I(qm)≦I(pn)<I(qm+1)
mI(q)≦nI(p)<(m+1)I(q)
各辺をnI(q)で割って、
![]() …②
…②
①式各辺の自然対数をとると、
![]()
![]()
![]()
各辺をn・logqで割って、logq<0
![]() …③
…③
|
│← ε →│
↑ ↑ ↑ ↑ a x、 y a+ε │x-y│<ε |
②と③より、上図定理を参照して
![]()
n→∞ のとき、
![]()
![]()
前提ⅳより、
I(1/2)=1、klog1/2=1
対数の底を2とすると、 k(-1)=1、ゆえに、k=-1
I(p)=-log2p
例(1) 64室あるアパートに住んでいる人の部屋の位置を知っているのは、単にそのアパートに住んでいることを知っているよりは、どのくらい多く情報量を持っているか。
(解) そのアパートが64室あるとすると、ある部屋に住んでいる確率は1/64、従ってその情報量は、 I=─log2(1/64)=6
例(2) 有権者の40%が自民党支持で、自民党支持の35%は男性であるとする。「日本太郎は自民党支持者である」という情報の情報量はいくらか?
(解) ある人が自民党支持である確率;p1=0.4
自民党支持者中の男性である確率;p2=0.35
その人が男性である確率;p3=0.5
その人が男性であり、自民党支持者である確率;p4
男性が自民党支持者である確率;px
p4=p1・p2=p3・px
![]()
![]()
=log20.5─log20.4─log20.35≒─1+1.3219+1.5145=1.8364
エントロピーentropy 参考文献;A.I.Khinchin Mathematical Foundation of Information Theory Dover Publications,inc,N.Y.1957
起こりうる事象A1、A2,…Anが互いに排反で、それぞれの確率p1、p2、…pnが分かっている時、つぎのような表式でそれを表す。これを有限表式(finite scheme)という。
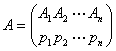
各事象がそれぞれ前述の情報量を持っていれば、有限表式全体としての情報量を考えてみることができる。その際、情報量の平均値(期待値)をとる。
H=─Σpilogpi
これをエントロピーと名づける。
次のような有限表式を持つ完全系を考える。(ある試行の結果として、必ず起こる事象の集合を完全系という)
![]()
![]()
どちらの系が不確実性(曖昧さ)が大きいかというと、どちらが出るか予断が許せない状態を持つ後者である。ちなみにそれぞれのエントロピーを計算すると、
H(A)=─0.99・log20.99─0.01・log20.01=0.01435+0.06643=0.08078
H(B)=─0.5・log20.5─0.5・log20.5=0.5+0.5=1
元来エントロピーは物理学用語で、熱学第二法則=不可逆の量的表現の測度として表れる。つまり、無秩序性の量的表現である。
よく考えてみると、状態が無秩序であるとの現象として“不確実性(曖昧さ)”と“情報”が紙の裏表の如くに表れる。だから、無秩序性が本質的なもので、その現象としての“不確実性(曖昧さ)”と“情報”が表れる。従って、両者の量的表現が一致していても何ら不思議はなく、むしろ当然のことである。エントロピーの概念は無秩序性の測度であり、「不確実性(曖昧さ)」「情報」の量的表現でもある。
例(3)
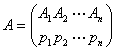 において、H(A)を最大ならしめる、確率p1、p2、…pnは何か?
において、H(A)を最大ならしめる、確率p1、p2、…pnは何か?
(解) Σpi=1の条件下で、 H(A)=─Σpilogpiを極大にするp1、p2、…pnを求める。
ラグランジュ(Lagrange)の乗数法を用いて、
U=H(A)+λ(Σpi─1)
![]()
─logpi─1+λ=0
logpi=λ─1
![]() …①
…①
これをΣpi=1へ代入すると、
![]()
![]()
![]()
λ─1=─logn
これを①に戻して、
![]()
出現確率が等確率のときである。
確率変数が連続変数のときのエントロピー
離散的変数からの類推を用いて、次のように定義する。
![]()
ただし、p(x)は、確率密度関数である。
例(4) 正規分布N(μ、σ)のエントロピーを計算せよ。
(解)
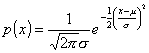
![]()
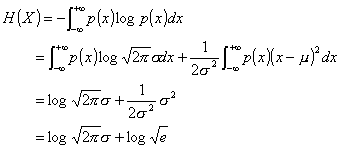
![]()
正規分布のエントロピーはσに依存する。
例(5) 平均値がmで、標準偏差σが一定のとき、最大のエントロピーを持つ、確率分布は何か?
(解)
![]()
の条件下で
![]()
を最大ならしめるxの関数p(x)を求めることである。
ラグランジュの未定係数法と類似の方法を用いて次のように変分法を使う。
未定係数をλ、μとして、次の式を立てる。
![]()
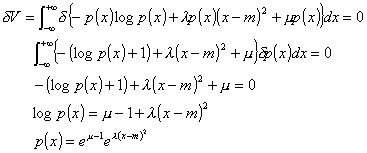
両辺を積分して
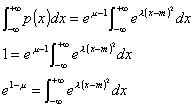
右辺について、
![]() とおく
とおく
![]()
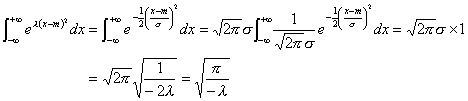
元に戻って、
![]()
これをp(x)の式に代入して
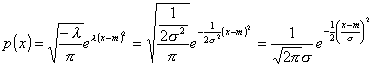
これは、N(m、σ)である。
参考文献;スミルノフ『高等数学教程』8Ⅳ巻第一分冊、p.p.189~、共立出版、1958
|
|