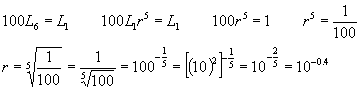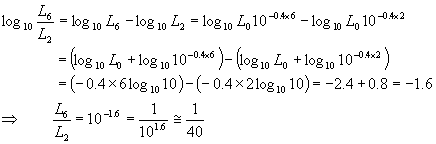対数はどのように使われているか？

　　「常用対数」の定義；底が１０の対数　ａ＝log１０Ａ　
例(１)　地震の規模　magnitude［ﾏｸﾞﾆﾁｭｰﾄﾞ］Ｍで表す。　
①　地震のエネルギーとＭとの関係式　　Ｅ；地震波のエネルギー、単位はerg＝10－７Ｊ（10７erg＝Ｊ）
                         l og１０Ｅ＝11.8＋1.5Ｍ

例(1) 兵庫県南部地震；95年１月17日；死者6308＋2、負傷者43177人　　
        Ｍ＝7.2　深度ｈ＝18km　であった。　　
       エネルギーＥ１を求めよう。　　
(解)　log１０Ｅ１＝11.8＋1.5×7.2＝22.6　　　　 　
                Ｅ１＝1022.6erg＝1015.6Ｊ≒1016Ｊ＝１京Ｊ　
練習(1) 北海道南西沖地震93年７月12日　死者202＋28、負傷者321人　　
           Ｍ＝7.8　深度ｈ＝34km　であった。　　
           エネルギーＥ２を求めよう。　　　
例(2)　Ｅ１とＥ２を比較してみよう。　　　
(解)　
    ゆえに　　　　 　　　　
練習(2) 　予想される東海沖地震では、Ｍ＝８　である。
             (1)　エネルギーＥ３ を求めてみよう。　　　
             (2)　　　　を求めてみよう。　　　　　　
             (3)　　を求めてみよう。　
                                                                     組　　出席番号　　氏名

　②　気象庁のマグニチュード（この他にいろいろな決め方がある）
       (1) 深度ｈ≦60km　のとき　　　
           ａ）　Ｍ＝log１０Ａ＋1.73log１０Δ－0.83　　　　　　　
                Ａ；中周期変位型地震計で、　　　　　　　　　
                    ５サイクル以下の波の最大地動片振幅μm　　　　　　　　　
                    東西方向の変位ｘ、南北方向の変位ｙ、　　　　　　　
               Δ；観測地から震央までの距離　km　　　
          ｂ）　Ｍ＝log１０ＡＺ＋1.64log１０Δ＋α　　　　　　　
                ＡＺ；短周期速度型地震計で、　　　　　　
                     上下動の最大地動速度振幅　10－３cm/s　　　　　　　
                 Δ；観測地から震央までの距離　km　　　　　　　
                 α；その地震計の特性補正項
        (2) 深度ｈ＞60km　のとき　　　
           c)　　Ｍ＝log１０Ａ＋Ｋ(Δ､ｈ)　　　　　　
                  Δ；観測地から震央までの距離　km　　　　　　
                   ｈ；深度　km　　　　　　
                   Ｋ(Δ,ｈ)；Δとｈの二変数関数：表になっている。　　
　例(2)　溶液１㍑の中のＨ＋の数　（Ｈ＋は活性水素）　　
          ①　6.02×10２３個＝１mol　　という。（12個＝１dz［ﾀﾞｰｽ］と同じ発想）　
      例(1)　6.02×10１５個のＨ＋ の個数をmolで表そう。　　　
               6.02×10１５個＝6.02×10２３－８個＝6.02×10２３×10－８個＝１mol×10－８　　　
              モル数を［Ｈ＋］と表せば、　［Ｈ＋］＝10－８　
      練習(1)　次のＨ＋ の個数をmolで表してみよう。　モル数も表してみよう。
            (1)　　6.02×10１６個＝　　　 ［Ｈ＋］＝　
            (2)　　6.02×10１７個＝　　　 ［Ｈ＋］＝　　
         ②　溶液１㍑の中のＨ＋のモル数を［Ｈ＋］で表し、　　　　　　
               ｐＨ＝－log１０［Ｈ＋］　　を定義する。（ｐＨはドイツ語読みで[ペーハー]）　
      例(2)　モル数［Ｈ＋］をｐＨで表してみる。　　
                       　[Ｈ＋］＝10－８　のとき　ｐＨ＝－log１０［Ｈ＋］＝－log１０10－８＝８　
     練習(2)　次の［Ｈ＋］をｐＨで表してみよう。
            (1)　［Ｈ＋］＝10－７　のとき　　　　　　ｐＨ＝　　
            (2)　［Ｈ＋］＝10－６　のとき　　　　　　ｐＨ＝　　　
                                                                                       組　　出席番号　　氏名

例(3)　星の光度等級　magnitude　［ﾏｸﾞﾆﾁｭｰﾄﾞ］
        ①　紀元前１５０年頃、ギリシャの天文学者ヒッパルコス　Hipparchos　は、　　
             星の明るさを１～６等星までに分けた。
        ②　1830年頃、イギリスのハーシェル　J．Herschell（天王星を発見した人の息子）　　
             次の関係「明るさは等級に応じて一定の割合で減少する」を明らかにした。　　
             [1]　等級　　１→＋１→２→＋１→３→＋１→４→＋１→５→＋１→６　　　　
                   明るさ　L１ →×ｒ→L２→×ｒ→L３→×ｒ→L４→×ｒ→L５→×ｒ→L６　　　　　　　　但し　０＜ｒ＜１　　　
             [2]　L１＝100L６
        ③　1850年頃、ポグソン　Ｎ．Pogson　は次の式を明らかにした。　　
              等級　　１　　２　　　　 ３　　 　　４　　　　　５　　　　　６　　
              明るさ　L１ 　　L２＝L１ｒ　　L３＝L２ｒ　　L４＝L３ｒ　　L５＝L３ｒ　　L６＝L３ｒ　　　　　　　　　　
                                         　　　　　 ＝L１ｒ２　　 ＝L１ｒ３　　 　 ＝L１ｒ４　　　＝L１ｒ５
               　　 　　　
      　④　０等星を基準にすると、１等星の明るさは；　L１＝L０ｒ、２等星のは；L２＝L０ｒ２　以下同様、ｍ等星では、

     　例(1)　光害が無いところでは、人間の目は６等星までみえる。都会では、２等星しか　　　
                見えない所が多い。６等星と２等星の明るさを比較してみよう。
　　　　
 　　
  練習問題；すばる（８.２ｍ望遠鏡ハワイ・マウナケア）は、２７等級まで見える。　　　　　
                 ２７等級の明るさと６等級の明るさとを比較してみよう。　　　

                                                                                                              組　　出席番号　　氏名
　マサルのレポートに戻る
　ホームページに戻る