���̋����𑪂�
�]���藝�|���ʁE����
�n粏��i�D�y�Վ��H�ƍ��Z�j
������
��R�V��S�����w���猤�����
�P�X�X�V�N�V���Q�W���A�Q�X��
�D�y�s�t���w�Z
|
|
�T�@�͂��߂�
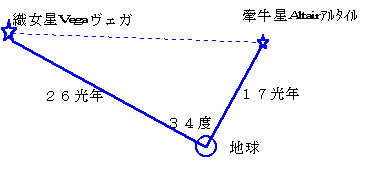
���G�n�����猡�����܂ł́A�P�V���N�A�������D�����܂ł́A�Q�U���N�A��̐���]�ފp�x�́A�R�S�x�ł���B�������ƐD�����̊Ԃ̋��������߂�B
���G
�@�@�@�@�@�@�`�u�Q���u�d�Q�{�d�`�Q�|�Q�u�d��d�`cos34��
�@�@�@�@�@�@�@�@�@�@�@�@�@�@���Q�U�Q�{�P�V�Q�|�Q�E�Q�U�E�P�V�E�O�D�W�Q�X�O
�@�@�@�@�@�@�@�@�@�@�@�@�@�@���Q�R�Q�D�Q
�@�@�@�@�@�@�@�`�u���P�T�D�Q�S
���̖��́A���ȏ��i�O�ȓ��j�ɂ��f�ڂ���Ă���D�ꂽ���ł��B�ЂƂ́A���ʂ̗̈��n�ォ��V�E�֔�Ă��邱�ƁA�����E�D���̗����ꂪ���n�ɂ����āA���}�����������Ă邱�ƁB��N�Ɉ�x�̈�������������Ȃ��u��l�v�̋��������߂邱�Ƃ��A�D��S���������ĂĂ���̂ł��B
�U�D�n���P���Ԃ̋���
�P�D�N���������g����
�Ƃ���ŁA�n������P���܂ł̋����͂ǂ̂悤�ɑ��肷��̂ł��傤���H�@
�ړI�̓V�̂��`�Ƃ��A�n�������z�r�̎�������]���Ă���~�i�ȉ~�j�̒��a�̗��[���d�P�A�d�Q�@�Ƃ���Ƃ��A�ϑ��n�Ǝ��������܂��Ƃ邱�Ƃɂ���āA�����̒��p�O�p�`���ł��܂��B
�@�@�@�@�@�@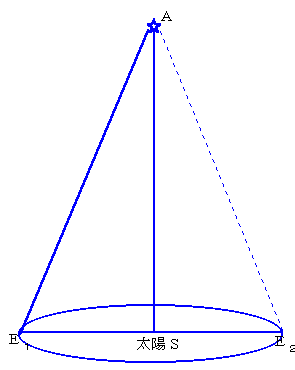
�ڂd�P�`�r�@��N�������ƌ����܂��B���ꂪ�A����ł���A���`�d�P�r�@�ɂ��āA
�d�P�r���P�D�S�X�T�X�V�W�V�O�~�P�O�P�P���i�P�V���P�ʁ��`�t�j�����m�Ȃ̂ŁA�ӂ`�d�P�����߂邱�Ƃ��ł��܂��B
�@
��F�@�P���^�E���������̔N�������́@�O�D�V�T�b�ł��B���̐��܂ł̋����͂����炩�H
���F�@���̐����`�A�n�����d�A���z���r�Ƃ��āA�O�p�`�`�d�r�́A�ڂr�����p�A
�@�@�@�@�@�`�d�Esin�ڂ`���d�r
�@�@�@�@�@![]() �@�@
�@�@
�ڂ`�͔����Ȃ̂ŁA���W�A���ő���Asin�ڂ`���ڂ`
�@�d�r���P�`�t���P�D�T�O�~�P�O�W����
�ڂ`���O�D�V�T�O�����O�D�V�T�O�~�S�D�W�T�~�P�O�\�U�@���R�D�U�S�~�P�O�|�U
�`�d���d�r���ڂ`���S�D�P�Q�~�P�O�P�R����
�@�@���S�D�P�Q�~�P�O�P�R�������X�D�S�U�~�P�O�P�Q�����^���N���S�D�R�U���N
�Q�D�N���������o�̋�J
�R�y���j�N�X���n��������āi�P�T�S�R�N�j�ȗ��A�N�����������肳���ł��낤�Ƃ̌����݂ŁA�����̓V���w�҂����܂��܂ȋ�J�ƍH�v�����Ȃ��瑪��ɏ]�����܂����B
�P�U�V�T�N���������߂đ��肵���n�D�b�D���[�}�[���A���̖��ɂ����߂Ď��g�݂܂��������o�o���܂���ł����B
���̌�A�F���������Y�̔����������āi�P�V�R�R�N�A�b�D�l�D�z�[���A
�P�V�T�T�N�A�i�D�h�����h�j�A���ܖ]���������B���A�P�W�R�W�N�ɂe�D�v�D�x�b�Z�����A�w���I���[�^�[�Ƃ������w��B���g���āA�������̂U�P�Ԑ��̔N�������𑪒肵�܂����B
���̊p�x�́A�O�D�Q�X�S�b�ł��B���͂P�D�O�̐l����������̂́A�P�����U�O�b�Ƃ����Ă��܂��B�����ɔ��������킩�肢��������Ǝv���܂��B���Ȃ݂ɁA���⑾�z�̎����a���R�O�����P�W�O�O�b�ł��B
���݂́A�ʐ^�B�e�̃t�B�����̔�r���炱�̊p�x�𑪒肵�܂��B�������A�������́A�덷�̌��E���ɓ����Ă��܂����肪�s�\�ɂȂ�܂��B
�܂��A���_�܂ł̋����𑪒肷����j�́A��̃h���}���ς�v�����������܂��B
���̂�����́A�g�c�����Y���u�]�������B�j�v�㊪�i�P�X�X�S�C�������V���Ёj�A
�W�����E�O���r������{�z��|��u�r�b�O�o���̒T���|�F���͂ǂ��������Ă������v�i�P�X�W�W�N�A���e�B�[�r�[�G�X�E�u���^�j�J�j���Q�Ƃ��܂����B
�V�D�P���Ԃ̎��������߂��B
�P�D�ʒu�V���w�����ʓV���w�̂���
�Ƃ���ŁA��]�ދ������R�S�x�́A�ǂ̂悤�ɂ��đ��肵���̂ł��傤���H�g�����V�b�g���g���Ē��ڑ��肷�邱�Ƃ��ł��܂����A�P���́u�Ԍo�A�Ԉ܁v�Ƃ����Ă�����W�����Ƃ߂��Ă��܂��̂ŁA�������Ɍv�Z�ŋ��߂邱�Ƃ��ł��܂��B
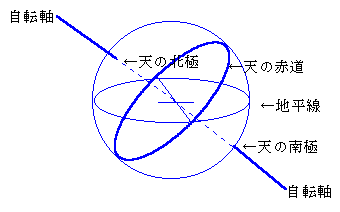
�n���̎��]�̂��߂ɁA�n����Ă���V�����A�����琼�Ɍ������Ă������Ɖ�]���Ă��܂��B�]���āA�V����̐��́A�����琼�։�]���Ă���悤�Ɍ����܂��B������u�����^���v�ƌ����܂��B�����^���ɂ���Ăł���ő�̉~���u�V�̐ԓ��v�ƌ����܂��B
�@�@
�V����̓V�̂́A�V�̐ԓ��ɕ��s�ɓ����^�������Ă��܂��B�V�͈̂�N���ԓ��ɑ��Ĉʒu��ς��܂���B�������A���z�́A�N�Ԃ�ʂ��āA�ԓ��ɑ��Ĉʒu��ς��Ă����܂��B���̂悤�ɔN�Ԃ�ʂ��āA�V����̑��z�̒ʂ铹���u�����v�i�����ǂ��j�ƌ����܂��B�������ԓ��ƌ����_���t���_�ƏH���_�ł��B
�@�����^���̎����V���ƌ����_���u�V�̖k�Ɂv�u�V�̓�Ɂv�ƌĂ�܂��B
�V�̗��ɂ�ʂ��~���q�ߐ��ƌ����܂��B�t���_��ʂ�q�ߐ���{���q�ߐ��ƌ����܂��B�{���q�ߐ����瓌�Ɍ������āA�p�x��t���܂��B������u�Ԍo�v�ƌĂт܂��B���ʂ͘Z�\���@�ɂ�炸�A���Ԗ@�ŕ\�����܂��B�P�W�O�x�ƌ��킸�P�Q���ƌ����A�P�T�x���킸�P���Ԃƌ����܂��B
����V�̐ԓ����痼�ɂɌ����āA�p�x��t���܂��B������u�Ԉ܁v�ƌ����܂��B�k�ɂւ̓v���X�̊p�x���A��ɂɂ̓}�C�i�X�̊p�x���g���܂��B
�@�V����̓V�̂́A�Ԍo�ƐԈ܂ł��̈ʒu��\�����Ƃ��ł��܂��B
�@�@�@�@�@�@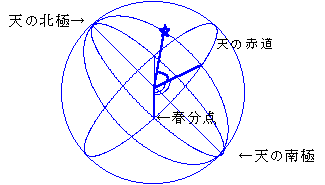
�Q�D���ʎO�p�`
�V����̎O�_�ɂ���āA���ʎO�p�`��`�����Ƃ��ł��܂��B
���̔��a���P�Ƃ��āA���ʏ�̕ӂ́A�p�x�ŕ\���܂��B���p�́A���}�̂悤�ɒ�`���܂��B�@�@�@�@�@�@�@�@
�@�@�@�@�@�@�@�@�@�@�@�@�@�@
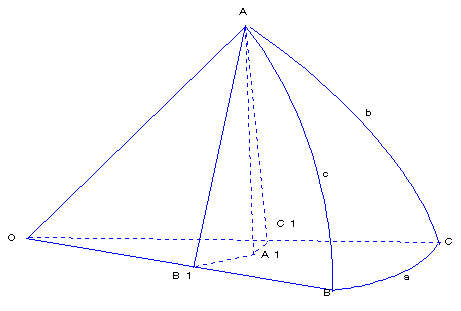
�@�����ڂa�n�b�@�@�@�@�@�����ڂb�n�`�@�@�@�@�����ڂ`�n�a�@
�ڂ`���ڂa�P�`�b�P�@�@�@�@�ڂa���ڂ`�a�P�`�P�@�@�@�ڂb���ڂ`�b�P�`�P
�i�ڂn�a�P�`���ڂn�b�P�`���ڂq�j�@�@�i�ڂn�a�P�`���ڂn�a�P�`�P���ڂq�j�@�i�ڂn�b�P�`�P���ڂn�b�P�`���ڂq�j
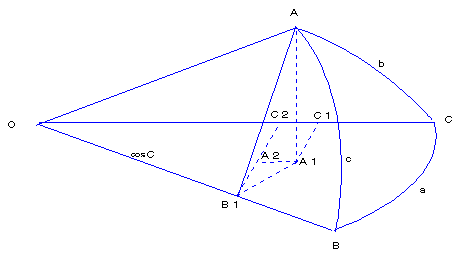
�R�D���ʎO�p�`�̗]���藝
�@���ʎO�p�`�ɉ����Ă��A�u�]���藝�v�ƌĂ��藝������܂��B
�@
�@�@
�@�@
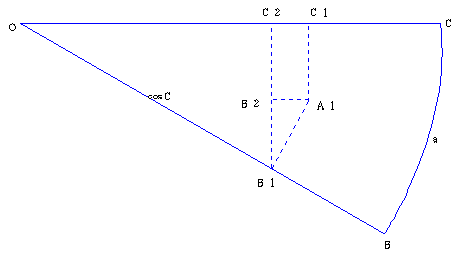
�@�`�a�P��sin��
�`�P�a�P���`�a�P�Ecos�a��sin���Ecos�a
�n�b�P��cos���A�n�b�Q��cos���Ecos���@
�`�P�a�P��sin���Ecos�a�@�@�@
�`�Q�`�P���`�P�a�P�Esin����(sin���Ecos�a)sin����sin��sin��cos�a
�@�n�b�P���n�b�Q�{�b�Q�b�P
�@�@�@�@���n�b�Q�{�`�Q�`�P
�@cos����cos��cos���{sin��sin��cos�a�@�i�]���藝�j
�@�֊ϊ��ɂ���āA
�@cos����cos��cos���{sin��sin��cos�b
�@cos����cos��cos���{sin��sin��cos�`
�@
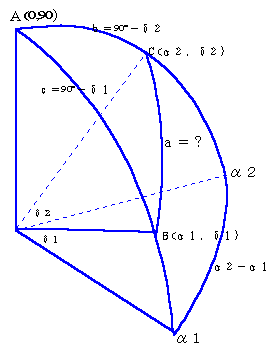
�S�D�Ԃ̎��p�i�������j�����߂��������
�@�V�̂̍��W���i�Ԍo�A�Ԉ܁j�̂悤�ɕ\�킵�A�V�̖k�ɂ��`�A�V�̂��a�C�b���āA
�a(���P�C���P)�A�b(���Q�C��2)�Ƃ���ƁA���}�̂悤�ɂȂ�܂��B
�@�@ �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
�@�@�@�@���߂鎋�p�i�������j�����Ƃ��āA�]���藝��K�p�����
�@cos����cos��cos���{sin��sin��cos�`
�@��cos(90���|���Q)cos(90���|���P)�{sin(90���|���Q)sin(90���|��)cos(��2�|���P)
�@�@��sin���Qsin���P�{cos���Qcos���Pcos(��2�|���P)
�@��sin���Psin���Q�{cos���Pcos���Qcos(��2�|���P)
��G�D�����i�P�W���R�U�D�X���A�R�W���S�V���j�A
�������i�P�X���T�O�D�W���A�W���T�Q���j�ł��B
�Ԃ̎��p�i�������j�����߂Ă݂悤�B
���F
�@�������p�x�Ɋ��Z���܂��B
�@�@�P�W���R�U�D�X�����P�W���{(�R�U�D�X���U�O)�����P�W���{�O�D�U�T�P��
�@���P�W.�U�T�P�����P�W.�U�T�P���~�P�T���^�����Q�V�X���Q
�@�@�P�X���T�O�D�W�����P�X���{(�T�O�D�W���U�O)�����P�X���{�O�D�W�S�V��
�@���P�X�D�W�S�V�����P�X�D�W�S�V���~�P�T���^�����Q�X�V���V
�@����x�Ɋ��Z���܂��B
�@�@�R�W���S�V�����R�W���{(�S�V���U�O�j�����R�W���V�W
�@�@�@�W���T�Q�����@�W���{(�T�Q���U�O�j�����@�W���W�V
�@�D�����i�Q�V�X���Q�A�R�W���V�W�j�A�������i�Q�X�V���V�A�W���W�V�j
�@�@���߂鎋�p�����Ƃ��āA�]���藝��K������ƁA
cos����sin���Psin���Q�{cos���Pcos���Qcos(��2�|���P)
�@�@��sin�R�W���V�Wsin�W���W�V
�@�@�@�@�@�{cos�R�W���V�Wcos�W���W�Vcos(�Q�X�V���V�|�Q�V�X���Q)
�@�@���O�D�O�X�U�U�{�O�D�V�R�O�S���O�D�W�Q�V�O
����cos�|�P�O�D�W�Q�V�O���R�S���Q�P
�W�D��葢��̂��߂̎���
�P�D�Ă̑�O�p�`
�@�Ս����F�KVega�i�D�����j�A�h���A���^�C��Altair�i�������j�A
�������f�l�uDeneb
�@�ʒu�́@�@�@�@Vega�i�P�W���R�U�D�X���A�R�W���S�V���j�@�@�Q�T���N
�@�@�@�@�@�@�@�@Altair�i�P�X���T�O�D�W���A�O�W���T�Q���j�@�@�P�U���N
�@�@�@�@�@�@�@�@Deneb�i�Q�O���S�P�D�S���A�S�T���P�V���j�P�W�O�O���N
�@�x�Ɋ��Z���ā@Vega�i�Q�V�X���Q�Q�T�A�R�W���V�W�R�j�@�@�Q�T���N
�@�@�@�@�@�@�@�@Altair�i�Q�X�V���V�O�O�A�O�W���W�U�V�j�@�@�P�U���N
�@�@�@�@�@�@�@�@Deneb�i�R�P�O���R�T�O�A�S�T���Q�W�R�j�P�W�O�O���N
�@���p�́A�@�@�@�ڂu�|�`���R�S���Q�O�Q
�@�@�@�@�@�@�@�@�ڂ`�|�c���R�W���O�P�T
�@�@�@�@�@�@�@�@�ڂc�|�u���Q�R���W�S�X
������̖��O�̓��e����p���܂��B�ǂݕ��́u���[�}���ǂ݁v�ł��B�]���āA�p��̔����Ƃ́A�Ⴂ�܂��̂ł����Ӊ������B
�Q�D�~�̑�O�p�`
�q�����v���L�I��Procyon�@�A�匢���V���E�XSirius�A
�I���I�����x�e���M���E�XBetelgeuse
�@�ʒu�́@�@�@�@Procyon(�O�V���R�X.�R���A�T���P�S��)�@�@�@�@�P�P�@���N
�@�@�@�@�@�@�@�@Sirius�i�O�U���S�T.�P���A�|�P�U���S�R���j�@�@�@�W.�U���N
�@�@�@�@�@�@�@�@Betelgeuse�i�O�T���T�T.�Q���A�O�V���Q�S���j�T�O�O�@���N
�@�x�Ɋ��Z���ā@Procyon(�P�P�S���W�Q�T�A�T���Q�R�R)�@�@�@�@�P�P�@���N
�@�@�@�@�@�@�@�@Sirius�i�P�O�P���Q�V�T�A�|�P�U���V�P�V�j�@�@�@�W.�U���N
�@�@�@�@�@�@�@�@Betelgeuse�i�W�W���W�O�O�A�O�V���S�O�O�j�@�T�O�O�@���N
�@���p�́@�@�@�ڂo�|�r���Q�T���V�P�T
�@�@�@�@�@�@�@�ڂr�|�a���Q�V���O�X�O
�@�@�@�@�@�@�@�ڂa�|�o���Q�T���X�T�R
|
|
�}�T���̃��|�[�g�ɖ߂��@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���������Z�T�[�N���̕�