-関数とグラフ-
1.直交座標(直角座標)と極座標
座標:平面上の一点Pの位置を定めるためには、平面上に2本の相交わる直線を引き、交点から、それぞれの直線に平行に測定して、その距離xおよびyを与える。 このxおよびyはP点の座標と呼ひ、P(x,y)と表記する。また、2本の直線を座標軸(x軸およびy軸)、交点を座標の原点という。一般には、この座標軸が直交する直交座標系(直角座標系)が用いられる。
極座標:直交座標系(直角座標系)の代わりに、極座標(r.θ)を用いることもある。rは定点(極あるいは原点)からP点までの距離(動径)、θは線分OPと定点Oを通る定直線(原線)とのなす角(偏角)である。 直交座標系(直角座標系)との間には、次の関係がある。
2.関数
関数:関数とは、ある変数に依存して決まる値あるいはその対応を表す式のこと。
いま、2つの変数xとyがあり、xに対してyの値を決定する規則(xに特定の値を代入すると、yの値が確定)が与えられている時、変数yは、xを独立変数とする関数、あるいは簡単にxの関数という。
その対応規則を明示する時は、
y=f(x)
と記述する。一般に、記号fは関数・functionの頭文字を用いる。
3.変数と定数
変数:変数とは、未知あるいは不定の数や対象を表す文字記号のこと。特別な値をとることがあらかじめ期待されている場合、未知数とも呼ばれる。
定数に対する言葉と解され、値が変化するものとみなされる。
定数:数学上の定数とは、変数に対して、値の変らない数のこと。一般に、その実体は実数または複素数となるが、必ずしもその値が具体的に特定される必要はない。
4.1次式(比例式)と1次関数
1次式(比例式):y=ax+b (a.bは定数、a≠0)
変数yが変数xの1次式で表される時、yをxの1次関数という。
この1次式は変数xに1つの値を与えた時、それに対応する変数yがどのように定まるかを具体的に示した規則とみなすことができる。
このような対応の規則を関数と呼び、yはxの関数であるともいう。そして、このxは独立変数、yは従属変数と呼ばれる。
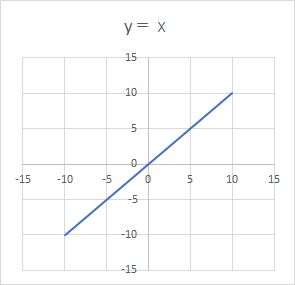
y=x
y=-x
y=3x+2
y=-2x+5
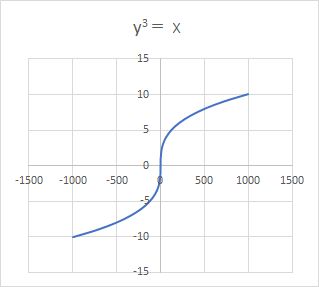
5.分数式(反比例式)と分数関数
分数式(反比例式):y=a/x(x≠0),y=a/(x-p)+q(x≠p)
分数関数とも呼ばれ、変数xの分数式で表され、グラフは原点に対称で直角双曲線となる。
一般に、ある関数のグラフ上の点Pが原点から遠ざかるに従って、1つの直線に限りなく近づく時、この直線をこのグラフの漸近線という。
y=a/x
(a>0,x≠0)
y=a/x
(a<0,x≠0)
y=a/(x-p)+q
(x≠p)
y=1/(x-2)+3 → y=(3x-5)/(x-2)
6.2次式と2次関数
2次式:y=ax2+bx+c (a.b.cは定数、a≠0)
2次式で表される関数を2次関数という。
y=ax2 (a≠0)
y=a(x-p)2 (a≠0)
y=a(x-p)2+q (a≠0)
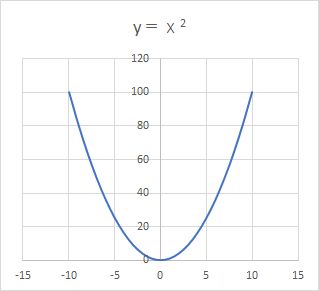
y=x2
y=2x2
y=(1/2)x2
y=-x2
y=-2x2
y=-(1/2)x2
y=(x+5)2
y=(x+5)2+6
y=(x+5)2-6
y=-(x-5)2+6
一般に、2次関数、
y=a(x-p)2+q
のグラフは、y=ax2 のグラフをx軸方向にp、y軸方向にqだけ平行移動した放物線である。
軸は直線x=p、頂点は点(p,q)、a>0の時は下に凸、a<0の時は上に凸で描かれる。
また、2次関数y=ax2+bx+cは、変形すると、
y=a{x2+(b/a)x+(b/2a)2-(b/2a)2}+c
=a(x+b/2a)2-(b2-4ac)/4a
となる。したがって、2次関数、
y=ax2+bx+c
のグラフは、y=ax2 のグラフをx軸方向に-b/2a、y軸方向に(b2-4ac)/4aだけ平行移動した放物線となる。
軸は直線x=-b/2a、頂点は点{-b/2a,(b2-4ac)/4a}である。
2次関数は、必ずy=a(x-p)2+qの形の式に変えることができ、これを2次関数の標準形という。
2次関数と2次方程式:2次関数y=ax2+bx+c(a≠0)のグラフにおいて、x軸との共有点、つまりx座標は、y=0を満たすxの値である。
すなわち、
ax2+bx+c=0 (a≠0)
この等式はxの2次方程式と呼ばれる。
xの2次関数、
y=ax2+bx+c=a(x+b/2a)2-(b2-4ac)/4a
のグラフがx軸と共有点を持つ(交差もしくは接触する)のは、
a>0でb/2a≧0 ならば、 -(b2-4ac)/4a≧0
a<0でb/2a<0 ならば、 -(b2-4ac)/4a≦0
の場合であり、ともにb2-4ac≧0の時である。この場合にx軸との共有点のx座標は、2次方程式ax2+bx+c=0の解となる。
したがって、
a(x+b/2a)2-(b2-4ac)/4a=0
a(x+b/2a)2=(b2-4ac)/4a
(x+b/2a)2=(b2-4ac)/4a2
これから、
x+b/2a=±√(b2-4ac)/2a
∴ x={-b±√(b2-4ac)}/2a
となる。これを2次方程式ax2+bx+c=0の解の公式という。
2次方程式ax2+bx+c=0は2つの解x1.x2を持ち、
もしb2-4ac>0ならば解は実数で異なり、
もしb2-4ac=0ならば解は実数で等しく、
もしb2-4ac<0ならば解は共役複素数となる。
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
以上
(2013年3月24日)