−図形と方程式−
1.点と直線
点は、直線、平面、三次元幾何学の基本的な要素である。点は、位置だけを持ち、長さ・面積・体積を持たない。点の性質は、相異なる2点を結ぶただ1本の直線を決定する。
線は点の集まりか? 点は存在するのか? 何があるかは、その何がどのように決まるかに依存する。何を知るかは、その何をどのように決めるかに依存する。
線は長さだけを持ち太さを持たない。1つの平面上において、平行でない2直線は1点で交わる(交点)。もしも3つの異なる点が1直線上にあれば、これら3つの点の内の1つは他の2つの間にあるということが可能になる。
1直線上にない空間の3点はただ1つの平面を決定する。平面座標(x,y)は、直交(直角)座標を構成し、横座標にx軸、縦座標にy軸をとる。
公式1:
座標平面上の異なる2点P1(x1,y1)とP2(x2,y2)を通る直線
|
= |
|
||||||||||||
座標平面上の異なる2点P1(x1,y1)とP2(x2,y2)の間の距離L
| L=√ | (x1−x2)+(y1−y2) |
線分P1P2を比m:nで分割する点P(x,y)の座標
| x= |
|
y= |
|
|||||||||||||
2.三角形
同一直線上にない平面上の3点を線分(辺)で結べば三角形を得る。
与えられた3点は三角形の頂点と呼ぶ。
三角形の隣り合った線分(辺)の各組は、三角形の内角を作る。
三角形の内角の和は180゜である。
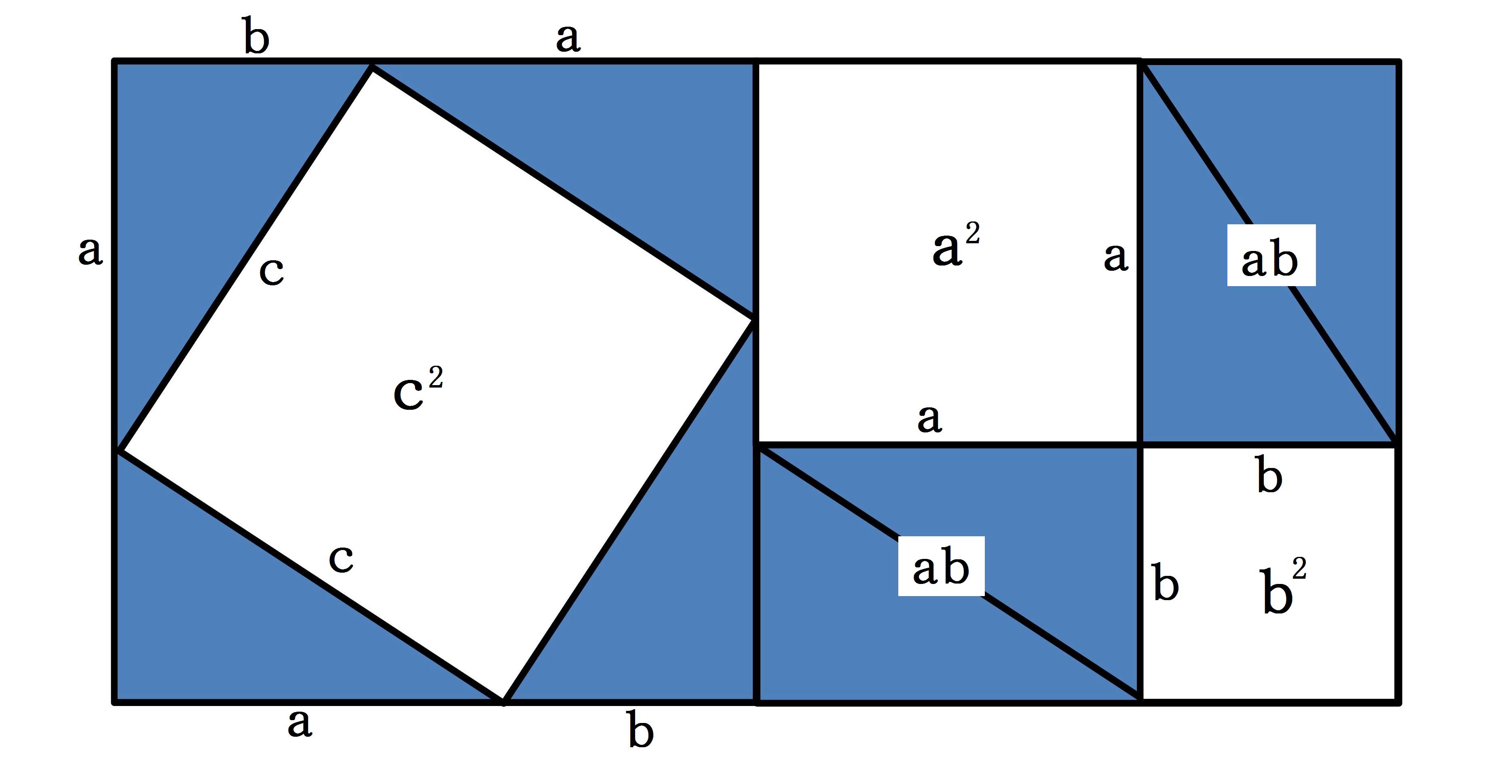
公式4:
頂点P1(x1,y1)とP2(x2,y2)とP3(x3,y3)を持つ三角形の面積Sは、
3.多角形
正多角形は、辺の長さがすべて等しく、その角の大きさも等しい。また、頂点の数が等しい正多角形は互いに相似である。 正多角形は内接円と外接円を持ち、それらは共通の中心を持っている。 もしも、正多角形の外接円の中心とn個の頂点を結べば、そこにn個の二等辺三角形が得られる。 そして、その等辺は外接円の半径に等しく、その底辺は正多角形の辺となる。
 |  |
|
| 正5角形 | 正6角形 | |
 |  |
|
| 正8角形 | 正10角形 |
 |  |
|
| 正5角形 | 正8角形 |
正多角形(正n角形)において、外接円の半径r、内接円の半径ρn、辺の長さan、および外接する正n角形の面積と周の長さとの関係を考える。
以上
(2013年3月24日)