|
-三角関数-
三角形の角の大きさと辺の長さの間の関係を研究する学問領域がある。
様々な数学の分野の中でもきわめて古くから存在し、
測量や天文学上の計算などの実用上の要求と密接に関連して生まれ、
他の幾何学的図形の各要素の量的関係や測量などへの応用を研究する。
三角法とも呼ばれている。
三角法と数表を用いれば、直接に測ることが不可能な難しい長さを、精度良く求めることができる。
三角関数は、歴史的に三角法から派生して生まれ、その呼び名は三角法に由来する。
それは、角の大きさと線分の長さの関係を記述する関数の族であり、それらを拡張して得られる関数の総称である。
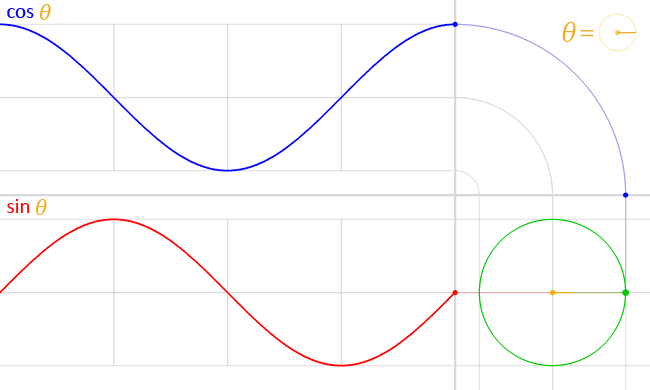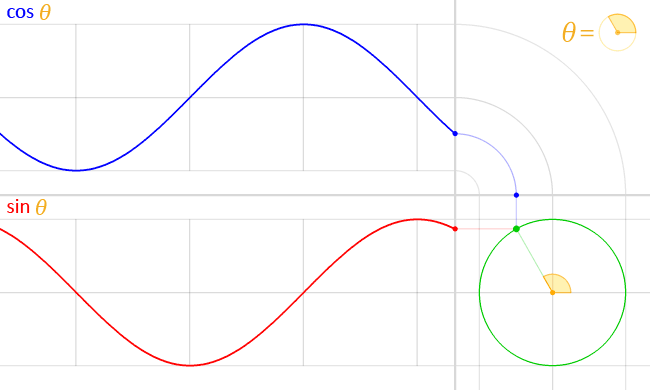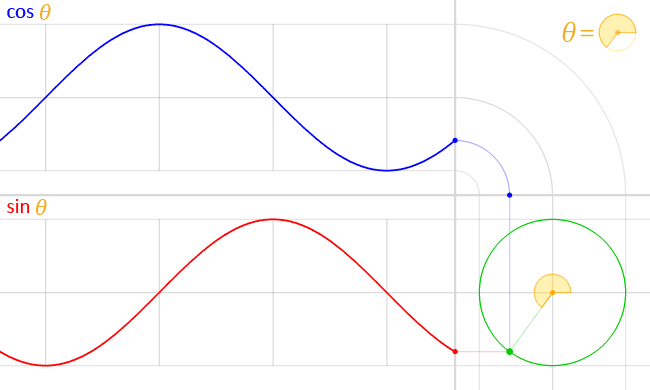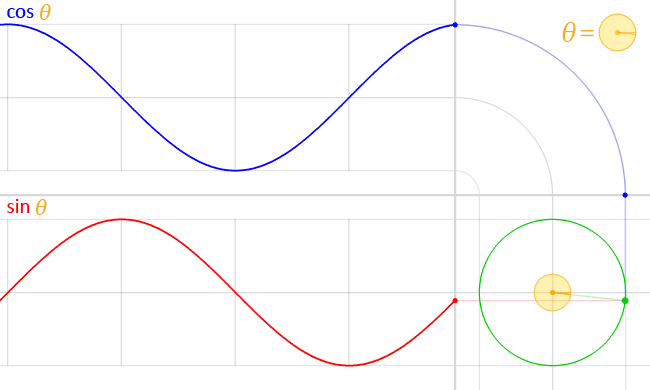
単位円を用いて定義することもでき、円関数と呼ばれることもある。
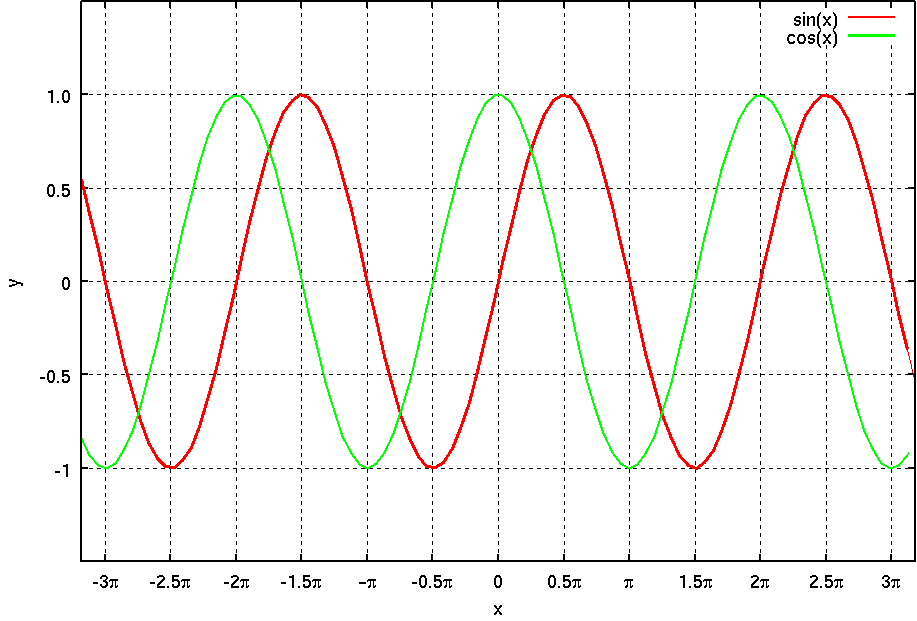
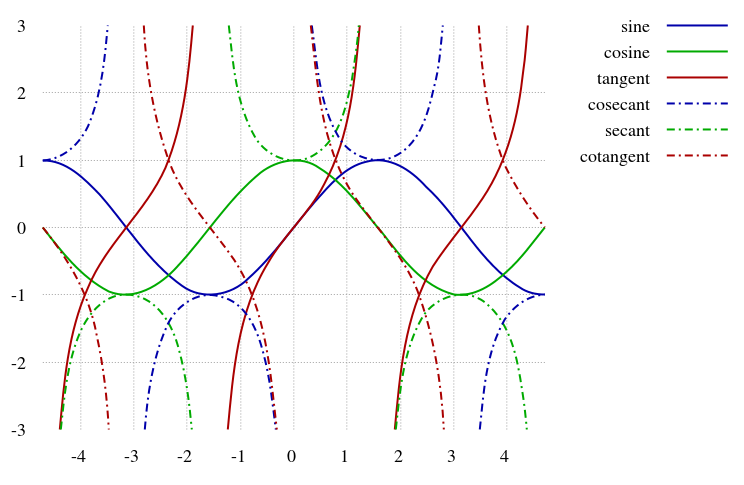
三角関数には、正弦(sin)、余弦(cos)、正接(tan)、余接(cot)、正割(sec)、余割(csc)の6つがある。これらは、原点Oに対し、原線OAと動径OPとの間の角θとすると、点PからOAに垂線PMを下せば、
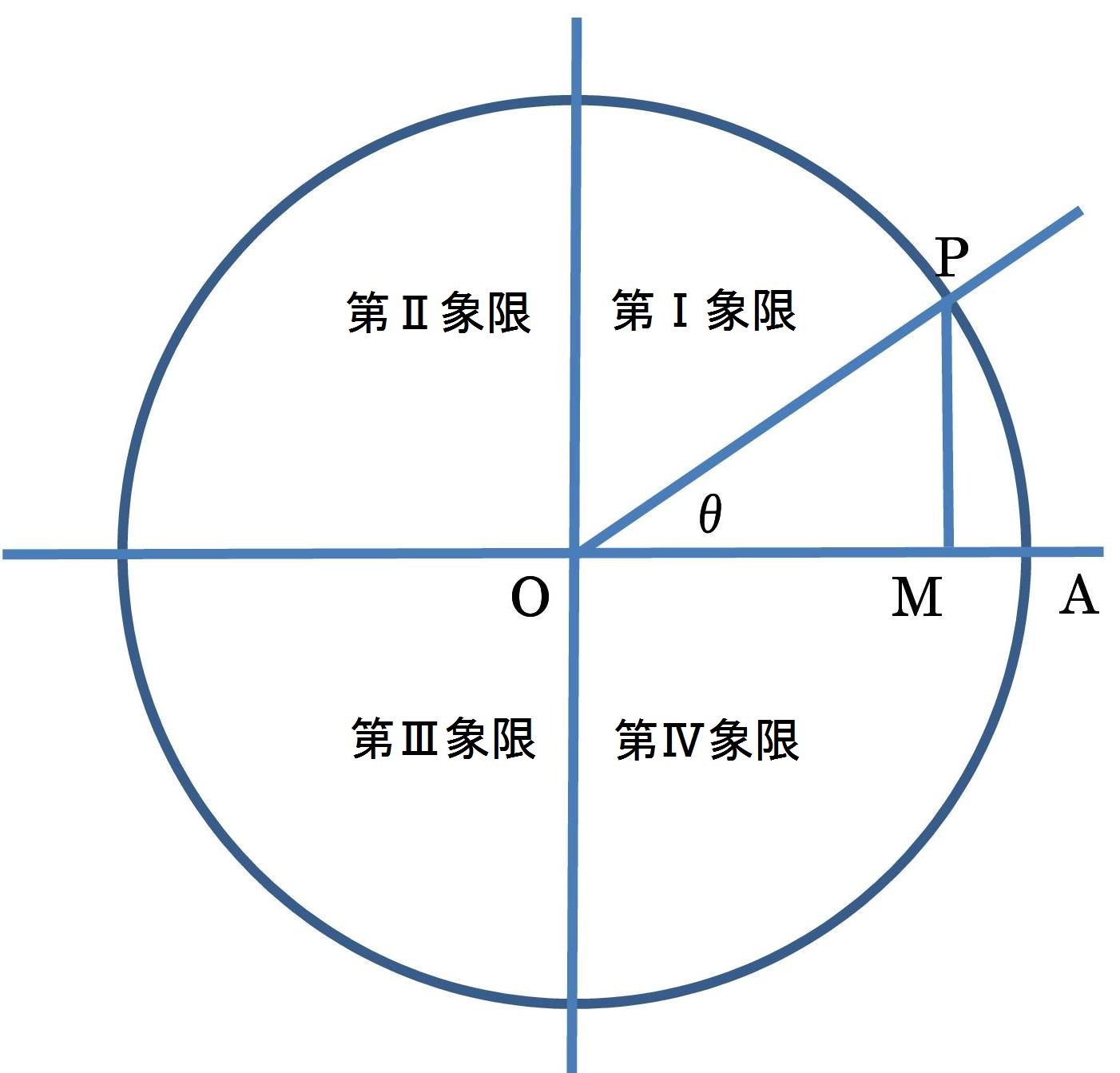
| 正弦 sinθ=MP/OP, | 余弦 cosθ=OM/OP |
| 正接 tanθ=MP/OM, | 余接 cotθ=OM/MP |
| 正割 secθ=OP/OM, | 余割 cscθ=OP/MP |
と定義される。
|