☆☆☆数学の基礎概念☆☆☆
指数関数と対数関数

−指数関数と対数関数−


１．指数関数
　ｋ個のａの積をａkと記述し、ａのｋ乗と読む。このｋを指数という。

ａk＝ ａ×ａ×ａ×・・・×ａ
ｋ個

　また、この演算では、次の指数法則が成立する。

ａmａn＝ａm+n

(ａm)n＝ａmn

(ａｂ)n＝ａnｂn

ここで、特に、ａ0＝１，ａ-m＝１／ａm と約束する。

　いま、任意の定数ａが０より大きく、ｘが−∞と＋∞の間の変数である時、次の形の指数関数を得る。

ｙ＝ａx

　もし、ａ＝ｅであれば、指数関数は、
ｙ＝ exp(ｘ)＝ｅx

となる。これは有限の極大、極小または零点を持たない最も簡単な超越関数である。 なお、関数ｙ＝ｅxの逆関数はｙ＝logｘである。




二項展開とパスカルの三角形

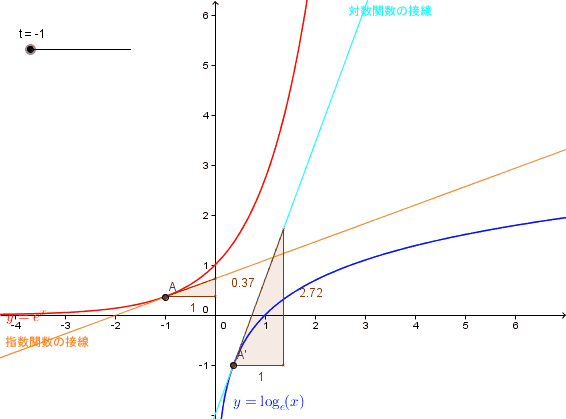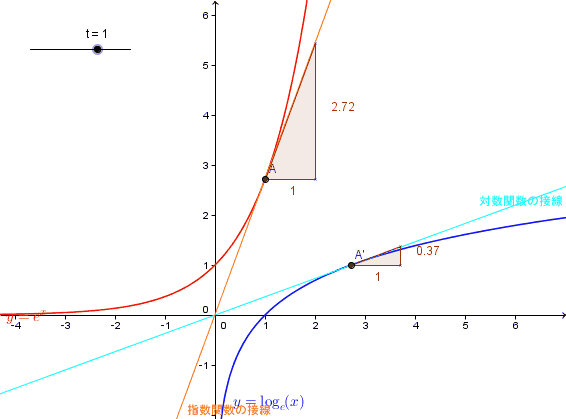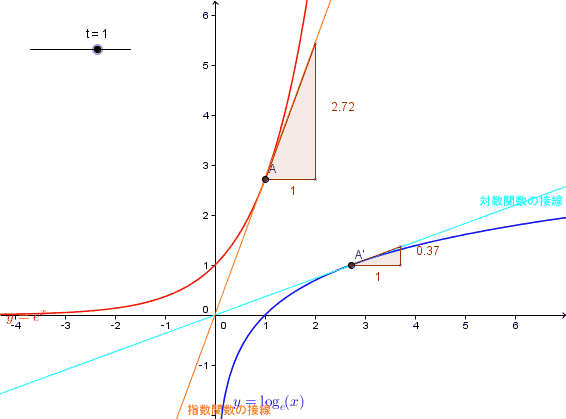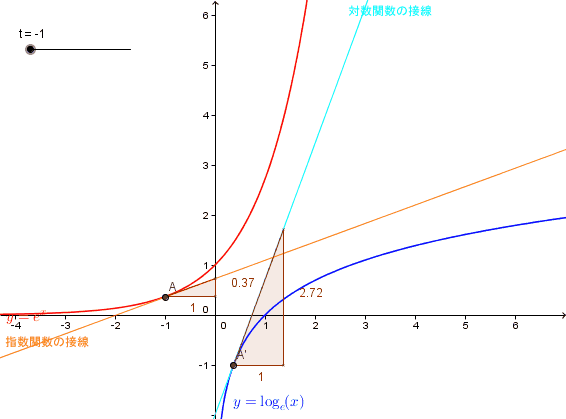
　指数法則を用いて、ａとｂの和の二乗、三乗、四乗、五乗、六乗・・・の計算をする。

(ａ＋ｂ)2＝(ａ＋ｂ)(ａ＋ｂ)＝(ａ＋ｂ)ａ＋(ａ＋ｂ)ｂ
＝ａａ＋ｂａ＋ａｂ＋ｂｂ＝ａ2＋２ａｂ＋ｂ2
(ａ＋ｂ)3＝(ａ＋ｂ)2(ａ＋ｂ)＝(ａ2＋２ａｂ＋ｂ2)(ａ＋ｂ)
＝ａ3＋３ａ2ｂ＋３ａｂ2＋ｂ3
(ａ＋ｂ)4＝ａ4＋４ａ3ｂ＋６ａ2ｂ2＋４ａｂ3＋ｂ4
(ａ＋ｂ)5＝ａ5＋５ａ4ｂ＋１０ａ3ｂ2＋１０ａ2ｂ3＋５ａｂ4＋ｂ5
(ａ＋ｂ)6＝ａ6＋６ａ5ｂ＋１５ａ4ｂ2＋２０ａ3ｂ3＋１５ａ2ｂ4＋６ａｂ5＋ｂ6
・
・
・

　これら一連の計算は二項展開と呼ばれ、各項の係数を二項係数という。なお、この二項係数は「パスカルの三角形」を構成する。

「パスカルの三角形」(１０段の場合)



２．対数関数
　指数関数 ａc＝ｂ において、ｃ＝logaｂと記述し、 log のことを対数と言う。ここで、ａは底、ｂは真数と呼ばれる。 対数関数は、指数関数の逆関数である。つまり、対数ｎは、真数ｂを得るための底ａを累乗すべき指数ｎである。 なお、底ａは ａ＞０かつａ≠−１ でなければならない。また、真数ｂは ｂ＞０ の時に、対数関数が定義される。 これらは、対数関数の「底の条件」および「真数の条件」と呼ばれる。

logaｂ＝ｎ

ａn＝ｂ

　真数１の対数は、すべての場合に０である。つまり、すべてのａに対して、

ａ0＝１

であるから、

loga＝０

　もしも、底ａと真数ｂが等しく、ａ＝ｂならば、対数ｎは１である。つまり、すべてのａに対して、

ａ1＝ａ

であるから、

logaａ＝１


−対数計算の公式−
loga(ｘ・ｙ)＝logaｘ＋logaｙ
loga(ｘ／ｙ)＝logaｘ−logaｙ
loga(ｘy)＝ｙlogaｘ
logay√(ｘ)＝logaｘ(１／ｙ)＝(１／ｙ)logaｘ

　これらの公式は、累乗の計算規則(公式)から容易に求めることができる。

−対数計算の発展公式(参考)−
ａlogbｃ＝ｃlogbａ
logaｂ･logbｃ＝logaｃ
logaｂ･logbｃ･logcｄ＝logaｄ
logaｂ＝１／logbａ

−常用対数と自然対数−
　対数は、０および１以外の任意の正の数は、底として用いることができ、科学や工学の世界では、底ｅ＝2.71828･･･ と、それを用いて定義された自然対数（底ｅを略記して、単にlog または ln）がしばしば用いられる。

　また、計算で広く用いられる常用対数は、底10を持っており、
log10１０＝１　　　　log10０．１＝−１
log10１００＝２log10０．０１＝−２
log10１，０００＝３log10０．００１＝−３
・・
・・
・・

などの関係がある。

　なお、自然対数は、底をｅとする対数で、lnｘあるいはlogeと書き、

log10ｘ＝lnｘ／ln１０

の関係がある。ここで、ln１０＝2.302585093･････である。

以上　　

（２０１３年３月２４日）


戻る