 ☆☆☆数学の基礎概念☆☆☆
☆☆☆数学の基礎概念☆☆☆
ベクトルとマトリクス(行列)

-ベクトルとマトリクス(行列)-
それぞれの大きさだけを表すただ1つの数値の量は、スカラーまたはスカラー量と呼ばれる。例えば、線分の長さ、2直線間の角度、三角形の面積、などはスカラーまたはスカラー量である。
また、物理学上の物質の質量、時間、温度などは、それらを測る単位を指定すれば、それぞれの大きさを表すただ1つの数値で表現され、スカラーまたはスカラー量となる。
これに対して、幾何学上の有向(向きを持つ)線分、平行移動などは、その大きさを表す数値だけでなく、その向きを指定しなければ、その性質を完全に表現することができない。
物理学上では、速度、加速度、力など、その大きさを表す数値と向きを指定しなければ、完全に表現することができない。
これらは、スカラーまたはスカラー量と異なるしかるべき演算規則に従わなければならない。数値と向きを伴うこれらの量は、ベクトルまたはベクトル量と呼ばれる。
マトリクス(行列)とは、行と列に要素(成分)を持つ量のことである。ベクトルもマトリクスの仲間、一列しかないマトリクス、あるいは一行しかないマトリクスのことである。
したがって、一列しかないマトリクスは列ベクトル、一行しかないマトリクスは行ベクトルとも呼ばれる。また、要素(成分)が一つしかないベクトル(あるいはマトリクス)は、スカラーと呼ばれている。
マトリクスもベクトルも複数の数値を表したもの、重要なのは、マトリクスとベクトル、あるいはマトリクスとマトリクスの演算則にある。
そこには、一般の代数学で用いる演算則と異なるルールに基づく、合理的な規則性が存在する。そのルールと規則性を正しく理解することで、
複雑な仕組みや現象を単なる連立方程式に置き換えることができ、数学的な手法を自然現象や社会現象を解読することに用いることも可能になる。
1.ベクトル
空間に2つの点、PとQがある時、PからQに至る有向線分をベクトルという。ベクトルはPからQに至る矢印を持つ線分で表し、点Pをベクトルの始点、点Qをベクトルの終点という。
また、一般に、ベクトルは、a,b,u,vなど、太文字で表記される。
ベクトルvを3次元座標で考えると、その始点と終点には、座標P(x1,y1,z1)と座標Q(x2,y2,z2)が与えられる。
そして、その長さは、∣v∣と表記され、座標系に関する次の成分を持ち、
vx=x2-x1, vy=y2-y1, vz=z2-z1
ピタゴラスの定理から、次式が得られる。
∣v∣=√(vx2+vy2+vz2)
もしも、2つのベクトルu,vが等しければ、
u=v
異なるならば、
u≠v
と表記する。なお、長さが1のベクトルは単位ベクトルと呼ばれる。
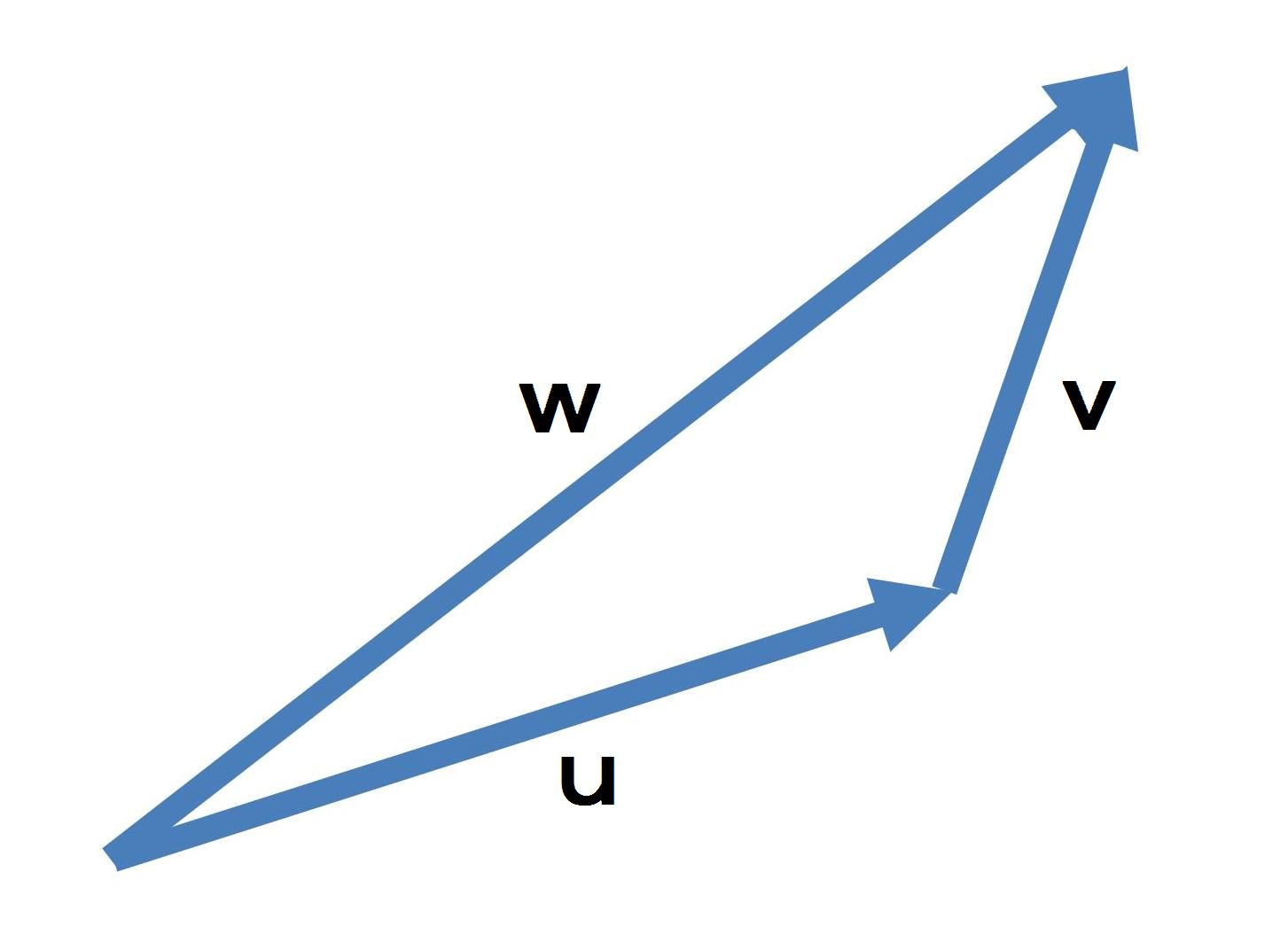
ベクトルの和は、2つのベクトルu,vが与えられた時、uの終点にvの始点を一致させ、
uの始点からvの終点に引いたベクトルwがベクトルuとvの和として定義される。
| w=u+v |
 |
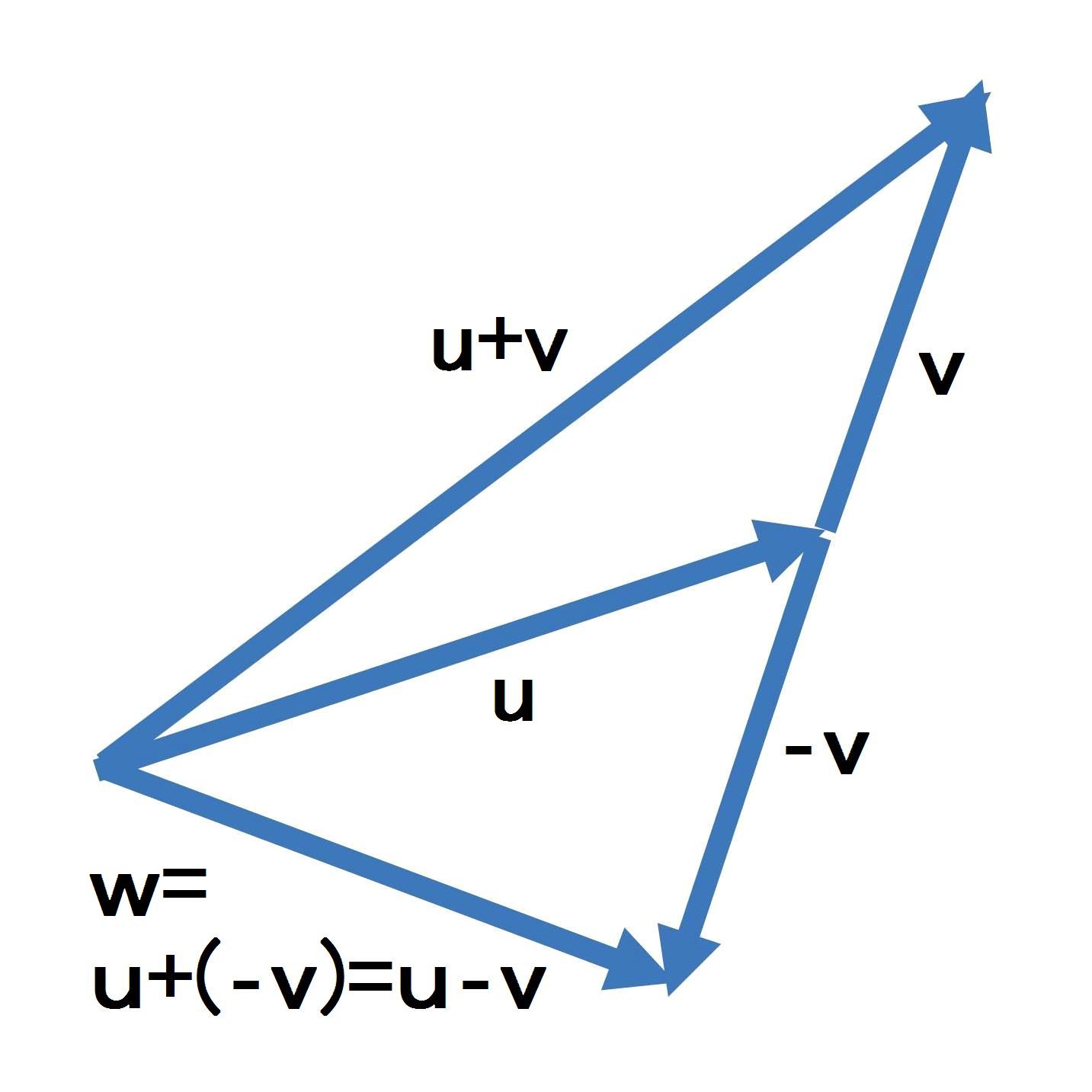
ベクトルの差は、ベクトルuとベクトルvの逆向きベクトル(-v)との和を意味し、w=u+(-v)=u-vとして定義される。
| w=u+(-v)=u-v |
 |
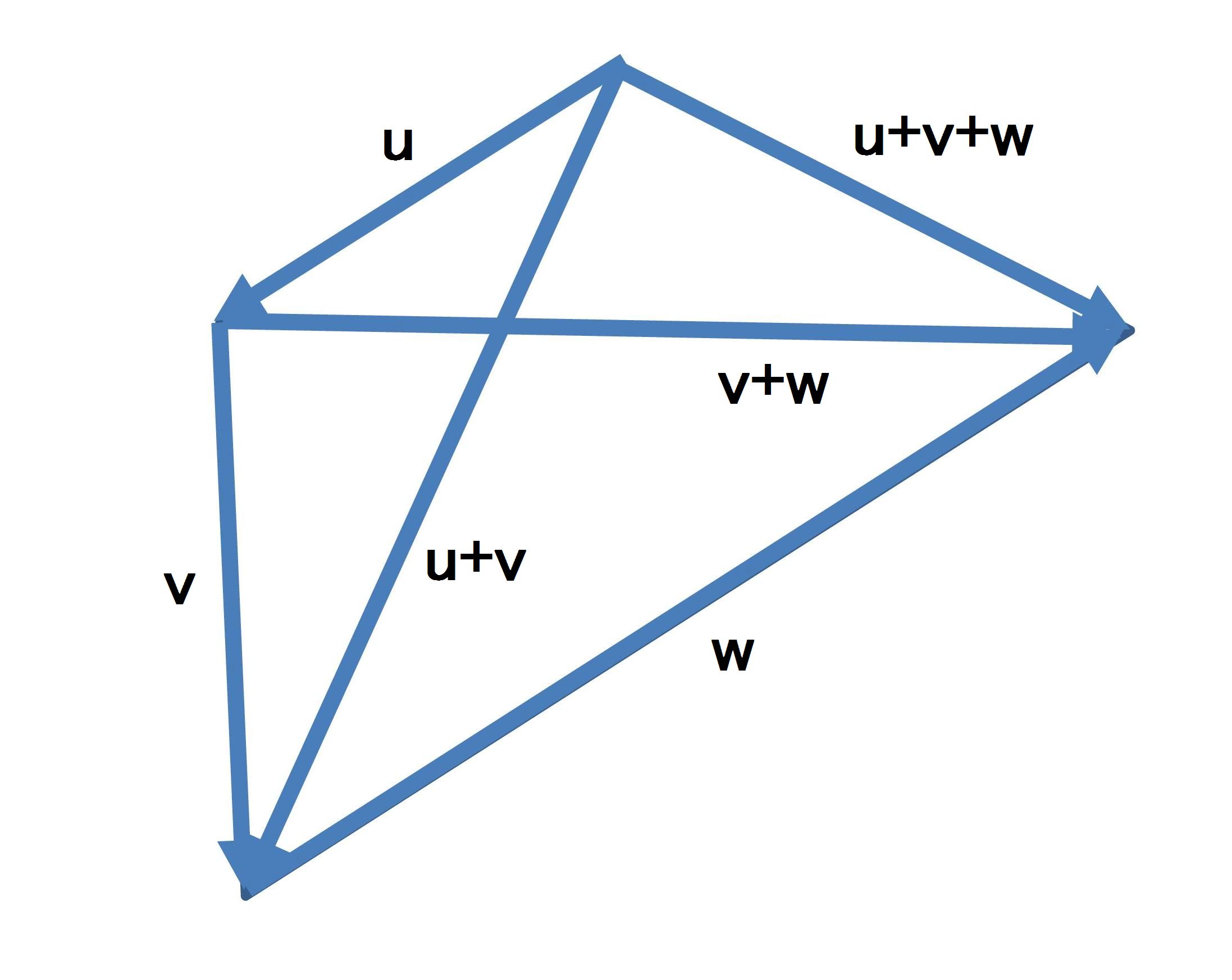
また、ベクトルの加法は、交換則と結合則が成立する。すなわち、ベクトル和wは、ベクトルvの終点にuの始点を一致させ、
vの始点からuの終点に引いたベクトルとも等しく一致する。このことから、次のベクトル和の交換則が得られる。
| u+v=v+u |
 |
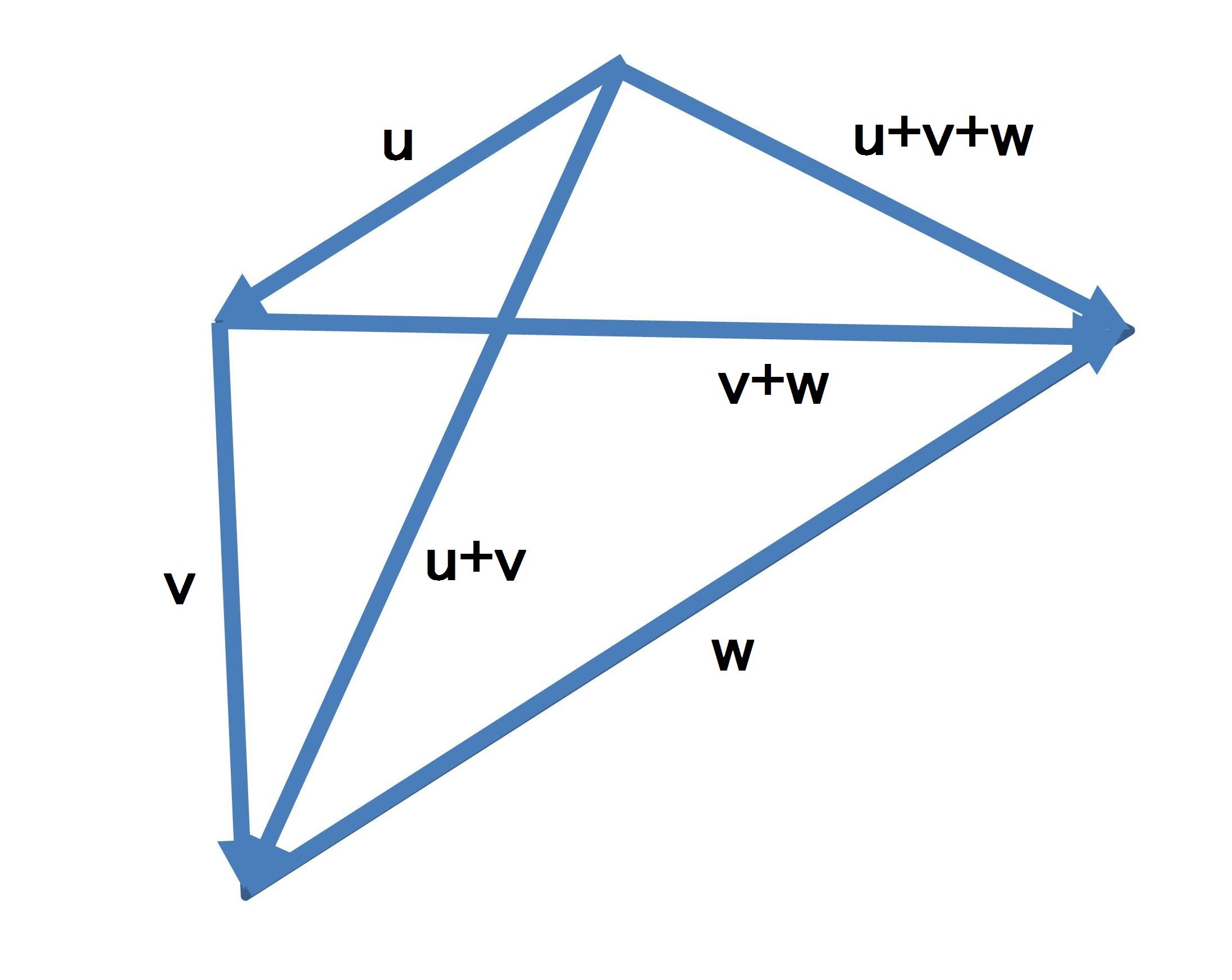
同様に、ベクトルu.v,wを考えると、次の結合則も成立する。
| u+v+w=(u+v)+w=u+(v+w) |
 |
なお、零ベクトル0を考えると、任意のベクトルuに対して、
u+0=0+u=u
が成立する。つまり、零ベクトル0は、次のように定義でき、
0=u-u
すべての要素(成分)が0で、向きを持たないベクトルとも言える。
さらに、ベクトルの和から、
u+u=2u
である。この場合、スカラーaを用いて、a=2、u+u=auとなる。スカラーaは任意の定数であり、スカラーとベクトルの関係は、次の配分則と結合則が成立する。
(a+b)u=au+bu
a(u+v)=au+av
a(bu)=(ab)u
ベクトル算法の計算規則
| 交換則 | u+v=v+u |
| 結合則 | u+v+w=(u+v)+w=u+(v+w) |
| 配分則 | (a+b)u=au+bu |
| 配分則 | a(u+v)=au+av |
| 結合則 | a(bu)=(ab)u |
ベクトルの内積と外積
向きの異なる2つのベクトルとベクトルとの掛け算はできない。そこで、ベクトルの向きを考慮してベクトルの掛け算(積)ができるようにした計算規則が考えられた。それがベクトルの内積と外積である。
ベクトルの内積
ベクトルの内積は、スカラー積とも呼ばれ、その定義式は、同じ始点を持つ2つのベクトルuとvとのなす角θとすると、次式で与えられる。
u・v=∣u∣∣v∣ cosθ
| u・v=∣u∣∣v∣ cosθ |
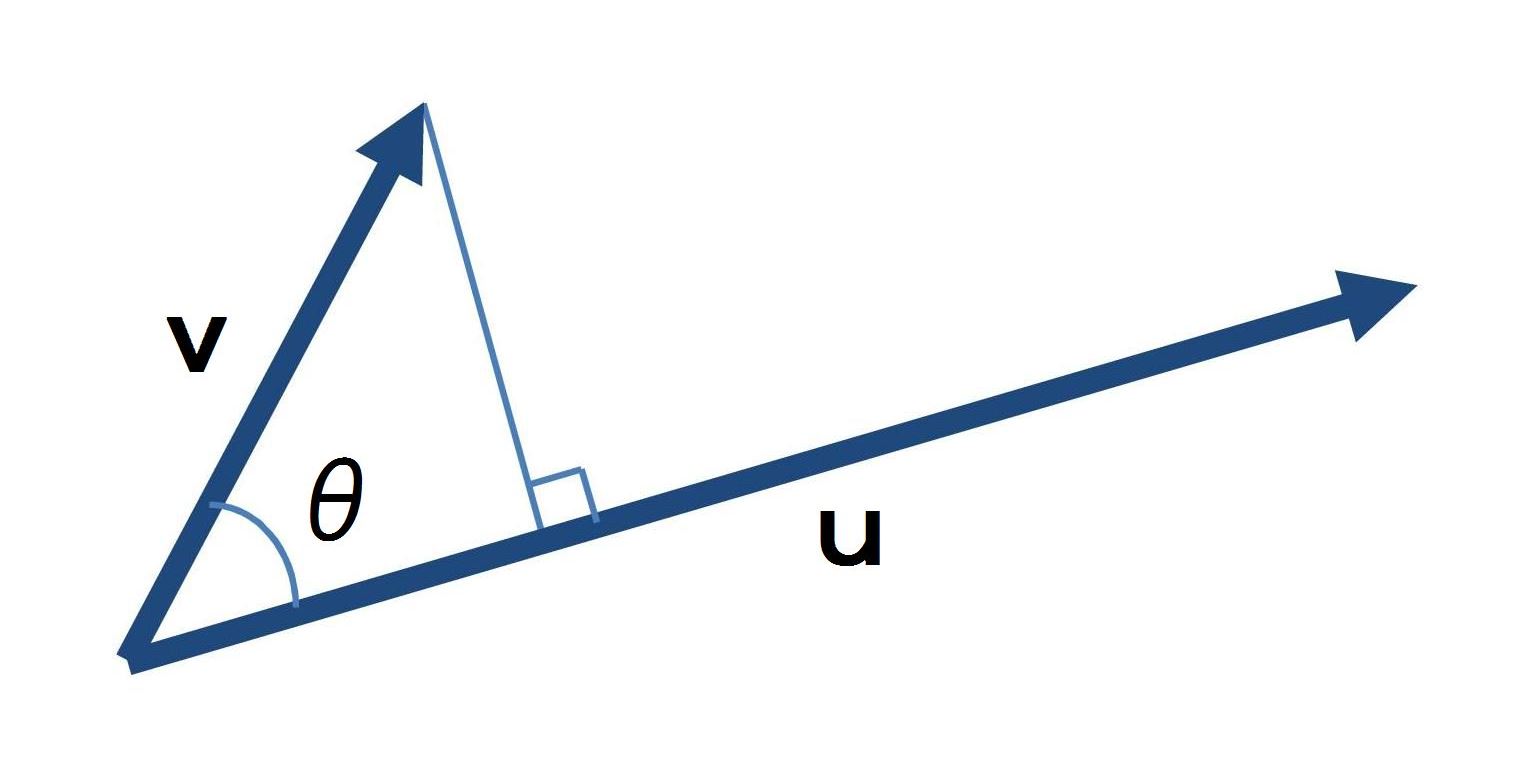 |
すなわち、ベクトルvの成分が、ベクトルuの向きと同じ方向にある時、その絶対値の掛け算(積)として、ベクトルの内積(スカラー積)が表示される。
したがって、ベクトルの内積、つまりスカラー積の値は、実数(スカラー)となる。
ベクトルの内積(スカラー積)は、交換法則が成り立ち、ベクトルの和に対して分配法則が成立する。
u・v=v・u
u・(v+w)=u・v+u・w
内積(スカラー積)の成分表示
2次元平面ベクトルの場合、
u=(ux,uy), v=(vx,vy)
u・v=uxvx+uyvy
3次元平面ベクトルの場合、
u=(ux,uy,uz), v=(vx,vy,vz)
u・v=uxvx+uyvy+uzvz
ベクトルの外積
ベクトルの外積は、ベクトル積とも呼ばれ、その定義式は、同じ始点を持つ2つのベクトルuとvとのなす角θとすると、次式で与えられる。
w=u×v
∣w∣=∣u×v∣=∣u∣∣v∣ sinθ
w=u×v
∣w∣=∣u×v∣=∣u∣∣v∣ sinθ |
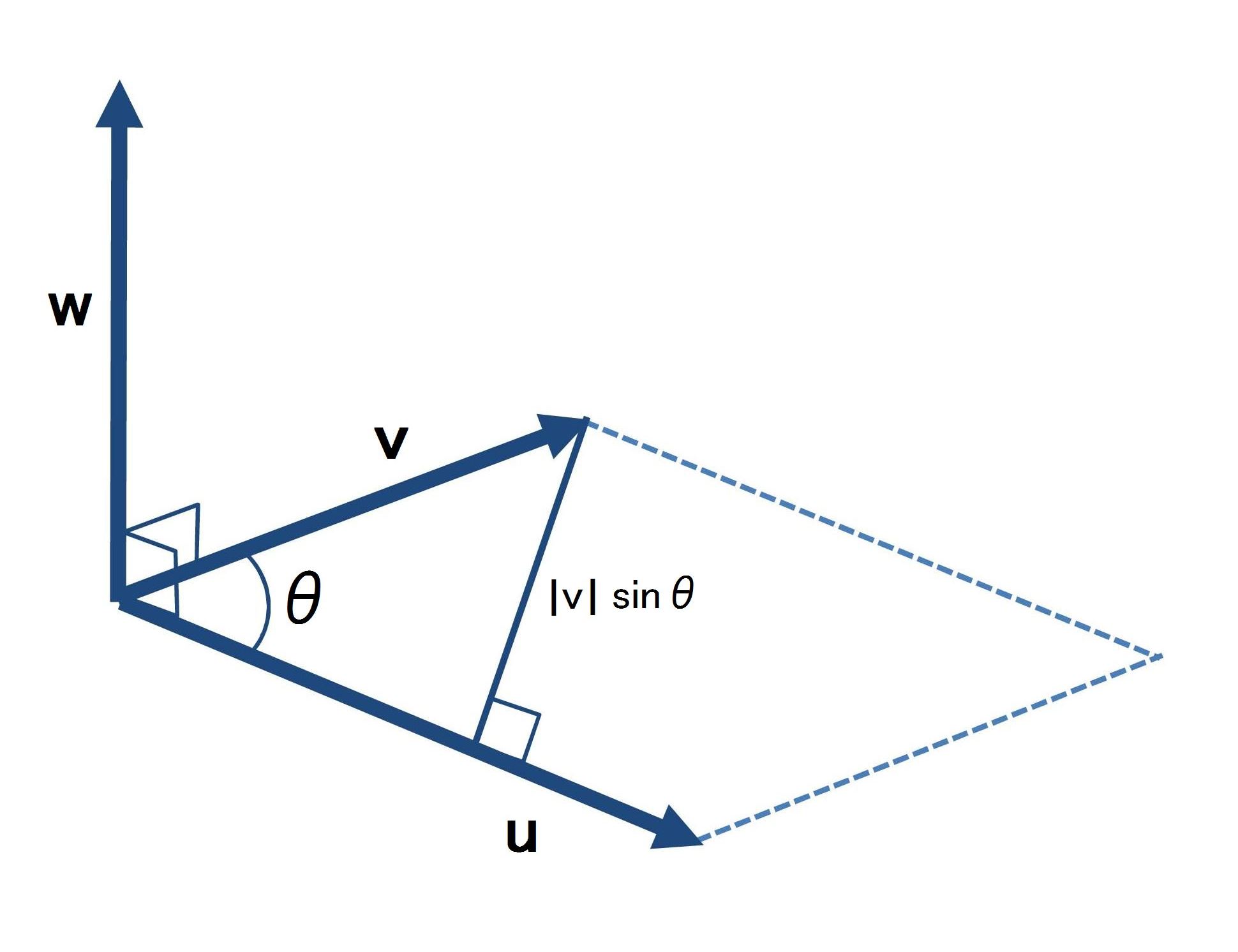 |
すなわち、ベクトルの外積(ベクトル積)は、2つのベクトルuとvが作る面積がベクトルの大きさとなり、その面積に垂直な向きを持つベクトルwで与えられる。
この場合、ベクトルの外積(ベクトル積)は、右手座標系が用いられている。
右手座標系とは、ベクトルuとvで構成するx-y平面を、右手の親指と人差指に対応付け、薬指にベクトルwの向きを与え、z軸とする直交座標系が用いられる。
したがって、ベクトルの外積(ベクトル積)は、交換法則が成立せずに、次式が成立する。
u×v=-(v×u)
一方、外積(ベクトル積)において、ベクトルの和に対しては、分配法則が成立する。
u×(v+w)=(u×v)+(u×w)
(u+v)×w=(u×w)+(v×w)
特に、一般的に、外積(ベクトル積)は、
u×(v×w)≠(u×v)×w
であることに注意すべきである。
外積(ベクトル積)の成分表示
u=(ux,uy,uz), v=(vx,vy,vz)
u×v=(uyvz-uzvx,uzvx-uxvz,uxvy-uyvx)
2.マトリックス
マトリクス(行列)は、横と縦にmn個の要素(成分)を配列したもの、要素(成分)aijは元とも呼ばれ、実数、複素数、あるいはそれらを変数とする関数のどれでもよい。
mn個の元aij (i=1,2,3,・・・,m, j=1,2,3,・・・,n)は、次の形に配列され、mn次の行列と呼ばれており、太大文字Aで代表され、次式で表示される。
| A=[Aij]= |
 | a11 | a12 | ・・・ | a1n |  |
| a21 | a22 | ・・・ | a2n |
| | ・・・ | ・・・ | |
| am1 | am2 | ・・・ | amn |
|
マトリクス(行列)は、正方の時もあれば、矩形の時もある。また、行列が1行、あるいは1列の時は、ベクトルと呼ばれ、行ベクトル、あるいは列ベクトルを構成する。
マトリクス(行列)Aの行と列を入れ替えたマトリクス(行列)は、転置行列と呼ばれ、ATと表示する。
| AT= |
 | a11 | a21 | ・・・ | am1 |  |
| a12 | a22 | ・・・ | an2 |
| | ・・・ | ・・・ | |
| a1n | a2n | ・・・ | amn |
|
マトリクス(行列)の計算
行列の和と差は、対応する位置の数の加減となる。したがって、行数と列数が同じ行列同士でなければ、足し算、引き算ができない。
マトリクス(行列)が2行2列の場合の計算事例
 | a11 | a12 |  |
| a21 | a22 |
|
+ |
 | b11 | b12 |  |
| b21 | b22 |
|
= |
 | a11+b11 | a12+b12 |  |
| a21+b21 | a22+b22 |
|
 | a11 | a12 |  |
| a21 | a22 |
|
- |
 | b11 | b12 |  |
| b21 | b22 |
|
= |
 | a11-b11 | a12+b12 |  |
| a21-b21 | a22+b22 |
|
| α |
 | a11 | a12 |  |
| a21 | a22 |
|
= |
 | α a11 | α a12 |  |
| α a21 | α a22 |
|
 | a11 | a12 |  |
| a21 | a22 |
|
× |
 | b11 | b12 |  |
| b21 | b22 |
|
= |
 | a11b11+a12b21 | a11b12+a12b22 |  |
| a21b11+a22b21 | a21b12+a22b22 |
|
 | a11 | a12 | a13 |  |
| a21 | a22 | a23 |
|
× |
 | b11 | b12 |  |
| b21 | b22 |
| b31 | b32 |
|
= |
 | a11b11+a12b21+a13b31 | | a11b12+a12b22+a13b32 |  |
| a21b11+a22b21+a22b21 | | a21b12+a22b22+a23b31 |
|
マトリクス(行列)算法の計算規則
| 交換則 | A+B=B+A |
| 結合則 | A+B+C=(A+B)+C=A+(B+C) |
| 配分則 | (a+b)A=aA+bA |
| 配分則 | a(A+B)=aA+aB |
| 結合則 | a(bA)=(ab)A |
| 積の交換則 | AB≠BA(行列の積は不可換) |
| 積の結合則 | ABC=(AB)C=A(BC) |
| 積の結合則 | A(B+C)=AB+AC) |
| 積の結合則 | (A+B)C=AC+BC |
行列のべぎ乗 A1=A, A2=AA, A3=A2A,・・・
単位行列とゼロ行列
正方行列Aの主対角線上の上側と下側の要素(成分)のすべてが0の時、すなわちj≠kならばajk=0である時、正方行列Aは対角行列と呼ばれる。
この対角行列の主対角線上の要素(成分)のすべてが1の時、これを単位行列Iという。また、すべての要素(成分)が0の時、これをゼロ行列0という。
| I= |
 | 1 | 0 | 0 |  |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
|
|
0= |
 | 0 | 0 | 0 |  |
| 0 | 0 | 0 |
| 0 | 0 | 0 |
|
単位行列とゼロ行列は、任意の正方行列Aに対して、次の計算規則が成立する。
| ゼロ行列の計算規則 | A+0=0+A=A |
| ゼロ行列の計算規則 | A+(-A)=(-A)+A=A-A=0 |
| ゼロ行列の計算規則 | 0A=A0=0 |
| 単位行列の計算規則 | IA=AI=I |
| 単位行列の計算規則 | A0=I |
逆行列と正則行列
正方行列Aに対して、AB=BA=Iとなるような正方行列Bが存在する時、BをAの逆行列と呼び、A-1で表示する。
この時、正方行列Aは正則であるとされ、Aを正則行列という。つまり、正則行列とは、逆行列が存在する行列のことである。
n次の正則行列は、次の計算規則が成立する。
| 正則行列の計算規則 | ∣A-1∣=∣A∣-1 |
| 正則行列の計算規則 | (A-1)-1=A |
| 正則行列の計算規則 | (AB)-1=A-1B-1 |
正方行列と行列式
行の数と列の数が等しい行列、つまり、n=mの行列をn次の正方行列と呼び、nはその次数である。行列式は、n次の正方行列Aに対して、
| detA=∣A∣= |
 | a11 | a12 | ・・・ | a1n |  |
| a21 | a22 | ・・・ | a2n |
| | ・・・ | ・・・ | |
| an1 | an2 | ・・・ | ann |
|
と記述する。この場合、2次の行列式は、文字記号を変更して表示すると、
 | a1 | b1 |  |
| a2 | b2 |
|
=a1b2-a2b1 |
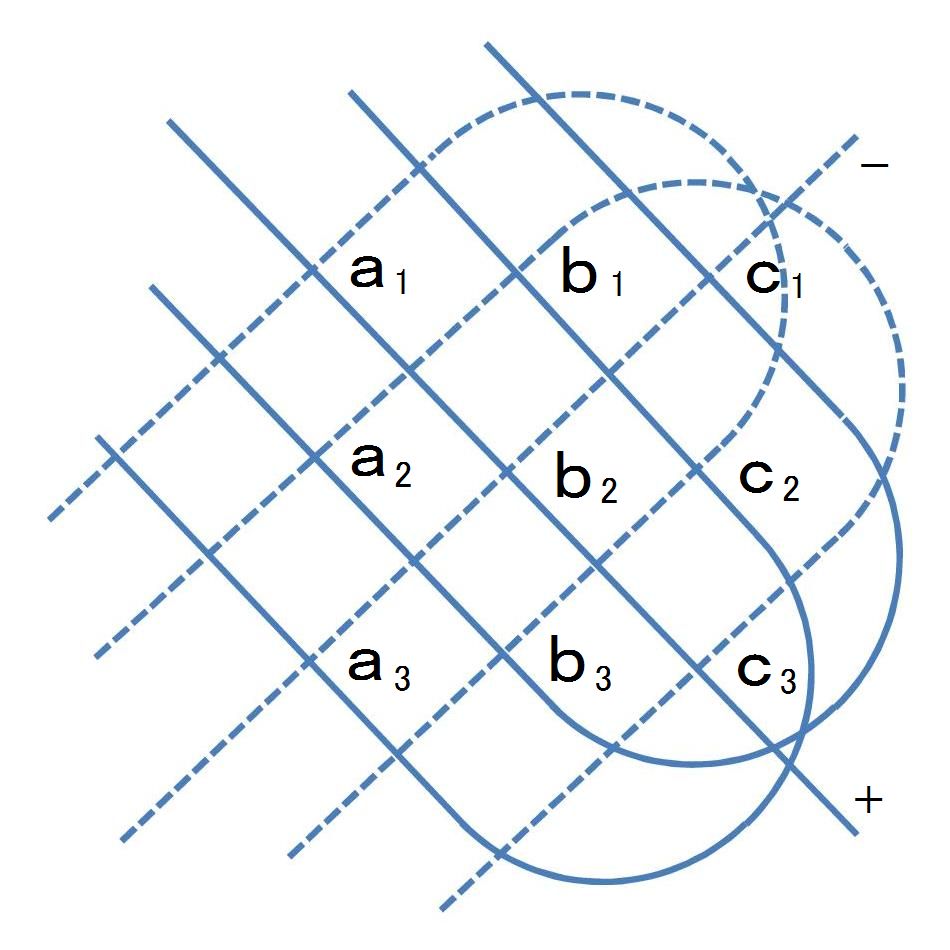
と展開される。3次の行列式の場合は、下記のように展開される。
展開の方法は、下図のように、実線上の元(要素、成分)、a1b2c3、a2b3c1、a3b1c2
には+の符号を付与し、破線上の元(要素、成分)、a1b3c2、a2b1c3、a3b2c1
には-の符号を付与する。
 | a1 | b1 | c1 |  |
| a2 | b2 | c2 |
| a3 | b3 | c3 |
|
=a1b2c3+a2b3c1+a3b1c2-a1b3c2-a2b1c3-a3b2c1 |
行列式の展開
行列式において、1つの要素を含む行と列を除いた残りの要素で作った行列式はその要素の小行列式という。
また、サイズn×nの正方行列Aにおいて、第i行と第j列の成分をすべて0で置き換え、
ただし第 (i,j) 成分だけは1で置き換えて得られる行列の行列式|A|の第(i,j)余因子という。
この場合、余因子は、第i行と第j列を消去して得られるサイズ(n-1)×(n-1)の行列の行列式に(-1)i+jを掛けたものに等しい。
行列式|A|は、余因子を使用して、展開することができる。例えば、3次の行列式を余因子展開すると、
 |
a1 | b1 | c1 |
 |
| a2 | b2 | c2 |
| a3 | b3 | c3 |
|
=a1 |
 |
b2 | c2 |
 |
| b3 | c3 |
|
-b1 |
 |
a2 | c2 |
 |
| a3 | c3 |
|
+c1 |
 |
a2 | b2 |
 |
| a3 | b3 |
|
=a1b2c3+a2b3c1+a3b1c2-a1b3c2-a2b1c3-a3b2c1
となる。
連立1次方程式のマトリクス(行列)表示と行列式
連立1次方程式はマトリクス(行列)を用いて表示することができる。また、その解は行列式で与えられる。2元1次の連立方程式の場合、
 |
a1x1+b1x2=y1 |
| a2x1+b2x2=y2 |
|
であり、その解は、a1b2-a2b1≠0ならば、すなわち不能や不定でなければ、行列式で表示すると、
となる。3元1次の連立方程式の場合は、
 |
a1x1+b1x2+c1x3=y1 |
| a2x1+b2x2+c2x3=y2 |
| a3x1+b3x2+c3x3=y3 |
|
 | a1 | b1 | c1 |  |
| a2 | b2 | c2 |
| a3 | b3 | c3 |
|
 | x1 |  |
| x2 |
| x3 |
|
= |
 | y1 |  |
| y2 |
| y3 |
|
となり、その解は、それが不能や不定でなければ、
| x1= |
 | y1 | b1 | c1 |  |
| y2 | b2 | c2 |
| y3 | b3 | c3 |
|
 |
 | a1 | b1 | c1 |  |
| a2 | b2 | c2 |
| a3 | b3 | c3 |
|
| x2= |
 | a1 | y1 | c1 |  |
| a2 | y2 | c2 |
| a3 | y3 | c3 |
|
 |
 | a1 | b1 | c1 |  |
| a2 | b2 | c2 |
| a3 | b3 | c3 |
|
| x3= |
 | a1 | b1 | y1 |  |
| a2 | b2 | y2 |
| a3 | b3 | y3 |
|
 |
 | a1 | b1 | c1 |  |
| a2 | b2 | c2 |
| a3 | b3 | c3 |
|
|
|
で与えられる。いずれにしても、連立1次方程式は、マトリクス(行列)表示を用いて、
Ax=y
となる。ここで、Aは、連立1次方程式の係数をマトリクス(行列)表示したものであり、xは未知数となる1列の列ベクトルである。yは定数項を意味する1列の列ベクトルである。
連立1次方程式の解法(ガウスの消去法、掃き出し法)
最初に、具体的な数値事例に基づき、次の3元連立1次方程式Ax=yについて、ガウスの消去法、すなわち掃き出し法を使って解いてみる。
ガウスの消去法(掃き出し法)とは、ある式を何倍かして、他の式から引く等の処理を施して、1つの式に含まれる変数の数を減らしながら解く方法である。
与えられた3元連立1次方程式は、
 |
2x1- x2+2x3= 2 |
| x1+10x2-3x3= 5 |
| -x1+ x2+ x3=-3 |
とする。これは次のようにマトリクス(行列)で表示される。
 |
2 | -1 | 2 |
 |
| 1 | 10 | -3 |
| -1 | 1 | 1 |
|
 |
x1 |
 |
| x2 |
| x3 |
|
= |
 |
2 |
 |
| 5 |
| -3 |
|
この方程式の解は、マトリクス(行列)表示で、次のようになる。
 |
1 | 0 | 0 |
 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
|
 |
x1 |
 |
| x2 |
| x3 |
|
= |
 |
2 |
 |
| 0 |
| -1 |
|
x1=2, x2=0, x3=-1
次に、掃き出し法の具体的な手順を示す。最初に、方程式の左辺の係数と右辺の定数項について、次のような拡張されたマトリクス(行列)で表示する。
 |
2 | -1 | 2 | 2 |
 |
| 1 | 10 | -3 | 5 |
| -1 | 1 | 1 | -3 |
① 連立方程式は行を入れ替えても影響はない。そこで、1行1列目を1(単位数)にするため、1行目を2行目と入れ替える。つまり、1番目の式と2番目の式を入れ替える。
 |
1 | 10 | -3 | 5 |
 |
| 2 | -1 | 2 | 2 |
| -1 | 1 | 1 | -3 |
② 1行目の2倍を2行目から引く。
 |
1 | 10 | -3 | 5 |
 |
| 0 | -21 | 8 | -8 |
| -1 | 1 | 1 | -3 |
③ 1行目を3行目に加える。
 |
1 | 10 | -3 | 5 |
 |
| 0 | -21 | 8 | -8 |
| 0 | 11 | -2 | 2 |
④ 3行目の2倍を2行目に加える。
 |
1 | 10 | -3 | 5 |
 |
| 0 | 1 | 4 | -4 |
| 0 | 11 | -2 | 2 |
⑤ 2行目の11倍を3行目から引く。
 |
1 | 10 | -3 | 5 |
 |
| 0 | 1 | 4 | -4 |
| 0 | 0 | -46 | 46 |
⑥ 3行目を-46で割る。
 |
1 | 10 | -3 | 5 |
 |
| 0 | 1 | 4 | -4 |
| 0 | 0 | 1 | -1 |
⑦ 2行目の10倍を1行目から引く。
 |
1 | 0 | -43 | 45 |
 |
| 0 | 1 | 4 | -4 |
| 0 | 0 | 1 | -1 |
⑧ 3行目の43倍を1行目に加える。
 |
1 | 0 | 0 | 2 |
 |
| 0 | 1 | 4 | -4 |
| 0 | 0 | 1 | -1 |
⑨ 3行目の4倍を2行目から引く。
 |
1 | 0 | 0 | 2 |
 |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | -1 |
⑩ 以上、4列目が与えられた方程式の解になる。
以上
(2013年3月24日)
戻る
|






